
제 14회는 2002년 8월 18일부터 25일까지 우리나라 용인(경희대학교 캠퍼스)에서 열렸다. 우리나라 지명이 들어 있는 영어 문제를 번역하는 느낌은 참으로 이색적이었다. 이번 대회에서 쓰인 하드웨어 환경은 램 256MB, 1.7GHz인 펜티엄 4였다. 한편, 소프트웨어 환경으로는 작년에 처음으로 도입된 GNU C/C++과 파스칼이 IOI 공식 언어로 쓰였다.
프로그램 채점 기술의 발달로, 답안 프로그램의 입출력을 파일로 하던 모습이 앞으로 완전히 사라질 듯 하다. 작년에 많았던 인터랙티브 문제가 하나로 줄어들고, 프로그램을 제출하는 게 아니라 출력 파일만 제출하는 문제가 작년과 마찬가지로 올해에도 나와서 흥미롭다. 3번을 제외하고는 모두 부분 점수가 없는 문제이며, 문제들의 절반인 세 문제가 숫자 하나만 달랑 출력하면 되는 문제라는 것도 인상적이다.
우리나라는 이 대회에서 금메달 세 개, 동메달 한 개로 역대 최고 성적인 준우승(2위)을 차지했다. 월드컵과 더불어 올해의 통쾌한 소식이 아닐 수 없다. 600점 만점에 금메달 입상자의 최고 점수는 510점, 동메달 입상자의 최저 점수는 135점이었다.
원문이 있는 곳: http://olympiads.win.tue.nl/ioi/ioi2002/contest/index.html
한국에서는 청개구리들이 부리는 말썽이 가히 믿기 어려울 정도이다. 그도 그럴 것이, 청개구리들은 여러분이 돌보고 있는 논 위를 밤 사이에 마구 뛰어 다니면서 벼들을 쓰러뜨리기 때문이다. 아침이 되어, 쓰러진 벼들을 파악한 당신은 가장 큰 해를 끼친 청개구리가 남긴 발자취를 파악하고 싶어한다. 청개구리는 논을 언제나 일직선으로 쭉 뛰어가며, 한 번에 뛰는 간격도 언제나 같다.

논은, 그림 1처럼 모눈의 교점들에 벼가 심어져 있는 구조를 하고 있다. 그리고 문제의 청개구리들은 논 밖에서 논으로 들어와, 일직선으로 팔짝팔짝 뛰어 정확하게 벼만 짓밟고 반대편 논 밖으로 나간다. 그림 2를 참고하라.
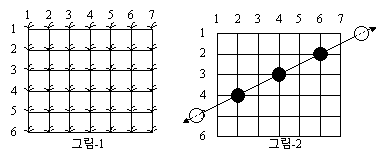
그림 3처럼, 여러 청개구리들이 제각기 다른 방향에서부터 논으로 들어와 서로 다른 방향으로 뛰어갈 수 있다. 그리고 개구리에게 밟힌 벼는 쓰러진다. 여러 개구리에게 여러 번 밟히는 벼도 있다. 하지만, 개구리들이 지나간다고 자신의 경로가 그림 3처럼 직선으로 남는 것은 아니다. 우리가 아침이 되어 확인할 수 있는 것은 그림 4처럼, 쓰러진 벼들 뿐이다.
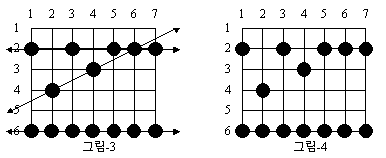
그림 4를 보면, 개구리들이 몇 마리가 와서 어느 방향으로 어느 간격으로 벼를 밟고 갔는지 그 경로를 재현할 수 있다. 단, 벼를 세 포기 이상 밟은 개구리의 경로만 생각하기로 한다. 그리고 이것을 개구리 경로라고 편의상 일컫겠다. 그렇다면, 그림 4의 상황이라면 그림 3과 같은 세 개의 개구리 경로가 있다고 말할 수 있다. (물론 다른 가짓수도 있을 수 있다.)
한편, 첫째 칸에서 수직으로 내려가는 경로는 간격이 4인 개구리 경로일 수도 있지만, 이 경로의 영향을 받은 벼는 두 포기밖에 없기 때문에 고려하지 않는다. 그리고 둘째 줄 셋째 칸(2, 3), 셋째 줄 넷째 칸(3, 4), 여섯째 줄 일곱째(6, 7) 칸을 지나는 경로는 일직선이고 벼가 세 포기가 속해 있지만, 간격이 일정하지 않기 때문에 개구리 경로로 인정하지 않는다.
어떤 개구리 경로에 속하는 선에는, 다른 개구리 경로에 속하는 벼가 있을 수 있다. 예를 들어 위 그림에서 (2, 1), (2, 3), (2, 5), (2, 7)은 개구리 경로인데, 이 선 안에는 (2, 6)처럼 다른 개구리에게 밟힌 벼가 또 있다. 그리고 사실은, 쓰러진 벼 중에는 어느 개구리 경로에도 속하지 않은 벼도 있을 수 있다. 개구리에게 밟힌 벼라고 해서, 모두 다 조건을 만족하는 '개구리 경로'에 속하는 것이 아니기 때문이다.
이번 문제는, 가능한 개구리 경로를 모두 조사하여, 벼를 가장 많이 밟았다고 결론지을 수 있는 개구리 경로를 찾아, 그 경로가 지나게 되는 벼 포기의 수를 출력하는 것이다. 그림 4의 경우, 정답은 7이다. 여섯째 줄부터 가로로 벼 일곱 포기를 모두 밟는 경로가 있기 때문이다.
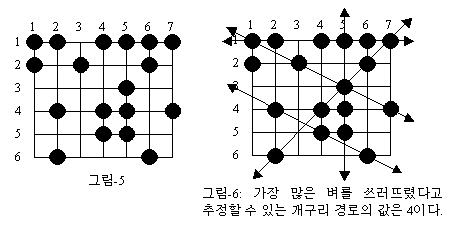
표준 입력 스트림에서 데이터를 읽어들인다. 첫째 줄에는 정수 R과 C가 있다. 각각 논의 크기인 줄 수와 칸 수를 뜻한다. 1≤R, C≤5000이다. 그리고 둘째 줄에는 개구리에게 밟힌 적이 있는 벼 포기의 수 N이 있다. (3≤N≤5000) 그리고 다음 N 줄에는 밟힌 벼의 좌표인 정수 두 개가 뒤따른다. 처음 것이 줄(세로) 좌표이고 나중 것이 칸(가로) 좌표이다. (1≤줄 좌표≤R, 1≤칸 좌표≤C) 두 정수는 공백 한 칸으로 구분된다. 여러 개구리에게 밟혔더라도 벼 한 곳의 좌표는 한 번만 나온다.
표준 출력 스트림으로 답을 출력한다. 가장 많은 벼를 쓰러뜨렸다고 말할 수 있는 개구리 경로가 쓰러뜨린 벼의 포깃수를 한 줄에다 출력한다. 만약 개구리 경로를 하나도 발견하지 못했다면 그냥 0을 출력한다.
입력 출력
6 7 7
14
2 1
6 6
4 2
2 5
2 6
2 7
3 4
6 1
6 2
2 3
6 3
6 4
6 5
6 7
 입력
출력
입력
출력
6 7 4
18
1 1
6 2
3 5
1 5
4 7
1 2
1 4
1 6
1 7
2 1
2 3
2 6
4 2
4 4
4 5
5 4
5 5
6 6
답안 프로그램이 제한 시간 내에 입력 자료에 대한 맞는 답을 출력하면 만점을 받고, 그렇지 않으면 0점을 받는다. 이 문제는 25개의 입력 데이터로 채점을 받으며, 한 데이터 당 만점은 4점으로 최대 100점을 받게 된다. 한 데이터 당 시간 제한은 2초이며, 메모리 제한은 64MB이다.
유토피아라는 아름다운 나라가 있다. 하지만 이 나라는 한때 전쟁으로 초토화되었고, 교전이 끝나자 국토는 수평선과 수직선을 경계로 네 개의 지방으로 분열되었다. 이 두 경계선의 교점은 (0, 0)점으로 알려졌다. 네 지방 사람들 모두 자기 지방에 유토피아라는 이름을 붙일 것을 고집했지만, 시간이 흐르면서 이들은 각각 제 1 유토피아(북동), 제 2 유토피아(북서), 제 3 유토피아(남서), 제 4 유토피아(남동)로 불리게 되었다. 그리고 이들 땅의 한 지점을 가리킬 때는 항상 (0, 0)점에서 동쪽으로 떨어진 거리와 북쪽으로 떨어진 거리를 나란히 적음으로써 그 위치를 나타내게 되었다. 한 마디로, 점들이 직교 좌표계에 있고, 제 1~4유토피아는 제 1~4 사분면이라고 보면 된다. 예를 들어 제 2 유토피아에 있는 지점은 (음수, 양수)쌍이 되며, 제 3 유토피아의 지점은 (음수, 음수)쌍이 된다. 제 4 유토피아의 지점은 (양수, 음수)쌍이 되며, 제 1 유토피아의 지점은 (양수, 양수)쌍으로 이루어지는 것이다.

각각의 유토피아에 사는 시민들은 경계선 너머 다른 유토피아로 자유롭게 드나들지 못했다. 하지만 다행히도 유토피아 출신의 한 총명한 IOI 참가자가, 유토피아들을 마음대로 넘나들게 해 주는 순간이동 장치를 고안했다. 당신의 과제는, 그 장치를 잘 조종하여 초기에 (0, 0)점에 있는 사람을, 주문한 순서대로 유토피아 지방들을 순간이동으로 순회시키는 것이다.
주문은, 순서대로 이동할 유토피아의 번호를 가리키는 N개의 정수로 되어 있다. (따라서 각 정수의 값은 1, 2, 3, 4 중 하나이다.) 같은 유토피아에 두 번 이상 가라는 주문도 당연히 올 수 있다. 지정된 유토피아 안의 어떤 점에다 사람을 전송시켜 놓아도 좋다. (예를 들어, 이번 차례에 1사분면으로 사람을 옮겨야 한다면 (1, 1)이든 (100, 1)이든 상관없다는 뜻.) 하지만 어떤 경우든 사람을 경계선 위로 옮겨서는 안 된다. ((0, y), (x, 0) 같은)
기기를 조종하는 방법은 다음과 같다. 2*N개의 제어 숫자가 딸려 온다. 이 숫자들은 양수이며 값이 모두 서로 다르다. 그래서 여기서 아무 숫자나 두 개씩 따 온다. 그리고 거기에 필요에 따라 양이나 음의 부호를 붙인다. 예를 들어 따온 두 숫자가 u, v라면, 사람의 현재 위치 (x, y)에다가 (+u, +v), (+u, -v), (-u, +v), (-u, -v) 중 적당한 값을 더한다. 그러면 사람은 그 위치로 순간이동된다. 모든 제어 숫자를 한 번씩만 써야 한다.
예를 들어, 순간이동 장치에 7, 5, 6, 1, 3, 2, 4, 8이라는 제어 숫자가 있고, 사람을 4, 1, 2, 1번 유토피아로 차례대로 옮겨라는 주문이 들어왔다고 치자. 그래서 제어 숫자를 바탕으로 (+7,-1), (-5,+2), (-4,+3), (+8,+6)의 순서대로 사람을 옮기면, 초기에 (0, 0)점에 있던 사람은 각각 (7,-1), (2,1), (-2,4), (6,10) 위치에 있게 되어 제 4, 제 1, 제 2, 제 1 유토피아를 차례대로 순회하게 된다.
2*N개의 제어 숫자와 N개의 주문 번호를 입력받아, (0, 0)점에 있는 사람을 주문대로 유토피아 지방을 모두 순회할 수 있도록 순간이동 장치를 조종하는 프로그램을 작성하시오.
표준 입력 스트림에서 데이터를 읽어들인다. 첫 줄에는 양수 N(1≤N≤10000)이 있다. 다음 줄에는 2N개의 서로 다른 제어 숫자가 공백 한 칸 간격을 두고 있다. (1≤제어 숫자≤100000) 그리고 마지막 줄에는 순회할 유토피아 번호의 나열이 N개 있다. (1, 2, 3, 4 중 하나)
표준 출력 스트림으로 답을 출력한다. N개의 줄에다가, 사용할 제어 숫자의 쌍을 부호까지 붙여서 순서대로 출력하도록 한다. 부호와 숫자 사이에는 공백이 없지만, 숫자와 숫자 사이는 공백 한 칸으로 구분해야 한다.
여러 가지 풀이가 존재하더라도 하나만 출력하면 된다. 그리고 이 제어 숫자로는 주문대로 유토피아를 순회하는 게 불가능하다면, 숫자 0 하나만을 출력하도록 한다.
입력 출력
4 +7 -1
7 5 6 1 3 2 4 8 -5 +2
4 1 2 1 -4 +3
+8 +6
입력 출력
4 +3 -2
2 5 4 1 7 8 6 3 -4 +5
4 2 2 1 -6 +1
+8 +7
답안 프로그램이 제한 시간 내에 입력 자료에 대한 맞는 답을 출력하면 만점을 받고, 그렇지 않으면 0점을 받는다. 이 문제는 25개의 입력 데이터로 채점을 받으며, 한 데이터 당 만점은 4점으로 최대 100점을 받게 된다. 한 데이터 당 시간 제한은 2초이며, 메모리 제한은 32MB이다.
당신은 손전화에 들어가는 응용 프로그램을 개발하고 있다. 이 기기의 화면은 흑백이다. 화면의 x 좌표는 왼쪽에서 시작하고, y 좌표는 위에서부터 시작한다. (그림 참조) 응용 프로그램에는 사용자들에게 친근감을 주게끔 여러 그림들이 들어간다. 그림들의 크기는 서로 다를 수 있다. 여러분은, 그림들을 있는 그대로 저장하는 게 아니라 전화기에 내장돼 있는 그래픽 라이브러리에 있는 루틴을 써서, 그림을 생성하려고 한다.
그림은 화면의 모든 픽셀이 흰색인 초기 상태에서부터 그려 나간다. 손전화에 내장돼 있는 유일한 그래픽 루틴은 XOR(L, R, T, B)이다. 이 명령은 화면에서 좌측 상단 (L, T) 위치에서부터 우측 하단 (R, B) 위치를 차지하는 직사각형 영역에 있는 점들의 색깔을 맞바꾼다. (하양은 검정으로, 검정은 하양으로)
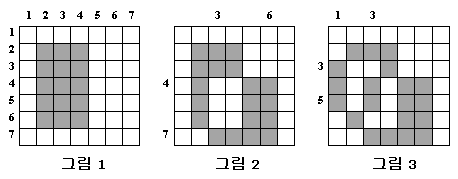
예를 들어, 그림 3과 같은 모양을 만든다고 생각해 보자. 초기 상태에서 XOR(2, 4, 2, 6)을 내리면 화면은 그림 1과 같이 된다. 다음에 XOR(3, 6, 4, 7)을 내리면 그림 1은 그림 2로 바뀐다. 마지막으로 XOR(1, 3, 3, 5)를 거기에다 내리면 그림 3이 완성된다.
흑백 비트맵 그림들이 있다. 당신의 과제는 초기 상태에서 XOR 명령을 가장 적게 내려서 그 그림들을 만드는 방법을 찾아낸 뒤, 그 그림을 만들기 위해 내린 XOR 명령 매개변수들을 제출하는 것이다. 이번 문제에서는 프로그램을 제출하는 게 아니라 출력 파일만 제출하면 된다.
xor1.in부터 xor10.in까지 그림 정보를 담고 있는 열 개의 텍스트 파일이 있을 것이다. 각 파일들은 다음과 같이 짜여 있다. 첫 줄에는 그림의 크기를 나타내는 정수 N (5≤N≤2000)이 있다. 이는 이 그림이 가로, 세로로 N칸인 정사각형임을 말한다. 그 뒤에는 N개의 숫자가 들어있는 수열이 N줄 나온다. 이들 숫자들은 위에서 아래로, 왼쪽에서 오른쪽으로 각 칸에 해당하는 픽셀 정보를 담고 있으며, 그 값은 0 아니면 1이다. 0은 흰색, 1은 검은색을 뜻한다.
각 입력 파일에 해당하는 출력 파일을 제출하면 된다. 각 파일의 크기는 1메가바이트보다 작아야 한다. 출력 파일의 첫 줄에는
#FILE xor I
라는 문구를 넣는다. 여기서 I는 이 출력 파일에 해당하는 입력 파일의 번호이다. 둘째 줄에는 이 그림을 그리기 위해 XOR 명령을 내린 횟수 K를 넣는다. 그리고 다음 K 개의 줄에는, XOR 명령에 전달한 매개변수들 L, R, T, B의 값 네 개를 명령을 내린 순서대로 출력한다.
xor0.in
7
0 0 0 0 0 0 0
0 1 1 1 0 0 0
1 0 0 1 0 0 0
1 0 1 0 1 1 0
1 0 1 0 1 1 0
0 1 0 0 1 1 0
0 0 1 1 1 1 0
xor0.out
#FILE xor 0
3
2 4 2 6
3 6 4 7
1 3 3 5
이 문제는 10개의 데이터로 채점을 받으며 답안 프로그램을 채점하는 게 아니라, 정해진 입력 파일 10개에 대해 여러분이 제출한 출력 답안만을 가지고 채점한다. 만약
그 답안의 점수는 0점이 된다. 그렇지 않으면 점수는
1+9*(모든 참가자들의 정답 중 XOR 명령을 가장 적게 내린 횟수)/(당신의 답이 명령을 내린 횟수)
가 된다.
한 출력 파일의 점수는 소숫점 둘째 자리에서 반올림된다. 또한 이 문제 전체의 총점은 가장 가까운 정수로 반올림된다. 예를 들어 당신이 XOR 명령을 121번 호출한 정답을 제출하였고 그것이 참가자들 중 가장 좋은 답안이라면 점수는 만점인 10점이 된다. 한편, 참가자들 중에 XOR 명령을 98번 내린 답이 있다면 당신의 점수는 1+9*98./121 (=8.289)이 되고, 이는 8.3점으로 반올림된다. 이 문제 전체의 만점은 100점이다.
한 기계가 있고, 그 기계가 차례대로 처리해야 할 작업들이 N개 있다. 각 작업들은 1부터 N까지 번호가 매겨져 있다. 기계 동작의 효율을 위해, 우리는 이 작업들을 하나 이상의 묶음으로 쪼개려고 한다. 예를 들어 작업이 여섯 개 있으면 {1, 2, 3}, {4}, {5, 6}이나 {1, 2}, {3, 4, 5}, {6}처럼 작업의 순서만 유지하면 어떤 식이든 가능하다.
이들의 처리는 0이라는 최초의 시각에 시작한다. 기계는 일들을 묶음 단위로 하나씩 처리하는데, 이들을 처리하는 순서 역시, 번호가 작은 작업들의 묶음부터 하는 걸로 정해져 있다. 즉 {1, 2} 묶음을 처리하지 않고 {6}부터 먼저 할 수는 없다. 묶음 안에 있는 작업들은 기계 안에서 순차적으로 처리되나, 어떤 묶음 안에 한 번 소속된 작업은 그 묶음에 있는 작업들 전체가 처리가 끝나기 전에는 결과가 나오지 못한다. 따라서 j째 작업의 완성 시간은 j가 속한 묶음 전체의 작업이 완성되는 시간과 같다.
첫 묶음의 작업을 시작하기 전에, 그리고 한 묶음에서 다른 묶음의 작업으로 넘어가기 전에는 기계를 시동시키기 위해 S라는 고정된 시간이 필요하다. 그리고 임의의 작업(번호가 i라면)을 하는데는 Fi라는 비용 계수와 Ti라는 시간이 필요하다. 어떤 묶음에 x, x+1, ..., x+k라는 작업이 들어가 있고 이 묶음의 처리를 t라는 시각에 시작시켰다면 그 묶음 안에 있는 모든 작업들이 끝나는 시각은 t + S + (Tx + Tx+1 + ... + Tx+k)가 된다. 앞에서 말했듯이, 작업의 결과는 작업 하나가 끝나는 대로 차곡차곡 나오는 게 아니라, 묶음에 있는 모든 작업들이 끝나야 그것들의 결과가 한꺼번에 출력되기 때문이다.
위의 요소(묶음 안의 다른 일들 때문에 걸리는 지연 시간, 시동 시간)를 고려하여 i째 작업이 끝나는 데 실제로 걸리는 시각이 Oi라면, 그 작업의 비용은 Oi×Fi가 된다. Oi는 시간이 아니라 시각이다. 따라서 Ti가 같은 작업이라도 앞의 묶음 때문에 늦게 시작한 작업은 비용이 커진다. 예를 들어, 해야 할 작업이 다섯 개 있어 (T1, T2, T3, T4, T5) = (1, 3, 4, 2, 1)이며, (F1, F2, F3, F4, F5) = (3, 2, 3, 3, 4)이라고 하자. 그리고 기계의 시동 시간 S는 1이라고 하자. 만약 이 일들을 {1, 2}, {3}, {4, 5}라는 세 묶음으로 분할하면 완료 시각인 (O1, O2, O3, O4, O5)는 차례대로 (5, 5, 10, 14, 14)가 된다. 첫째 묶음의 완료 시각은 S+T1+T2=1+2+2=5이고, 둘째 묶음의 경우는 S+T3=5에다 앞의 5를 더한 10, 그리고 마지막 묶음의 처리 완료 시각은 S+T4+T5=4에다 10을 더한 14인 것이다. 그리고 이 작업들의 비용은 각 수에다 Fn을 곱한 (15, 10, 30, 42, 56)이 된다. 따라서 총 작업 분할 비용은 이 비용들의 합인 153이 된다.
총 비용을 줄이기 위해서는 지연 시간이 적도록 작업들을 효율적으로 분할해야 한다. 하지만 묶음이 바뀔 때마다 드는 기계의 시동 시간도 고려해야 한다. 기계의 시동 시간과, 각 일들의 처리 시간과 비용 계수를 입력받아, 있을 수 있는 가장 적은 분할 비용을 계산하는 프로그램을 작성하시오.
표준 입력 스트림에서 데이터를 읽어들인다. 첫째 줄에는 작업의 총 개수 N이 있다. (1≤N≤10000) 둘째줄에는 묶음이 바뀔 때의 기계 시동 시간인 정수 S가 있다. (0≤S≤50) 그리고 다음 N줄에는 1, 2, ..., N째 작업에 대해 그 작업의 처리 시간인 Ti와(1≤Ti≤100) 비용 계수인 Fi (1≤Fi≤100)이 순서대로 들어있다.
표준 출력 스트림으로 답을 출력한다. 작업 분할 비용의 최소값을 나타내는 자연수 하나를 한 줄에다 출력한다.
입력 출력 (1번 예제)
2 45000
50
100 100
100 100
입력 출력 (2번 예제)
5 153
1
1 3
3 2
4 3
2 3
1 4
2번 예제는 문제에서 나왔던 데이터이다.
일러두기: 채점 과정에서 작업 분할 비용이 231-1을 넘는 일은 발생하지 않는다.
답안 프로그램이 제한 시간 내에 입력 자료에 대한 맞는 답을 출력하면 만점을 받고, 그렇지 않으면 0점을 받는다. 이 문제는 20개의 입력 데이터로 채점을 받으며, 한 데이터 당 만점은 5점으로 최대 100점을 받게 된다. 한 데이터 당 시간 제한은 0.1초이며, 메모리 제한은 32MB이다.
용인 시는 버스 정류장이 N개 있는 버스 노선을 짜려고 한다. 각 버스 정류장은 거리의 모퉁이에 있다. 용인 시는 현대적으로 설계된 도시이기 때문에 지리 구조가 정사각형 격자 모양으로 짜여 있다. 우리는 이 버스 정류장들 가운데 두 곳을, 중심지로서 H1, H2라는 이름으로 선택하려고 한다. 중심지를 선택하고 나면, 두 중심지 사이에는 버스가 가는 길이 생기며, 중심지를 제외한 나머지 N-2개의 버스 정류장들은 H1 아니면 H2 중 한 곳(두 중심지 모두와 연결되는 것은 아님.)과 직통하게 될 것이다. 이렇게 버스 노선이 결정된다.
이 문제에서 임의의 두 지점 사이의 거리는, 두 곳을 수평 수직 방향으로만 통행하는 가장 가까운 거리이다. 다시 말해, 위치를 (x, y) 좌표로 표현했을 때, 두 지점 (x1, y1)과 (x2, y2)의 거리는 |x1-x2|+|y1-y2|로 정의된다는 뜻이다. 한편, 버스 정류장 A와 B가 같은 중심지 H1과 연결돼 있으면 두 정류장 사이의 거리는 A와 H1 사이의 거리와 H1과 B 사이의 거리의 합이 된다. 그리고 A와 B가 각각 다른 중심지인 H1, H2와 연결돼 있으면 두 정류장 사이의 거리는 A와 H1, H1과 H2, H2와 B 사이의 거리들의 합이 된다.
용인 시의 도시 계획부는, 모든 시민이 도시의 모든 구역에 최대한 빨리 도착할 수 있게 하길 원한다. 따라서 도시 계획자들은 버스 정거장들 중, 서로 가장 멀리 떨어져 있는 두 곳 사이의 거리를 최소화할 수 있게끔 중심지 두 곳을 고르려고 한다. 이 거리를 최소화하게 중심지를 고른 뒤, 서로 거리가 가장 먼 두 정류장 사이의 거리를 계산하는 프로그램을 작성하시오.
표준 입력 스트림에서 데이터를 읽어들인다. 첫째 줄에는 버스 정류장의 개수인 정수 N(2≤N≤500)이 있다. 그리고 다음 N 개의 줄에는 버스 정류장의 x, y좌표가 있다. (가로 먼저, 다음 세로) 각 좌표들은 5000과 같거나 작은 자연수이다. 정류장들은 모두 서로 다른 위치에 있으며, 겹치는 경우가 없다.
표준 출력 스트림으로 답을 출력한다. 거리가 가장 먼 두 정류장 사이의 거리의 최소값을 나타내는 자연수 하나를 한 줄에다 출력한다.
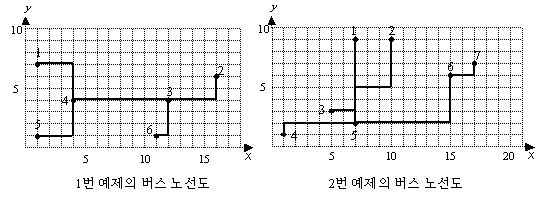
예제 파일을 바탕으로 버스 노선도를 구성한 그림이 오른쪽에 있다. 1번 예제에서 3번과 4번 정류장을 중심지로 선택하면, 2번과 1번 정류장 사이, 그리고 2번과 5번 정류장 사이가 거리가 가장 멀게 되고 이 때 거리는 20이다. 중심지를 어떤 것을 골라도 가장 먼 정거장 사이의 거리를 20보다 짧게 할 수는 없기 때문에 20이 이 답안의 정답이다.
한편 2번 예제의 경우, 5번과 6번 정류장을 중심지로 선택하면, 가장 먼 정류장의 쌍은 2번과 7번 정류장이 된다. 그 거리는 25이다. 중심지를 어떤 것을 골라도 가장 먼 정거장 사이의 거리를 25보다 짧게 할 수는 없기 때문에 25가 정답이다.
 입력
출력 (1번 예제)
입력
출력 (1번 예제)
6 20
1 7
16 6
12 4
4 4
1 1
11 1
입력 출력 (2번 예제)
7 25
7 9
10 9
5 3
1 1
7 2
15 6
17 7
답안 프로그램이 제한 시간 내에 입력 자료에 대한 맞는 답을 출력하면 만점을 받고, 그렇지 않으면 0점을 받는다. 이 문제는 20개의 입력 데이터로 채점을 받으며, 한 데이터 당 만점은 5점으로 최대 100점을 받게 된다. 한 데이터 당 시간 제한은 4초이며, 메모리 제한은 32MB이다.
N×N 크기의 격자 평면에 가로 막대와 세로 막대가 하나씩 있다. 이 문제에서 막대란, 격자로 된 정사각형 평면에서 가로나 세로 방향으로 두 칸 이상을 차지하는 선을 말한다. 아래 그림에서 두 막대는 X로 나타나 있다. 두 막대의 길이는 서로 같을 수도 있고 다를 수도 있다. 또한 같은 칸을 공유할 수도 있다. 만약 아래 그림의 (4, 4) 좌표처럼 가로 막대가 놓인 점이라고도 볼 수 있고 세로 막대가 놓인 점이라고도 볼 수 있는 점이 있다면, 그 점은 언제나 두 막대가 모두 걸친 점이라고 약속하기로 한다. 따라서 세로선의 위쪽 끝 좌표는 (5, 4)가 아니라 (4, 4)가 된다. (세로 좌표 다음에 가로 좌표가 옴)
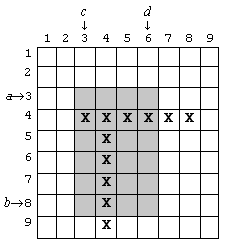
처음에 우리는 두 막대가 길이가 몇이고 평면 어디에 놓여 있는지 알지 못한다. 여러분의 과제는 이들의 위치를 구하는 프로그램을 작성하는 것이다. 평면의 각 칸의 좌표는 (줄 번호/세로, 칸 번호/가로)로 나타내며, 평면 좌측 상단의 좌표는 (1, 1)이다. 그리고 막대는 두 좌표를 써서 <(r1, c1), (r2, c2)>로 표현한다. 따라서 위 그림에서 가로 막대는 <(4, 3), (4, 8)>이 되고, 세로 막대는 <(4, 4), (9, 4)>가 된다.
이번 문제에서는 입력을 받고, 해답을 구하고, 출력을 하는 데 라이브러리를 쓴다. 각 테스트 케이스마다, 먼저 gridsize 함수로 정사각형 격자 평면의 한 변의 길이를 파악한다. 다음, 막대를 찾는데는 rect(a, b c, d) 함수만을 쓸 수 있다. 이 함수는 [a, b]×[c, d] 직사각형 영역에 속한 격자들(a≤b이고, c≤d이다. 위 그림에서는 어둡게 칠해진 영역을 가리킨다. 좌표가 들어가는 순서를 주의깊게 살펴보기 바란다.)을 살펴서 여기에 막대기가 놓인 곳(X로 표시된 칸)이 한 군데라도 있으면 1을 되돌리고, 그렇지 않으면 0을 되돌린다. 따라서 위의 예에서 rect(3, 8, 3, 6)의 함수값은 1이다. 당신은 제한된 횟수만큼만 rect 함수를 호출하여 두 막대의 정확한 크기와 위치를 구하는 프로그램을 작성해야 한다.
출력은 report(r1, c1, r2, c2, p1, q1, p2, q2)로 하면 된다. 이는, 가로 막대의 위치는 <(r1, c1), (r2, c2)>이며, 세로 막대의 위치는 <(p1, q1), (p2, q2)>임을 뜻한다. report 함수를 호출하면 답안 프로그램의 실행은 끝난다. (r1, c1)은 가로 막대의 왼쪽 끝의 위치이며, (p1, q1)은 세로 막대의 위쪽 끝의 위치이다. 따라서 r1=r2, q1=q2이며, c1≤c2, p1≤p2임이 성립해야 한다. 만약 답안 프로그램이 report 함수에 제출한 매개변수들이 이 조건을 만족하지 않으면 표준 출력 스트림에 에러 메시지가 나올 것이다.
이번 문제에서 사용하는 라이브러리의 스펙은 다음과 같다.
프리파스칼 용 (prectlib.ppu, prectlib.o)
function gridsize: LongInt;
function rect(a,b,c,d : LongInt) : LongInt;
procedure report(r1, c1, r2, c2, p1, q1, p2, q2 : LongInt);
답안 프로그램인 rods.pas를 컴파일하려면 소스 코드에 다음 들임문을 넣고,
uses prectlib;
다음과 같이 컴파일한다.
fpc -So -O2 -XS rods.pas
prodstool.pas 프로그램에 이 라이브러리를 쓰는 예제가 나와 있다.
GNU C/C++ 용 (crectlib.h, crectlib.o)
int gridsize();
int rect(int a, int b, int c, int d);
void report(int r1, int c1, int r2, int c2, int p1, int q1, int p2, int q2);
답안 프로그램인 rods.c를 컴파일하려면 소스 코드에 다음 들임문을 넣고,
#include "crectlib.h"
다음과 같이 컴파일한다.
gcc -O2 -static rods.c crectlib.o -lm
g++ -O2 -static rods.cpp crectlib.o -lm
prodstool.c 프로그램에 이 라이브러리를 쓰는 예제가 나와 있다.
RHIDE의 C/C++ 환경이라면
Option->Linker 설정에 crectlib.o를 넣었는 지 확인하기 바란다.
실제로 채점하지 않는 환경에서 라이브러리를 수동으로 조작하기 위해서는 rods.in 파일을 생성해야 한다. 여기에는 세 줄을 넣는다. 첫째 줄에는 격자의 크기인 N을 넣는다. 둘째 줄에는 가로 막대의 좌표인 r1, c1, r2, c2를 넣는다. r1, c1은 가로 막대의 왼쪽 끝 좌표이다. 그리고 셋째줄에는 세로 막대의 좌표인 p1, q1, p2, q2를 넣는다. 여기서 p1, q1은 세로 막대의 위쪽 끝 좌표이다.
그 뒤, 답안 프로그램이 report 함수를 호출하여 실행이 끝나면, rods.out 파일이 생겨난다. 이 파일에는 가장 먼저 답안 프로그램이 rect 함수를 호출한 횟수가 들어있으며, 답안 프로그램이 report 함수로 제출한 가로, 세로 막대의 좌표가 그 뒤에 나온다. 만약 라이브러리 함수를 호출하는 과정에서 제한사항을 어긴 경우가 있었다면 rods.out에는 그에 따른 에러 메시지도 들어있게 된다.
답안 프로그램과 라이브러리가 rect 함수로 의사 소통을 한 모든 기록은 rods.log 파일에 기록된다. 이 파일은 "k : rect(a, b, c, d) = ans"와 같은 형태의 줄들의 나열을 수록하고 있는데, 답안 프로그램이 rect 함수를 k째로 호출했을 때, a, b, c, d와 같은 인자를 넘겨주어, ans와 같은 되돌림값을 얻었음을 보여준다.
rods.in
9
4 3 4 8
4 4 9 4
rods.out
20
4 3 4 8
4 4 9 4
답안 프로그램이 제한 사항을 어기거나 (rect 함수를 400번 이상 호출하는 등) 프로그램이 답을 틀리게 구하면 그 테스트 케이스의 점수는 0점이 된다.
그렇지 않으면 점수는 답안 프로그램이 rect 함수를 호출한 횟수에 따라 달리 매겨진다. 이 함수를 100번 이하로 호출하여 답을 맞게 구했으면 만점인 5점을 얻고, 101~200번 호출했으면 3점을 얻는다. 그리고 201~400번 호출했으면 1점을 얻는다.
이 문제는 20개의 입력 데이터로 채점을 받으며, 각 데이터 당 만점이 5점이므로 최대 100점을 받게 된다. 한 데이터당 시간 제한은 1초이며, 메모리 제한은 32MB이다.