제 15회

제 15회는 2003년 8월 16일부터 23일까지 미국 위스콘신 주 케노사(Kenosha)에서 열렸다. 이번 대회에서 쓰인 하드웨어 환경은 램 256MB, 2.2GHz인 펜티엄 4였으며, (작년 우리나라 대회 때에 비해 500MHz가 더 빨라짐) 소프트웨어 환경은 별다른 변화가 없었다.

목축업이 발달한 도시답게 농장을 배경으로 하는 문제가 눈에 띈다. 1번은 인터렉티브 문제이며, 3번은 답안 프로그램 대신 테스트 케이스에 대한 답만 제출하면 되는 문제이다. 4번은 99년 3번을 떠올리게 하는 문제이며, 6번은 오랜만에 나온 기하 문제여서 느낌이 새롭다.

우리나라는 이번 대회에서 금메달 둘, 은메달 둘을 획득해 공동 1위를 차지했다. 특히 우리나라 선수 중 한 명이 600점 만점에 455.4점으로 종합 1위의 영예도 누렸다. (2등과의 점수 차이는 약 29점) 한편, 동메달 입상자의 최저 점수는 173.1점이었다.

원문이 있는 곳: http://www.ioi2003.org/tasks.htm

1. 발자국 경로 고르기 (대화형)

2. 코드 비교

3. 내림차순 출력 (제출형)

4. 알아맞히기 (대화형)

5. 로봇 구출

6. 울타리

1. 발자국 경로 고르기 (대화형)

농부인 존이 거느리고 있는 소들은 N개의 들판(1부터 N까지 번호가 매겨짐. 1<=N<=200)을 자유롭게 드나들고 싶어한다. 하지만 들판 사이엔 숲이 있어서 그렇게 하기 힘들다. 그래서 소들은 두 들판 사이에 산짐승들이 이미 먼저 낸 길을, 발자국을 보고 가려고 한다. 길에 방향 구분은 없기 때문에, 이쪽에서 저쪽으로 가는 길이 있으면 저쪽에서 돌아오는 것도 가능하다.

매 주(week)마다 산짐승들이 임의의 들판에서 다른 들판까지 낸 발자국 경로가 하나씩 발견된다. 그러면 소들은 자신이 원하는 발자국 경로만 골라 그것이 지워지지 않게 보존한다. 산짐승들은 직선 거리 같은 건 알지 못하기 때문에 출발지와 목적지가 같더라도 여러 경로를 만들어 낼 수 있으며, 소들은 거리가 더 짧은 경로가 생겨 있으면 예전 것을 지우고 새로운 것을 택할 수 있다. 우리의 목적은, N개의 들판에서 어느 곳에서도 모든 곳으로 갈 수 있는 발자국 경로 노선을 구축하되, 새로운 발자국 경로가 매주 발견될 때마다 짧은 것을 골라서 경로들의 합이 최소가 되게 하는 것이다.

주 첫날마다 소들은 새로 발견한 발자국 경로의 위치, 방향과 그 거리를 보고한다. 당신의 프로그램은 그때 그때 이들을 종합하고 최적의 노선을 업데이트하여, 모든 들판을 서로 연결하면서 거리의 합이 최소가 되는 발자국 경로들의 거리의 합을 출력해야 한다. (그런 경로가 있는 경우에만)

입력 (표준 입력)

첫 줄에는 들판의 개수 N과 W의 값이 들어온다. 두 수는 공백으로 구분돼 있으며, W는 발자국이 들어오는 총 기간, 즉 횟수이다. (1<=W<=6000)

이제 매 주에 하나씩 들어오는 발자국 경로에 대한 정보가 한 줄에 들어온다. 이것은 세 정수의 형태인데, 각각 이 경로가 연결하는 두 들판의 번호와, 이 경로의 거리이다. (1...10000) 시작점과 끝점이 같은 경로를 만드는 산짐승은 없다.

출력 (표준 출력)

산짐승이 발견해 낸 새로운 발자국 경로에 대한 정보를 입수한 즉시(=다음 입력을 읽어들이기 전에), 모든 들판을 서로 연결하면서 거리의 합이 최소가 되는 발자국 경로들의 거리의 합을 정수로 한 줄에 출력해야 한다. 아직 한 들판에서라도 단 한 군데라도 다른 들판으로 가는 길이 생겨 있지 않다면 -1을 출력한다. 하지만 경로들이 꼭 완전 그래프를 이루고 있어야 할 필요는 없다. 또다른 들판을 거쳐서 목적지로 가도 되기 때문이다.

마지막 입력에 대한 출력을 한 뒤, 프로그램 실행을 끝내면 된다.

비고

• 실행 제한: 실행 시간 1초, 메모리 제한 64MB
• 채점: 각 테스트 케이스마다 정답을 출력하면 만점을 받는다. 한 질문에라도 틀린 대답을 하면 그 케이스 전체 점수의 점수는 0점이 되며, 부분 점수는 없다.

2. 코드 비교

라신 비즈니스 네트워크(이하 라비네) 사는, 휴리스틱 알고리즘 언어(이하 휴알) 사를 상대로 소송을 제기했다. 자신의 라비네 유닉스(TM)의 소스 코드를 휴알 사가 자신의 오픈 소스 운영체제인 휴알닉스에 무단 도용했다는 것이다.

라비네와 휴알은 모두, "변수A = 변수B + 변수C" 꼴의 구문이 한 줄에 하나씩 오는 형태의 프로그래밍 언어를 사용한다. 등호와 +의 앞뒤에는 모두 공백이 한 칸 있으며, 변수A 앞에는 공백이 없다. 한 줄에 같은 변수 이름이 여러 번 등장할 수도 있다. 변수는 로마자 알파벳 대문자가 최소 한 자, 최대 여덟 자 모인 형태이다.

라비네 측은 휴알이 자사의 소스 코드의 한 부분을 뭉텅(띄엄띄엄이 아니라 연속적으로) 베껴서 그들의 코드의 일부로 삽입한 뒤, 다음과 같은 방법으로 변형만 했을 것이라고 주장한다.

• 베꼈다는 티를 내지 않기 위해 한 변수 이름을 다른 것으로 모두 바꾼다. 물론, 서로 다른 이름이던 변수들을 같은 이름으로 통합하지는 않는다.
• 덧셈은 교환 법칙이 성립하기 때문에, 베낀 코드 중에서 어떤 줄은 우항의 변수 배열 순서를 바꾼다. (예를 들어 A = B + C를 A = C + B로.)
• 하지만 코드의 실행 순서 자체를 바꾸지는 않는다.

라비네 사와 휴알 사의 소스 코드를 보고, 휴알 사가 위의 조건을 만족하면서 라비네 사 코드를 최대 얼마나 베꼈을 것인지 추정하는 프로그램을 작성하시오. 휴알 사의 코드 중 어느 부분(전부일 수도 있음)이 라비네 코드의 어느 부분을 베낀 것인지는 알 수 없으므로, 프로그램이 판단해야 한다.

입력 (code.in)

첫 줄에는 R과 H가 있다. (공백으로 구분, 1<=R<=1000, 1<=H<=1000) 각각 라비네 사와 휴알 사의 소스 코드의 길이를 의미한다. 그 뒤 R 줄에는 라비네 사의 프로그램이 있으며, 다음 H 줄에는 휴알 사의 프로그램이 있다.

4 3
RA = RB + RC
RC = D + RE
RF = RF + RJ
RE = RF + RF
HD = HE + HF
HM = HN +D
HN = HA + HB

출력 (code.out)

휴알 사가 라비네 사의 코드를 베껴서 변형했을 것이라 추정되는 가장 긴 연속적인 부분의 줄 수를 출력하면 된다.

2

예제 입력에서 라비네 프로그램의 1-2째 줄이 휴알 프로그램의 2-3째 줄과 일치한다. 원본 프로그램에서 RA가 HM으로, RB가 D로, RC가 HN으로, D가 HA로, RE가 HB로 바뀐 것이다. 하지만 세 줄이 연달아 일치하는 부분은 없다.

비고

• 실행 제한: 실행 시간 2초, 메모리 제한 64MB
• 채점: 각 테스트 케이스마다 정답을 출력하면 만점을 받는다. 부분 점수는 없다.

3. 내림차순 출력 (제출형)

1부터 9까지 레지스터가 아홉 개 있고, 두 가지 명령을 지원하는 컴퓨터가 있다. 각 레지스터에는 0이상 1000 이하 범위의 정수가 들어갈 수 있으며, 지원하는 명령은 다음과 같다.

• S i j: i번 레지스터에 있는 값에 1을 더한 값을 레지스터 j에 저장한다.
• P i: i번 레지스터에 있는 값을 출력한다.

이 컴퓨터에서 돌아가는 프로그램은 아홉 레지스터에 들어갈 초기값과, 이들을 조작하는 S, P 명령의 나열로 되어 있다. N이라는 정수가 있을 때(0<=N<=255), N부터 시작하여 N-1, N-2, ..., 0을 내림차순으로 출력하는 프로그램을 작성하여 제출하시오.

N=2일 때 이 일을 하는 프로그램 중 하나는 다음과 같다.

각 테스트 케이스 파일은 1부터 16까지 번호가 매겨져 있으며 컨테스트 서버를 통해 내용을 볼 수 있다.

입력

두 줄에 케이스를 식별하는 번호 K와 이 경우 풀어야 하는 N 값이 각각 들어있다.

1
2

출력

제출하는 출력의 첫 줄은 "FILE reverse K" (K는 해당하는 테스트 케이스 번호)로 시작해야 한다. 둘째 줄에는 아홉 개의 레지스터의 초기값을 공백으로 구분하여 1번 레지스터에서부터 9번 레지스터의 것까지 순서대로 출력한다. 그리고 다음 줄부터는 내리고자 하는 명령을 한 줄에 하나씩 출력하여, 맨 마지막에는 0을 출력하는 명령이 있어야 한다. 위의 입력에 대한 바른 출력 예를 두 가지 들면 다음과 같다.

채점

각 테스트 케이스에 대한 채점은 제출한 프로그램의 정확성과 효율성을 기준으로 한다.

• 정확성 (20%): 프로그램이 출력해 내는 숫자의 개수와 내용이 정확히 일치해야 한다. (N부터 0까지 내림차순으로 N+1개의 숫자) 또한 P 명령을 한 번 내리기 전에 S 명령은 연속해서 131회 이하로만 내려야 하며, 연산 과정에서 오버플로우를 일으켜서는 안 된다. (1000 이내의 범위)
• 효율성 (80%): 한 테스트 케이스의 출력에는 S 명령을 연속해서 가장 많이 내리는 부분이 있다. 이것이 테스트 케이스를 평가하는 기준이며, 그 최대치가 작을수록 효율적인 프로그램이다. 효율성 채점은 참가자들 중 그 값이 가장 작은 참가자의 값과 당신의 값과 차이를 비교해서 행해진다.

4. 알아맞히기

존의 농장에는 N마리의 소가 있으며, 이들은 1부터 N까지 번호가 매겨져 있다. (1<=N<=50) 소들은 서로 비슷하게 생겼기 때문에 존은 이 소가 어느 소인지 알아야 이들을 각 소에 해당하는 맞는 외양간에 넣을 수 있다.

이 소들을 구분하는 특성이 P개 존재하며, (1<=P<=8) 각 특성은 세 가지 중에서 한 값을 갖는다. 예를 들어 소의 귀에 달린 꼬리표의 색깔도 특성 중 하나가 될 수 있고, 이것은 노랑, 초록, 빨강의 세 가지 중 하나인 것이다. 이 문제에서는 간결성을 위해 특성의 값은 X, Y, Z라는 형태로 통일해서 나타나기로 한다. 존이 거느리고 있는 각 소들은 특성 중 적어도 하나는 서로 다르다.

각 소들의 모든 특성을 입력받은 뒤, 농부에게서 자신이 원하는 소의 특성을 질문하여 대답을 받아서, 농부가 원하는 소 한 마리를 알아맞히는 프로그램을 작성하시오. 프로그램이 할 수 있는 질문의 형태는 "원하는 소의 아무개 특성이 아무개 중에 있는가?"뿐이며, 질문을 100번 이내로 가능한 한 적게 해서 소를 찾아야 한다.

입력 (guess.in)

첫 줄에는 N과 P의 값이 각각 들어있다. 그리고 다음 N 줄에는 1번 소에서 N번 소까지 각 소의 1번부터 P번 특성의 값이 차례로 들어있다.

4 2
X Z
X Y
Y X
Y Y

인터렉티브 입출력 (표준 입출력)

질문은 표준 출력으로 하고, 답변은 표준 입력에서 읽어들인다.

질문은 "Q 특성_번호 하나_이상의_값"의 형태로 한다. 예를 들어 "Q 1 Z Y"는 "원하는 소의 1번 특성의 값은 Z 혹은 Y인가?"란 뜻이다. 특성 번호는 1부터 P 사이에 있어야 하며, 속성값은 X, Y, Z 중 하나여야 한다. 한 질문에 같은 속성값이 중복해서 등장해서는 안 된다.

이렇게 질문을 한 뒤에는 숫자 하나를 한 줄에서 읽는다. 1은 그 질문의 '예'에 해당하는 대답이며, 0은 '아니오'라는 대답이다. 질문과 답변을 충분히 주고받은 뒤에는 "C 찾은_소의_번호"를 출력하고 프로그램을 끝낸다.

다음은 위의 입력 파일에 대한 인터렉티브 입출력의 예이다.

비고

• 실행 제한: 실행 시간 1초, 메모리 제한 64MB

채점

• 정확성 (30%): 질문을 적절히 하여 이들 답변을 만족하는 소가 하나밖에 남지 않았고(즉, 질문 과정도 보기 때문에 답만 맞으면 안 됨), 그 소를 올바르게 맞혔다면 정확성에서 만점을 받는다. 다만, 질문을 100번을 초과하여 하면 그 테스트 케이스의 점수는 0점이 된다.
• 질문 횟수 (70%): 나머지 점수는 맞는 소를 찾기 위해 한 질문의 횟수에 따라 결정된다. 테스트 케이스들은 우연적인 요소를 최소화하도록 설계돼 있다. (즉, 특정 번호나 특정 순서대로 소의 특성을 질문하면 문제 해결의 실마리를 더 빨리 찾을 수 있는 것) 최소 질문 횟수에 얼마나 근접하느냐에 따라 부분 점수를 준다.

5. 로봇 구출

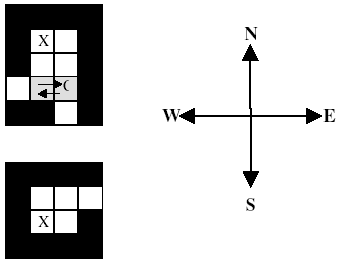
당신은 서로 다른 미로 안에 갇혀 있는 두 로봇을 갖고 있다. 미로에서 (1, 1)은 좌측 상단 위치이자 북서쪽 끝을 나타낸다. 각 미로(i번 미로. i=1 or 2)에는 Gi (0<=Gi<=10)명의 악당이 수평 또는 수직 방향으로 순찰하면서 로봇을 붙잡으려고 한다. 이번 문제의 목표는 두 로봇을 잘 조종하여, 악당에게 붙잡히지 않고 무사히 미로 밖으로 구출하는 것이다.

로봇에게 내리는 명령은 동서남북 중 한 곳으로 한 칸씩 움직이는 것인데, 매 단위 시각마다 하나씩 내릴 수 있다. 그런데 두 로봇을 같이 이동시킬 수만 있고, 한 로봇은 가만 있게 하거나 서로 다른 방향으로 가게 하지는 못한다. 다만, 두 로봇 중에 명령을 내린 방향에 벽이 있어서 움직이지 못하는 게 있다면, 이동할 수 있는 것만 움직인다. 미로 영역의 좌표를 벗어난 로봇은 목적을 달성했기 때문에, 그 이후로는 명령에 응하지 않는다.

악당의 순찰 경로는 벽을 관통하지도 않으며 미로를 벗어나지도 않는다. 여러 악당의 경로가 겹칠 수는 있으나, 한 순간에 둘 이상의 악당이 한 위치에 있거나, 서로 마주보고 이동하여 위치를 교환하는 경우는 없다. 또한, 악당이 처음부터 로봇과 같은 위치에 있지도 않는다. 로봇과 악당이 같은 위치에 있거나, 한 시점에 마주보고 움직여서 위치를 교환하게 되면 그 로봇은 악당에게 붙잡힌다.

두 미로(크기는 모두 20x20 이하)와 각 미로에 하나씩 배치된 두 로봇의 초기 위치, 그리고 악당의 초기 위치와 그들의 순찰 위치를 입력받아서, 두 로봇을 악당에게 붙잡히지 않고 잘 탈출시키는 명령을 생성하는 프로그램을 작성하시오. 명령의 효율성은 두 로봇이 모두 탈출한 시각만으로 평가되기 때문에, 두 로봇이 서로 다른 시각에 탈출한다면 먼저 미로를 빠져나간 로봇은 아무리 일찍 나갔다 하더라도 소용없다. 마지막 로봇이 탈출하는 데 걸리는 시간을 줄여야 한다.

입력 (robots.in)

입력 파일은 1번 미로에 대한 사항과 2번 미로에 대한 사항으로 나뉘어 있으며, 각 미로를 기술하는 형식은 서로 같다.

• 첫 줄에는 1번 미로의 세로 크기와 가로 크기를 나타내는 R1, C1이 있다. (공백으로 구분)
• 그리고 다음 R1개의 줄에는 미로 형태를 나타내는 C1개의 문자열이 붙어 있다. X는 로봇의 초기 위치를 나타내고, .는 열린 공간을, #은 벽을 뜻한다. 한 미로에는 X가 하나만 존재한다.
• 그 다음 줄에는 1번 미로에 있는 악당의 수를 나타내는 G1의 값이 있다. (0<=G1<=10)
• 다음 G1개의 줄에는 각 악당의 초기 위치와 이들이 순찰하는 방향을 기술하는 세 정수와 문자 하나가 공백으로 구분되어 들어있다. 첫 두 숫자는 악당이 처음에 있는 곳의 줄과 칸 위치이다(세로 다음에 가로). 다음에 오는 숫자는 이 악당이 움직이는 크기(칸 수)이다. 마지막으로 오는 문자는 그 방향이며, 그 값은 'N', 'S', 'E', 'W' 중 하나이다. (각각 북, 남, 동, 서쪽)

2번 미로에 대한 정보도 이와 완전히 똑같은 형식으로 바로 뒤이어 들어온다. 하지만 미로의 생김새, 악당 수, 심지어 미로의 크기까지 1번과는 다를 수 있다.

5 4
####
#X.#
#..#
...#
##.#
1
4 3 2 W
4 4
####
#...
#X.#
####
0

출력 (robots.out)

두 로봇을 악당과 마주치지 않고 같이 미로를 탈출시킬 수 있는 명령 나열을 계산해 낸 뒤, 그 횟수 K를 첫 줄에 출력한다. (K<=10000) 테스트 케이스는 언제나 10000회 이하의 명령을 내리고도 풀 수 있게 출제된다. 그렇지 않으면 로봇을 탈출시키는 것이 불가능한 경우이다. 만약 해가 존재한다면 다음 K개의 줄에는 그 명령들을 순서대로 출력한다. 한 줄에 N, S, E, W 한 문자씩 출력하면 된다. 해가 없는 테스트 케이스라면 첫 줄에 -1만 출력하도록 한다.

명령을 모두 내리고 나면 두 로봇이 모두 미로를 빠져나간 상태여야 하며, 특히 마지막 명령은 최소한 한 로봇을 미로를 탈출시키는 동작이어야 한다. 최소한의 명령 횟수로 로봇을 탈출시키는 방법이 여러 개 존재하더라도 아무 거나 하나만 찾아내면 된다.

8
E
N
E
S
S
S
E
S

비고

• 실행 제한: 실행 시간 2초, 메모리 제한 64MB

채점

두 로봇을 모두 무사히 구출하는 방법이 없는 테스트 케이스에는 부분 점수가 존재하지 않는다. 하지만 해가 존재하는 경우에는 다음과 같이 부분 점수가 인정된다.

• 정확성 (20%): 출력 형식을 잘 지키고, 10000회 이하의 명령으로 두 로봇을 무사히 탈출시킬 수 있는(마지막 명령이 정확히 한 로봇 이상을 탈출시키는 동작임) 동작을 생성하면 정확성에서 합격이다.
• 최적해 여부 (80%): 정확성을 만족하면서, 명령을 내린 횟수가 로봇을 탈출시킬 수 있는 최소한의 횟수라면, 최적해이다. 정확하지만 최소한의 횟수를 구하지 못한 답안은 최적해에 대한 점수를 받지 못한다.

6. 울타리

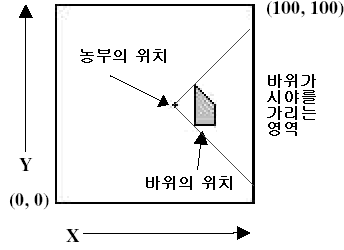
농부인 던은 자신의 밭을 감싸는 울타리를 관리하고 있다. 밭은 가로 세로 N미터인 정사각형 평지이다. (2<=N<=500000) 밭 경계의 한쪽 끝 좌표는 (0, 0)이며, 맞은편 끝 좌표는 (N, N)이다. 또한 경계는 x, y 축에 평행하다.

울타리를 나타내는 말뚝은 일단 밭의 네 모서리에 박혀 있고, 그 사이 네 변 구간에도 1미터 간격으로 박혀 있다. 따라서 말뚝은 총 4N개가 있다. 이 문제에서 말뚝은 땅 위로 솟아 있는 홀쭉한 선분이며 반지름, 즉 굵기가 없다고 가정한다. 던은 밭 안 어느 위치에 서서 사방을 돌아볼 때, 거기서 밭의 끝 경계에 있는 말뚝을 몇 개까지 볼 수 있나 알고 싶어한다.

그의 밭 안에는 R (1<=R<=30000)개의 커다란 바위가 있어서 그의 시야를 일부 가린다. 바위는 밑면과 윗면이 같은 볼록다각형으로 구성된 기둥이며, 높이가 충분히 높기 때문에 던은 바위 너머로 있는 말뚝을 볼 수 없다. 바위들은 영역이 서로 겹치지 않으며, 꼭지점이나 선분이 접하지도 않는다. 한 바위가 다른 바위 안이나 위에 있지도 않다.

던이 가진 밭(울타리)의 크기, 던이 밭 안에 있는 위치, 그리고 각 바위들에 대한 정보가 들어왔을 때, 그가 그 위치에서 고개만 돌려서 볼 수 있는 울타리 말뚝의 총 개수를 계산하는 프로그램을 작성하시오. 바위를 구성하는 임의의 한 정점과 농부와 일직선을 이루는 말뚝은 농부에게 보이지 않는다.

입력 (boundary.in)

첫 줄에는 N과 R의 값이 순서대로 들어있다. 다음 줄에는 던의 x, y 위치가 순서대로 들어있다. 그리고 다음 줄에는 R개의 바위에 대한 정보가 순서대로 들어온다.

바위에 대한 정보는 다각형을 기술하는 것과 같으므로, 가장 먼저 이 바위의 꼭지점 개수를 나타내는 p가 있다. (3<=p<=20) 그리고 다음 p 줄에는 다각형을 구성하는 x y 좌표가 순서대로 들어온다. 꼭지점의 좌표들은 모두 서로 값이 다르며 반시계 방향이다.

100 1
60 50
5
70 40
75 40
80 40
80 50
70 60

위의 예제의 (70, 40), (75, 40), (80, 40)처럼, 정점 좌표가 일직선 상에 있는 경우도 있을 수 있다.

출력 (boundary.out)

던이 그 위치에서 볼수 있는 말뚝의 개수를 한 줄에다 출력하면 된다. 위의 예제를 살펴보면, 농부는 (60, 50) 위치에 있는데 (70, 40) 위치의 바위 꼭지점 때문에 (100, 10)부터. 또 (70, 60) 위치의 바위 꼭지점 때문에 (100, 90)까지, 경계에 있는 81개의 말뚝이보이지 않게 된다. 따라서 정답은 400에서 81을 뺀 319이다.

319

비고

• 실행 제한: 실행 시간 1초, 메모리 제한 64MB
• 채점: 각 테스트 케이스마다 정답을 출력하면 만점을 받는다. 부분 점수는 없다.