 6
5
6
5
7 3
3 4
3 3
6 1
1 1
5 5
5 5
3 1제 17회는 2005년 8월 18일부터 25일까지 폴란드 Nowy Sącz에서 열렸다. 몇 년째 관례적으로 출제되던 제출형 문제가 나오지 않았다. 모든 문제들이 파일이 아니라 그냥 표준 입출력 스트림을 사용한다는 점, 그리고 대화형을 제외한 모든 문제들이 매 질문에 숫자 하나만 달랑 출력하는 형태라는 점에서, 문제 유형이 우리나라에서 열린 14회 때와 제법 닮았다. 더구나 기간까지 14회와 정확히 같아서 더욱 3년 전 기억을 되살린다. 휴리스틱, 부분 점수 문제가 없어지고, 최적해 문제도 "해가 여러 개 존재하더도 한 가지 경우만 출력하면 된다"란 꼬리표가 붙을 여지가 없도록 출력 형태가 단순하게 바뀌어 가니, 채점하기에는 편하겠다는 생각이 든다.
모든 문제에 등장하는 고유명사는 Byte- 접두사가 붙은 형태이다. 바이트만(Byteman, 사람 이름), 바이트랜드, 바이트타운 따위이다. 각 문제당 100점으로 총점 600점이었던 이번 대회에서 만점자는 4명이 나왔으며, 동메달 입상자의 최저 점수는 275점이었다.
원문이 있는 곳: http://www.ioi2005.pl/competition/tasks.php
바이트만은 바이트타운에서 가장 아름다운 정원을 소유하고 있다. 그는 정원에 n그루의 장미를 가꿨는데, 여름이 되어 장미들은 큼직하고 아름답게 자랐다. 그럴 즈음 그는 자기 힘으로 이 모든 장미들을 신경쓰기는 어렵다는 것을 느끼고, 정원사를 두 명 고용하여 이들에게 정원 관리를 돕게 하기로 했다. 정원 안에 직사각형 영역을 두 곳 만들어서 각 정원사가 자기가 맡은 영역 안의 장미를 책임지게 하는 것이다. 두 영역은 서로 겹쳐서는 안되며, 두 곳 모두 정확히 각각 k그루의 장미가 공평하게 내부에 있어야 한다.
바이트만은 정원사들이 일하는 두 영역 둘레에 울타리를 만들고 싶어한다. 그러나 그는 자금이 부족하기 때문에 울타리를 칠 영역을 무작정 넓게 잡을 수는 없다. 위의 조건을 만족하면서 가장 짧게 둘러쌀 수 있는 영역을 물색하고 있다. 당신은 이 일을 도와야 한다.
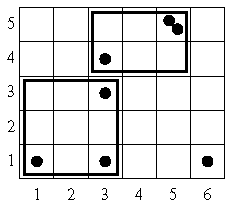
정원은 가로가 l미터, 세로가 w미터인 직사각형 모양이며, 가로· 세로가 1미터인 l×w개의 정사각형 칸으로 분할되어 있다. 정원은 x축과 y축에 평행하며, 만들고자 하는 두 내부 영역 역시 이 축을 따라 만든다. 정원 안의 모든 정사각형 칸은 1≤x≤l, 1≤y≤w를 만족하는 정수 좌표 (x, y)를 가지며, 각 칸에는 장미가 얼마든지 있을 수 있고, 또 없을 수도 있다. 우리가 선택하는 내부 영역 역시 (l1, w1), (l1, w2), (l2, w1), (l2, w2)를 모서리로 갖는 직사각형이라 표현할 수 있으며, 이 때 1≤ l1 ≤ l2 ≤l, 1≤ w1 ≤ w2 ≤w이다. 이 영역은 l1≤x≤l2, w1≤y≤w2를 만족하는 모든 칸 (x, y)를 포함하며, 둘레의 길이는 2×(l2-l1+1)+2×(w2-w1+1)과 같다.
두 정원사가 맡은 영역 사이에는 겹치는 칸이 없어야 한다. 그리고, 2번 칸 왼쪽과 1번 칸 오른쪽처럼 칸을 감싸는 둘레가 겹치는 곳이 있더라도 울타리는 따로 모두 만들어야 한다. 정원의 크기와 장미들의 위치, 그리고 정원사에게 할당하고 싶은 장미의 수를 입력받아, 최소한의 길이로 울타리를 치면서 장미도 지정해 준 대로 들어있는 두 영역을 구하는 프로그램을 작성하시오.
첫 줄에는 정원의 길이와 폭을 뜻하는 정수 l, w가 있다. (1≤ l, w ≤250) 둘째 줄에는 장미의 수 n, 그리고 정원사에게 할당할 장미 수 k가 있다. (2≤n≤5000, 1≤k≤n/2) 그리고 i+2째 줄에는 i째 장미가 있는 칸을 의미하는 두 정수 li, wi가 있다. (1≤li≤l, 1≤wi≤w) 한 칸에 두 그루 이상의 장미가 있을 수도 있다.
한편, 테스트 케이스의 절반은 정원의 크기 l, w가 40을 넘지 않는다.
 6
5
6
5
7 3
3 4
3 3
6 1
1 1
5 5
5 5
3 1
서로 겹치지 않고 영역 안에 정확히 k그루의 장미가 있으면서 둘레의 합이 최소인 두 영역을 구한 뒤, 그 영역의 둘레의 합을 출력한다. 만약 조건을 모두 만족하는 영역이 존재하지 않는 경우, NO를 출력한다. (메모리 제한: 32MB, 시간 제한: 0.5초)
22 (← 12+10)
오름차순 수열 s1, ..., sn+1 (1≤i≤n에 대해 si≤si+1)이 있다고 하자. 이에 대한 mi=(si+si+1)/2로 정의되는 수열 수열 m1, ..., mn을 s의 평균값 수열이라고 한다. 가령, 수열 1, 2, 2, 4의 평균값 수열은 1.5, 2, 3이다. 따라서 평균값 수열의 값은 분수가 될 수도 있지만, 이번 문제에서는 평균값이 정확하게 정수로 떨어지는 경우만을 생각하기로 한다.
n개의 정수로 된 오름차순 수열 m1, ..., mn이 있을 때, 이 m을 평균값 수열로 갖는 원래 수열 s1, ..., sn+1은 몇 개나 존재할지 그 개수를 계산하는 프로그램을 작성하시오.
첫째 줄에는 정수 n (2≤n≤5000000)이 있고, 다음에는 m1, ..., mn의 값을 의미하는 수가 한 줄에 하나씩 있다. (0≤mi≤10억) 단, 테스트 케이스들의 절반은 n≤1000이고 0≤mi≤20000이다.
3
2
5
9
평균값 수열이 입력으로 들어온 수열과 일치하는 원래 수열의 개수를 출력하면 된다. (메모리 제한: 16MB, 시간 제한: 5초)
4
2, 5, 9가 평균값 수열이 되는 오름차순 수열은 {2, 2, 8, 10}, {1, 3, 7, 11}, {0, 4, 6, 12}, {-1, 5, 5, 13} 이렇게 네 개가 존재한다.
어느 산악 유원지에서는 레일의 경사를 마음대로 조절할 수 있는 획기적인 스타일의 롤러 코스터를 선보였다. 롤러 코스터가 다니는 선로는 n개의 레일로 이루어져 있으며, 각 레일의 끝은 다음 레일의 시작과 연결된 형태이다. 첫 레일의 시작은 고도가 항상 0이나, 각 레일의 끝부분은 롤로 코스터 운영자인 바이트만이 높이를 얼마든지 조절할 수 있다. 레일의 시작과 끝의 높이가 다르면 롤러 코스터가 다니는 길에 경사가 생기는 것이다.
경사 조절은 이어져 있는 여러 레일을 상대로 일괄적으로 할 수 있다. 이 경우, 높이가 바뀐 레일의 바로 다음 레일들은 시작 부분이 이전 레일의 끝과 연결된 상태를 유지하게끔, 자신의 기울기(경사)는 유지한 채로 고도만 그대로 하강하거나 상승한다. 여기에 대해서는 입출력 예제에서 더 자세히 설명하기로 한다.
한편, 이 트랙을 다니는 열차는 고도가 0인 초기 위치에서 고도가 h인 지점까지 오를 수 있는 추진력을 한 번만 받은 후, 그 뒤부터는 그 높이에 다다르거나 레일을 모두 지날 때까지 관성으로 다닌다. 물론 레일에는 마찰이 없다고 가정한다.
초기에는 모든 레일들이 고도가 0인 위치에서 수평을 이루어 있다. 그러나 바이트만은 각 레일의 고도도 마음대로 조정하고, 그 상태에서 열차 운행도 초기 추진력을 무작위로 줘 가며 한다. 해당 상태에서 열차를 h까지 갈 수 있는 힘을 받아서 출발했을 때, 열차가 어느 레일까지 갈 수 있는지를 계산하는 프로그램을 작성하시오.
첫 줄에는 레일의 개수 n이 있다. (1≤n≤10억) 그리고 다음부터는 순차적으로 레일의 경사를 재조정하거나 그 상태에서 열차를 운행한 기록이 한 줄에 하나씩 들어있으며, 마지막으로 입력의 끝임을 나타내는 표시로 입력이 끝난다. 즉, 각 줄에는 다음 중 한 가지 형태의 정보가 있다.
경사를 조정하는 과정에서 레일 한쪽 끝의 고도 역시 0에서 10억 사이임이 보장된다. 또한 입력량은 10만 줄을 넘지 않는다. 테스트 케이스들의 절반은 1≤n≤20000이며, 입력량 역시 1000줄 이내이다.
4
Q 1
I 1 4 2
Q 3
Q 1
I 2 2 -1
Q 3
E
I 명령이 들어왔을 때 레일 상태의 변화를 잘 파악하고 있다가, Q 명령이 들어오면 그만한 힘을 받은 열차가 몇째 레일까지 완주할 수 있는지 계산하여 그 레일 번호를 출력하면 된다. (메모리 제한: 256MB, 시간 제한: 3초)
4
1
0
3
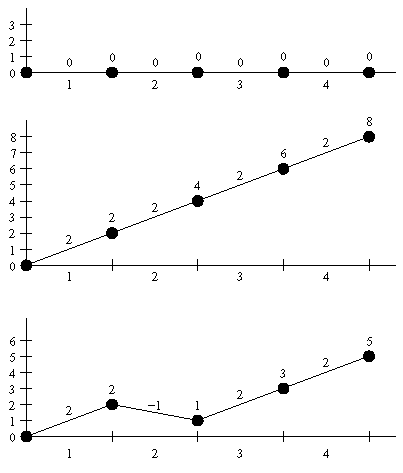
오른쪽 그림의 x축이 레일 번호를, y축은 고도를 뜻한다. 정점 위에 있는 수는 해당 레일의 시작/끝점의 고도이며, 선분 위에 있는 수는 그 레일의 경사이다.
초기에는 모든 레일이 경사가 없으므로 열차가 마지막 4번 레일까지 무난히 달릴 수 있다. 그러다가 1번부터 4번까지 2씩 경사가 생긴 뒤에는, 3이라는 고도까지 올라가는 힘으로는 2번 레일도 완주하지 못한다(끝의 고도가 4임). 그래서 둘째 출력값은 1이다. 하물며 1이라는 힘으로는 아무 레일도 갈 수 없기 때문에 셋째 출력값은 0이다. 끝으로 2번 레일의 경사를 2에서 -1로 설정하고 나면 3번과 4번 레일의 고도도 -3씩 감소하게 되고, 3이라는 힘으로 3번 레일까지는 갈 수 있게 되는 것이다.
오늘은 바이트만의 생일이다. 그래서 생일 잔치가 열렸고, 여기에는 바이트만 자신을 포함해 n명의 아이들이 초대되었다. 이들은 1부터 n까지 번호를 부여받아, n개의 의자가 마련된 커다란 원탁에 번호대로 시계 방향으로 돌아가며 앉았다. 즉, 1번 어린이가 가장 먼저 아무 자리에 앉고 나면, 2번 어린이는 1번의 왼쪽에 앉는다. 그리고 3번 어린이는 2번의 왼쪽에 앉으며, 이런 식으로 해서 맨 마지막 n째 어린이는 n-1번 어린이와 1번 어린이의 사이에 앉게 된다.
그런데 바이트만의 부모님은 이 아이들에 대해 아주 잘 안다. 어떤 아이들은 옆에 앉혀 놓으면 시끄럽게 떠들 거라는 걸 알기 때문에 그 상태에서 아이들의 자리 배치를 좀 바꾸고 싶어한다. 즉, 1부터 n까지 되어 있는 순서를 임의의 순열 p1, ..., pn (이들은 1부터 n까지의 제각기 서로 다른 정수)로 재조정해야 하는 것이다. 물론, 이 경우에도 2≤i≤n-1에 대해 pi번 어린이는 pi-1과 pi+1번 어린이 사이에 앉게 되고, pn번 어린이는 pn-1과 p1번 어린이 사이에 앉는 것을 의미한다. 단, 재배치 후 p1번 어린이는 pn번 어린이의 왼쪽에 있을 수도 있고, 오른쪽에 있을 수도 있다. 재배치 순서는 시계 방향이 되어도 좋고 반시계 방향이 되어도 좋다는 뜻이다.
재배치 방법은 간단하다. 이동해야 하는 아이들에게 새 자리를 알려 준 뒤, 이들이 동시에 일어나서 거기로 가서 앉게 하는 것이다. {1→2, 2→1}이라든가 {1→3, 3→4, 4→1}과 같은 식으로 말이다. 단, 자리 이동으로 인해 혼란이 야기되고 잔치 분위기를 망칠 수 있기 때문에 어떤 아이에 대해서든지 이동거리를 최소화해야 한다. 이 문제에서는, 본디 자리에서 가장 멀리 이동하는 아이의 이동거리를 분위기가 흐려지는 정도로 정의한다. 180도 반대편 자리로 가야 하는 아이가 생기는 게 최악의 상황인 것이다.
바이트만의 부모님은 한 아이에 대한 이동거리를 최소화하면서 자신이 원하는 대로 자리를 재배치하고 싶다. 부모님이 원하는 자리 배치 순서를 입력받아, 그렇게 재배치할 때 이론적으로 가능한 가장 작은 개인 이동거리를 계산하는 프로그램을 작성하시오.
표준 입력의 첫 줄에는 정수 n (1≤n≤100만)이 있고, 다음 줄에는 부모님이 원하는 어린이 배치 순서를 나타낸 1부터 n까지의 순열이 공백 한 칸으로 구분되어 있다. 단, 테스트 케이스의 절반은 n이 1000을 넘지 않는다.
6
3 4 5 1 2 6
원하는 대로 자리를 옮길 때 가장 멀리 이동해야 하는 아이의 거리의 최소값을 출력한다. (메모리 제한: 32MB, 시간 제한: 2초)
2
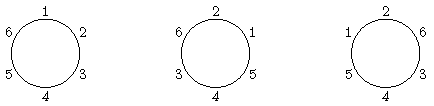
맨 왼쪽 그림은 자리를 바꾸기 전 아이들의 초기 자리 배치 모습이다. 그 상태에서 1번과 2번 아이가 각각 2번과 1번으로 이동하고, 3번과 5번 아이가 자리를 맞바꾸면 가운데 그림과 부모님이 원하는 형태의 배치가 만들어진다. 한편, 1, 2, 6번 아이가 각각 6, 1, 2번 자리로 가도 조건이 성립된다. 이번엔 방향이 반대이다. 여기서 한 가지 확실한 것은, 이렇게 아이들이 동시에 자리를 단 한 번 맞바꾸는 방법으로 "3 4 5 1 2 6"이란 배치를 만들려면, 어떤 아이는 원래 자리로부터 반드시 두 칸은 이동해야 하는 것이다.
직사각형 게임이란, x×y(x, y는 모두 양의 정수)크기의 직사각형을 두고 두 사람이 번갈아서 이것을 자르며 진행하는 게임이다. 차례가 된 사람은 사각형의 가로나 세로변과 평행한 방향으로 사각형을 완전히 잘라 두 동강을 낸다. 또한, 자르는 지점의 좌표도 정수여야 한다.
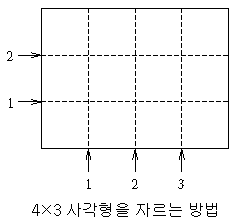
이렇게 해서 생긴 두 직사각형 중 넓이가 같거나 더 작은 하나는 버린 후, 남은 부위를 차례대로 또 같은 방법으로 자른다. 그렇게 게임을 진행해서, 더 쪼갤 수 없는 1×1 크기의 직사각형을 넘겨받은 사람이 게임에서 진다.
이런 규칙대로 직사각형 게임을 해서 이기는 프로그램을 작성하여라. 프로그램은 지정된 라이브러리와 교신하면서 게임을 한다. 라이브러리에는 초기 직사각형의 크기를 알려 주는 dimension_x()와 dimension_y() 함수를 제공하며, 직사각형 한 변의 초기 크기의 범위는 1 이상 10억 이하이다. 물론, 가로나 세로 중 1이 넘는 값은 반드시 존재한다. 또, 테스트 케이스들의 50%는 25를 넘지 않는 범위를 제시한다.
라이브러리에는 cut(dir, position)이라는 프로시저도 있다. 수험자의 프로그램이 자신의 직사각형 분할 동작을 라이브러리에 알려 줄 때 쓰는 함수이다. 매개변수 dir은 자르는 방향을 의미하며, 그 값은 vertical(세로) 아니면 horizontal(가로) 중 하나여야 한다. dir이 vertical이면 세로로 자르는 동작이 되어 position의 값은 1≤position≤dimension_x()-1을 만족해야 한다. 한편, dir이 horizontal이면 가로로 자르는 동작이 되어 1≤position≤dimension_y()-1이어야 한다.
프로그램이 시작되면 수험자의 프로그램부터 게임을 시작하여 직사각형의 적당한 곳을 잘라야 한다. 프로그램이 cut을 호출하면 그 동작이 기록되고, 게임 상대인 라이브러리도 그에 맞서 사각형을 자른 뒤 차례를 프로그램으로 넘겨 준다. 이 다음에 dimension_x()와 dimension_y()의 값을 살펴보면 자신과 라이브러리가 사각형을 어떻게 잘랐는지를 알고 이에 대처를 할 수 있다. 게임의 승패가 결정되거나 수험자의 프로그램이 잘못된 지시를 내리면(cut 함수에 넘겨주는 매개변수가 잘못된 경우) 프로그램은 즉시 종료된다. 이 과정은 채점 시스템에 의해 자동으로 진행되므로, 수험자는 프로그램의 종료에는 신경쓸 필요 없이 게임만을 진행하면 된다. 모든 테스트 케이스에는 게임을 먼저 시작하는 쪽에 대한 필승법이 존재한다고 가정한다.
이번에 작성하는 프로그램은 파일을 읽거나 쓰지도, 표준 입출력을 사용하지도, 프로세스 외부의 메모리에 접근하려 해서도 안된다. 이를 위반하는 행동이 감지된 프로그램은 실격 처리된다.
라이브러리의 동작을 익히면서 프로그램을 작성할 수 있게 하기 위해 예제 라이브러리가 소스 코드와 함께 제공되며(preclib.pas, creclib.c, creclib.h), 이들은 http://contest에서 받을 수 있다. 예제 라이브러리는 매우 단순한 방식으로 게임을 상대하며, 프로그램 테스트가 목적이라면 응시자 역시 라이브러리 소스를 얼마든지 고쳐서 빌드할 수 있다.
단, TEST 인터페이스로 제출한 답안 프로그램은 변경되지 않은 본디 예제 라이브러리로 빌드되며, 같이 제출한 입력 파일(직사각형의 초기 크기를 지정함)이 그대로 표준 입력을 통해 답안 프로그램으로 전달된다. 이 입력 파일에는 두 줄에 정수가 하나씩만 있어야 한다. 첫 줄은 가로, 다음 줄은 세로 크기가 들어있다. 예제 라이브러리는 이 파일을 읽어들인다.
예제 라이브러리의 파스칼 버전 소스를 고쳤다면, ppc386 -O2 preclib.pas 명령으로 재컴파일하도록 한다. 그 결과 preclib.o와 preclib.ppu가 생기며, 답안 프로그램을 빌드하는데 이 파일이 프로그램 디렉토리에 있어야 한다. 단, 인터페이스 부분은 고쳐서는 안된다.
예제 라이브러리의 C 버전 소스를 고쳤다면, creclib.* 파일을 답안 프로그램 디렉토리에 같이 두도록 한다. 컴파일할 때 필요하기 때문이다. 그러나 creclib.h는 고쳐서는 안된다.
그뿐만 아니라, 이 라이브러리를 사용한 예제 프로그램도 응시자의 편의를 위해 제공된다. 파일 이름은 crec.c, prec.pas이며, 이 코드는 다음 명령으로 빌드하면 된다.
gcc -O2 -static crec.c creclib.c -lm
g++ -O2 -static crec.c creclib.c -lm
ppc386 -O2 -XS prec.pas
단, 이 프로그램은 올바른 답안 프로그램이 아님을 명심하기 바란다.
이 문제에서 제공되는 라이브러리의 스펙은 다음과 같다.
프리파스칼용
type direction = (vertical, horizontal);
function dimension_x(): longint;
function dimension_y(): longint;
procedure cut(dir: direction; position: longint);
작성하는 rec.pas에는 uses preclib;를 삽입한다. 그리고 컴파일할 때는 preclib.o와
preclib.ppu를 답안 소스 코드가 있는 디렉토리로 복사한 뒤 다음 명령으로 컴파일한다.
ppc386 -O2 -XS rec.pas
라이브러리의 사용 예제가 prec.pas에 나와 있다.
GNU C/C++용
typedef enum __direction {vertical, horizontal} direction;
int dimension_x();
int dimension_y();
void cut(direction dir, int position);
작성하는 rec.c 또는 rec.cpp에 #include "creclib.h"를 삽입한다. 컴파일할 때는
creclib.c와 creclib.h를 답안 소스 코드가 있는 디렉토리로 복사한 뒤 다음 명령으로 컴파일한다.
gcc -O2 -static rec.c creclib.c -lm 또는 g++ -O2 -static
rec.cpp creclib.c -lm
라이브러리의 사용 예제가 crec.c에 나와 있다.
다음은 한 답안 프로그램이 평가 라이브러리와 교신하며 게임을 한 예이다. 게임은 4×3 크기에서 시작했으며, 이 경우 답안 프로그램이 이기는 방법이 존재한다.
| 라이브러리 함수 호출 | 일어나는 일 |
| dimension_x() | 함수값 4 |
| dimension_y() | 함수값 3 |
| cut(vertical, 1) | 세로로 1 잘린 사각형은 3×3이 되었고, 라이브러리는 가로로 또 잘라 이것을 3×2로 만들었다. |
| dimension_x() | 함수값 3 |
| dimension_y() | 함수값 2 |
| cut(horizontal, 1) | 가로로 1 잘린 사각형은 3×1이 되었고, 라이브러리는 세로로 또 잘라 이것을 2×1로 만들었다. |
| dimension_x() | 함수값 2 |
| dimension_y() | 함수값 1 |
| cut(vertical, 1) | 이 동작에 의해 사각형은 1×1이 되었다. 답안 프로그램이 이겼다. 프로그램은 자동으로 종료된다. |
메모리 제한: 32MB, 시간 제한: 14초 (평가 라이브러리가 소요하는 시간은 4초를 넘지 않는다고 가정할 것.)
바이트랜드 왕국은 거의 모든 지역이 강과 숲으로 이루어져 있다. 상류의 작은 강들은 모여서 큰 강이 되며, 그 강도 다른 강과 만나 더 커져 나중에는 하류로 가면 거대한 강 하나만이 남아 바이트타운 근처의 바다로 흘러간다.
바이트랜드에는 나무꾼들이 사는 n개의 마을이 강변에 있다. 그런데 현재는 목공소가 강의 최하류인 바이트타운에 하나만 있기 때문에, 제각기 사는 곳에서 나무를 벤 나무꾼들은 통나무를 강에다 띄워서 그 목공소로 보낸다. 그래서 바이트랜드의 왕은 통나무를 하류로 흘려보내는 물류비용을 줄이기 위해, 마을들 중 적당한 곳에 k개의 목공소를 더 짓기로 했다. 목공소가 더 생기면, 상류에서 흘러보낸 통나무들은 바이트랜드까지 갈 필요 없이 처음으로 거치는 목공소에서 바로 처리를 할 수 있으며, 목공소가 있는 마을에서 생산된 통나무는 강을 거칠 필요조차 없어진다.
목공소를 세울 곳을 결정하기 위해, 왕의 신하들은 각 마을별로 연간 생산되는 통나무의 양을 조사해 두었다. 강물은 하류로 갈수록 합쳐지기만 하지 갈라지지는 않기 때문에, 각 마을에서 바이트타운까지 가는 경로는 오직 하나만 존재한다. 마을별로 강을 이용해 이웃 마을이나 현재의 최종 목적지인 바이트타운까지 가는 거리에 대한 자료 역시 있다. 이것을 토대로, 전국의 나무의 물류비용을 최소화하려면 어디에 목공소를 건설하면 좋을지 결정하는 프로그램을 작성하시오. 통나무 하나를 강으로 1km 거리만치 운반하는데 드는 비용은 1로 한다.
첫 줄에는 바이트타운을 제외한 마을의 수 n과 추가로 지으려고 하는 목공소의 수 k가 있다. (2≤n≤100, 1≤k≤50이고 k≤n) 마을들은 1부터 n까지 번호가 부여되어 있으며, 바이트타운의 번호는 0이다.
그리고 다음에는 n개의 줄이 더 있으며, i+1째 줄에는 각 마을에 대한 정보를 의미하는 세 개의 정수가 있다.
마을 전역에서 생산되는 통나무들을 바이트타운까지 운반하는데 드는 비용의 합은 20억을 넘어가지 않는다고 가정한다. 한편, 테스트 케이스들의 절반은 n의 값이 20을 넘지 않는다.
 4
2
4
2
1 0 1
1 1 10
10 2 5
1 2 3
목공소를 최적의 위치에다 지었을 때, 마을 전역에서 생산되는 통나무를 "적당한 목공소가 있는 곳"까지 강으로 운반하는데 드는 최소 비용을 출력한다. (메모리 제한: 32MB, 시간 제한: 1초)
4
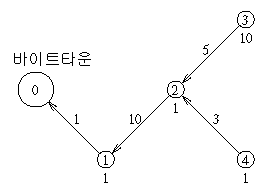
위의 그림에서 선분은 강을 뜻하고, 원으로 된 정점은 마을을 뜻한다. 선분 위의 숫자는 해당 구간의 거리이며, 원 안의 숫자는 마을 번호, 그리고 원 아래의 숫자는 그 마을에서 매년 생산되는 통나무의 수이다.
이 예제에서 목공소를 지어야 하는 최적의 위치 두 곳은 2번과 3번 마을이다. 이 경우 4번 마을의 통나무를 2번 마을로 보내는 비용 1×3과, 1번 마을의 통나무를 바이트타운으로 보내는 비용 1×1만이 필요하다.