제 18회

제 18회는 2006년 8월 13일부터 20일까지 멕시코 Mérida에서 열렸다. 이번 대회에서는 처음으로 윈도우 운영체제의 지원이 중단되었다.

제출형만이 부분점수이고 나머지는 모두 최적해만을 인정하는 문제이다. 1번은 11회의 2번 암호 찾기와 유사한 문자열 응용 검색이고 2번은 11회의 6번 비행장 부지 찾기와 비슷한 타입의 문제이다. 3번은 16회의 3번과 비슷하게 NP 완전 문제를 변형하여 제출형으로 만든 것이다.

4번은 13회 KOI 고등부에 출제되었던 "교차하지 않는 현의 최대 집합" 문제와 비슷하다. 5번은 상당히 기발하게 느껴진 기하학 문제이고 6번은 기본적으로는 제출형이지만 대화형의 성격도 상당 부분 띠고 있어 독특하다.

600점 만점에 금메달 입상자의 최고 점수는 480점, 동메달 입상자의 최저 점수는 219점이었다. 우리나라는 금메달 1개, 은메달 3개를 획득했다.

원문이 있는 곳: http://www.ioi2006.org/index.php?page=tasks&menu=0010

1. 문자 해독

2. 피라미드

3. 금지된 부분그래프 (제출형)

4. 멕시코 계곡

5. 점 잇기

6. 블랙박스 게임 (제출형)

1. 문자 해독

마야 문자를 해독하는 일은 예상 외로 어려운 일임이 밝혀져 있다. 거의 200년이 지난 뒤에도 뜻이 완전히 밝혀진 것은 거의 없는 실정이며, 그나마 해독에 이렇다할 진척이 시작된 지는 오늘날로부터 30여 년밖에 되지 않았다.

마야 문자는 소리를 나타내는 여러 종류의 그림글자로 구성되는데, 이 글자들이 여러 위치에서 결합함으로써 단어를 형성한다.

마야 문자 해독을 어렵게 하는 요인 중 하나는 바로 단어를 읽는 순서이다. 마야 문자를 쓰는 고대인들은 단어를 기록할 때 특정한 규칙 대신, 그들이 보기에 좋게 보이도록 단어를 이루는 글자들을 아무렇게나 배열했다. 그렇기 때문에 고고학자들이 마야 기록에서 단어를 이루는 각 그림글자들의 발음을 알아 내더라도 그 단어를 실제로 발음하는 방법은 정확히 알 수 없는 셈이다.

고고학자들은 W라는 특정 단어를 발굴 기록으로부터 찾고 있다. 그 단어를 구성하는 각 글자들은 무엇인지 알고 있지만, 이것이 고대 기록에 어떤 형태로 숨어 있는지는 다 알지 못한다. 그런데 마침 '06년도 IOI가 멕시코에서 열린다는 것을 안 그들은 여러분에게 도움을 청했다.

그들은 W를 이루고 있는 g개의 그림문자와, 연구 대상인 벽화에 기록된 마야 문자열 S를 넘겨 줄 것이다. 단어 W가 S에 들어있을 수 있는 모든 가짓수를 계산하는 프로그램을 작성하시오. 즉, 문자열  S안에서 문자열 W의 순열 중 하나가 substring으로 들어있는 모든 경우의 수를 계산하라는 뜻이다.

입력 (writing.in)

첫째 줄에는 고고학자들이 찾고자 하는 단어 W의 길이 g와(1≤g≤3000), 발굴된 벽화에서 추출한 문자열 S의 길이 |S|가 공백으로 구분되어 들어있다. (g≤|S|≤3000000)

그리고 둘째 줄에는 g, 그리고 셋째 줄에는 S의 실제 내용이 들어있다. 모든 문자열은 a~z, 또는 A~Z 중 하나인 알파벳만으로 이루어져 있으며, 대소문자를 구분한다.

4 11
cAda
AbrAcadAbRa

총합 50점에 해당하는 테스트 케이스들은 g≤10을 만족하는 작은 데이터이다.

출력 (writing.out)

W의 순열이 S 안에 있을 수 있는 형태의 개수를 한 줄에다 출력한다. (메모리 제한: 32MB, 시간 제한: 3초)

2

cAda라는 단어는 AbrAcadAbRa 또는 AbrAcadAbRa라는 두 가지 형태로 존재할 수 있다.

파스칼 이용 시 유의사항

FreePascal은 기본적으로 string 타입의 문자열 최대 길이를 255자로 제한하고 있다. 그보다 긴 문자열을 다루고 싶으면 program ...; 문 바로 아래에 {$H+} 지시자를 넣도록 한다.

2. 피라미드

큰 전투에서 승리한 후 재규어 왕은 기념비 역할도 하고 전몰 용사들의 무덤 역할도 할 피라미드를 하나 건축하기로 작정했다. 피라미드는 전쟁터에 세워지며 가로로 a칸, 세로로 b줄인 직사각형 형태로 면적을 차지한다. 또한 피라미드 안에는 가로로 c칸, 세로로 d줄인 작은 방을 하나 만들어 전사자들의 시신과 유품 무기를 안치할 예정이다.

왕의 건축가들은 전쟁터의 지형을 가로로 m칸, 세로로 n칸인 직사각형 격자로 나누고, 각 정사각형 칸의 고도를 정수로 측량해 냈다. 피라미드와 내부 방은 모두 이 격자의 칸에 정확히 맞춰진 형태로 지을 것이다. 내부 방이 차지하는 칸은 고도를 바꿀 수 없지만, 그 외에 피라미드의 터가 차지하는 칸들은 본격적인 건축 작업을 위해 고도를 평준화하게 된다. 즉, 높은 곳의 모래를 낮은 곳에다 부어서 모든 칸들의 고도를 고도의 전체 평균값으로 바꾼다. (물론 방이 차지하는 칸의 고도는 제외한 평균) 방은 크기만 정해져 있기 때문에, 사방으로 피라미드와 외부 사이에 한 칸 이상의 간격만 확보된다면, 피라미드 내부의 어느 위치에다 만들어도 괜찮다. (꼭 중심부가 아니어도 됨)

건축가들은 피라미드를 전쟁터의 어디에다 짓고 내부 방은 그 안의 어디에다 만들면, 피라미드 터의 최종 평균 고도가 가장 높아질 수 있는지 이를 찾는데 고심하고 있다. 이번 문제는 그들을 돕는 것이다. 전쟁터, 피라미드, 내부 방의 크기와 전쟁터 각 칸의 고도를 입력 받은 후, 터의 평균 고도를 최대화할 수 있는 피라미드와 방 위치를 계산하는 프로그램을 작성하시오.

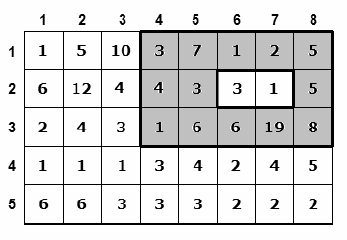
오른쪽의 그림은 전쟁터의 한 예이다. 각 칸의 숫자들은 전쟁터의 위치별 고도이다. 그리고 회색 영역은 피라미드가 지어질 터이며, 그 안의 흰색 영역은 내부 방이 들어가는 공간이다. 전쟁터의 크기와 고도 정보가 그림과 같고, 만들고자 하는 피라미드와 방의 크기와 그림과 같을 때, 위치도 그림과 같이 선정하는 것이 고도를 최대화할 수 있다.

입력 (pyramid.in)

첫째 줄에는 여섯 개의 정수 m (3≤m≤1000), n (3≤n≤1000), a (3≤a≤m), b (3≤b≤n), c (1≤c≤a-2), d (1≤d≤b-2)가 있다. 그리고 다음 n개의 줄에는 왼쪽부터 오른쪽으로 그 줄에 해당하는 칸의 고도를 나타내는 m개의 정수가 들어있다. 고도의 범위는 1 이상 100 이하이다.

8 5 5 3 2 1
1 5 10 3 7 1 2 5
6 12 4 4 3 3 1 5
2 4 3 1 6 6 19 8
1 1 1 3 4 2 4 5
6 6 3 3 3 2 2 2

총합 30점에 해당하는 테스트 케이스들은 3≤m≤10, 3≤n≤10을 만족하는 작은 데이터이다.

출력 (pyramid.out)

첫 줄에는 피라미드를 지을 터의 좌측 상단 위치를 가로-세로 형태로 출력하고, 둘째 줄에는 방의 좌측 상단 위치를 가로-세로 형태로 출력한다. 모든 좌표는 1부터 시작한다. 최적해가 여러 개 존재하더라도 그 중 하나만 출력하면 된다. (메모리 제한: 32MB, 시간 제한: 1초)

4 1
6 2

3. 금지된 부분그래프

무방향 그래프 G와 H가 있고 서로 다음과 같은 조건을 만족한다면, 이들은 동형(isomorphic)이라고 한다.

• 정점의 수가 서로 같다.
• G 내부의 임의의 두 정점에 대해 연결된 선분은 H에 대해서도 그에 해당하는 두 정점이 선분으로 연결된 것을 찾을 수 있으며, 이들이 필요충분관계가 성립한다.

예를 들어 아래의 두 그래프는 생김새는 다르지만 서로 동형이다.

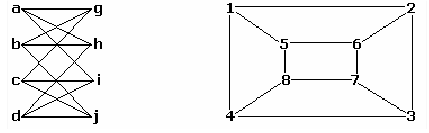
a↔1, b↔6, c↔8, d↔3, g↔5, h↔2, i↔4, j↔7과 같은 방법으로 그래프의 정점을 치환해 보면 두 그래프의 위상이 동일하다는 것을 알 수 있으며, 치환 방법은 이것 말고도 다른 방법이 얼마든지 존재할 수 있다.

그래프 G의 부분그래프란 정점과 선분이 G의 부분집합으로 완전히 속해 있는 그래프를 말한다. G는 G 자신의 부분그래프가 될 수 있다. 다음은 그래프와 그 그래프의 부분그래프의 한 예이다.

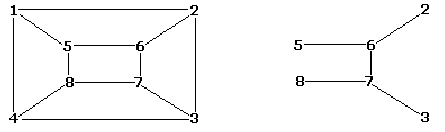
그리고 그래프 G의 부분그래프 중 하나인 H'가 그래프 H와 동형인 경우, G는 H를 포함한다고 말한다. 다음은 그래프 G가 그래프 H를 포함하고 있음을 보이는 예이다.

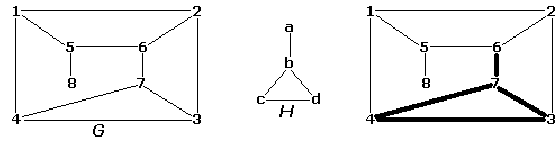
무향 그래프 G와 H에 대한 정보를 토대로, G와 정점 수는 같으면서 H가 포함되어 있지 않은 G의 부분그래프 G'를 찾아 제출하시오. 이런 조건을 만족하는 G'는 여러 가지가 있을 수 있다. 그 중에서 선분이 가장 많이 남아 있는(= G의 원형을 최대한 보존한) G'를 찾아야 한다.

기본 알고리즘

이 문제를 풀기 위해 가장 직관적으로 떠올릴 수 있는 방법은, G를 이루고 있는 선분을 순서대로 하나씩 G'에다 추가하면서 H가 G'에 속하게 되는지를 매번 점검하는 것이다. 이 그리디 알고리즘만 제대로 구현해도 점수를 일부 얻을 수는 있다. 그러나 훨씬 더 좋은 전략이 있으므로 이 문제를 완전히 풀기 위해서는 그 방법을 찾아야 한다.

입력 (forbiddenK.in)

수험자는 forbidden1.in부터 forbidden10.out까지 10개의 다각형 정보를 받는다. 그 구조는 다음과 같다.

첫째 줄에는 그래프 H의 정점 수 m (3≤m≤4)과 그래프 G의 정점 수 n (3≤n≤1000)이 있다. 다음 m개의 줄에는 줄마다 m개의 숫자가 있어서 그래프 H의 각 정점별로 다른 정점과의 선분 연결 여부가 들어있다. 1은 연결됨을, 0은 연결되지 않음을 뜻한다. 그리고 다음 n개의 줄에는 줄마다 n개의 숫자가 있어서 그래프 G의 각 정점별로 다른 정점과의 선분 연결 여부가 들어있다.

i째 줄에 있는 j째 칸의 숫자는 정점 i와 정점 j 의 연결 여부이며, 결국 첫째 줄 이후에 들어오는 정보는 그래프 H와 G의 인접 행렬(adjacency matrix)임을 알 수 있다.

3 5
0 1 0
1 0 1
0 1 0
0 1 0 0 0
1 0 1 0 0
0 1 0 1 0
0 0 1 0 1
0 0 0 1 0

출력 (forbiddenK.out)

각 입력 파일별로 출력 파일도 10개를 만들어 제출한다. 첫째 줄에는 답안 번호를 나타내는 헤더인 "FILE forbidden K"를 넣는다. K는 1~10 사이의 답안 번호이다. 둘째 줄에는 G'의 정점 수 n을 출력한다.

그리고 다음 n개의 줄에는 수험자가 구한 G'의 구조를 나타내는 인접 행렬을 입력 파일 구조와 동일한 형태로 출력한다. i째 줄에 있는 j째 칸의 숫자는 정점 i와 정점 j의 연결 여부로, 1은 연결됨을, 0은 연결되지 않음을 뜻한다.

#FILE forbidden K
5
0 1 0 0 0
1 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0

선분이 가장 많으면서 문제의 조건을 만족하는 부분그래프는 여러 개가 있을 수 있으나 하나만 출력하면 된다. 위의 입력에 대한 이 출력은, 조건을 만족하는 바른 답이기는 하지만 최적해는 아니다.

채점

답안으로 제출한 그래프는 먼저 문제의 조건을 만족해야 한다. (그렇지 못하면 0점) 바른 답안이라면 그 그래프의 선분의 개수에 따라 다음과 같이 점수가 매겨진다. 수험자가 제출한 답안 그래프의 선분의 개수를 E_y, "기본 알고리즘"으로 구한 그래프의 선분 개수를 E_b, 그리고 전체 수험자 중 선분을 가장 많이 남긴 최적해의 선분 개수를 E_m이라 할 때,

• E_y ≤ E_b이면, 즉 결과가 기본 알고리즘보다 나은 게 없으면 30×E_y/E_b (즉, 아무리 잘 해 봐야 100점 만점에 30점밖에 못 받음)
• 그렇지 않으면 30+70(E_y-E_b)/(E_m-E_b)

4. 멕시코 계곡

멕시코의 수도인 멕시코시티는 멕시코 계곡라는 아름다운 계곡에 건설되어 있는데, 이곳은 오래 전에는 모두 호수였다. 1300년대에는 이곳에 산 아즈텍 인의 종교 지도자들이 모여서, 호수의 중앙을 메우고 그 위에 도읍을 건설하자고 결정하기도 했다. 그러던 것이 지금은 호수가 모두 뭍으로 변해 버렸다.

아즈텍 인들이 정착하기 전에는 호수의 기슭에 c개의 도시가 자리잡고 있었다. 그리고 이들 중 일부는 서로 무역 협정을 맺었으며, 협정이 체결된 도시들끼리 배를 타고 호수를 직선 거리로 왕래하면서 물자를 교류했다.

그러던 것이 각 도시의 대표들이 모여 이 무역 경로를 조직화하기로 결정했다. 무역 협정이 체결된 도시 사이의 경로들만 선택하여 모든 도시를 연결하는 통합 경로를 선정하는 것이다. 이 통합 경로는 다음과 같은 조건을 만족해야 한다.

• 임의의 도시에서 시작하여 호수 기슭의 모든 도시들을 한 번씩 방문한 후, 시작 도시가 아닌 다른 도시에서 끝난다.
• 도시와 도시 사이를 오갈 때는 무역 협정이 맺어진 도시 사이의 경로만을 택해야 하는데, 어떤 경로를 한 번 지나고 나면 그 경로는 선으로 그어진다.
• 예전의 방문에 의해 선으로 그어져 버린 구간을 또 지나서는 안 된다. 배들 사이의 충돌을 막기 위한 조치이다.

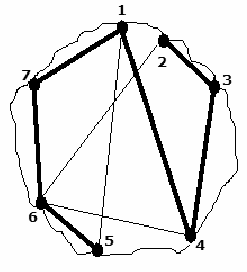
오른쪽 그림은 호수와 그 기슭의 도시들을 나타낸 것이다. 선(굵은 것과 가는 것 모두)으로 연결된 도시는 무역 협정이 맺어진 도시를 나타낸다. 그리고 굵은 선은 위의 조건을 만족하는 통합 경로를 나타낸다. 2번에서 시작해서 5번으로 끝나며, 모든 도시들을 한 번씩 지나고 자신의 경로와 스스로 교차하는 일도 없다.

그 반면 2→6→5→1번과 같은 순서대로 경로를 짠다면 2-6과 1-5 선분 사이에 교차가 발생하고 통합 경로의 조건과 어긋나게 된다.

도시들은 1부터 c까지 시계 방향으로 번호가 매겨져 있다. 도시의 개수와 각 도시들의 무역 협정 관계를 입력 받아, 위의 조건을 만족하는 통합 경로를 구하는 프로그램을 작성하시오.

입력 (mexico.in)

첫째 줄에는 도시의 개수 c (3≤c≤1000)가 있고, 다음 줄에는 무역 협정의 전체 건수(선분 개수)를 나타내는 정수 n이 있다. 그리고 다음 n개의 줄에는 협정이 맺어진 두 도시의 번호가 들어있다. (각 숫자의 범위는 1~c이며, 각 줄에서 두 숫자의 출현 순서는 중요하지 않다.)

7
9
1 4
5 1
1 7
5 6
2 3
3 4
2 6
4 6
6 7

총합 40점에 해당하는 테스트 케이스들은 3≤c≤20을 만족하는 작은 데이터이다.

출력

통합 경로를 구하여 순회하는 순서대로 도시의 번호를 한 줄에 하나씩 총 c줄을 출력한다. 통합 경로가 존재하지 않는 케이스라면 -1 한 줄을 출력한다. (메모리 제한: 16MB, 시간 제한: 0.75초)

2
3
4
1
7
6
5

5. 점 잇기

"점 잇기"란 혼자서 하는 게임을 가리키는 말이다. 이 게임은 2보다 큰 두 정수 g, r을 설정하고서 시작한다. 정사각형을 이루는 네 점을 찍되 윗변을 이루는 점은 초록색으로, 아랫변을 이루는 점은 빨간색으로 찍는다. 그러고 나서 이 정사각형의 영역 안에 초록색 점과 빨간색 점을 찍는데, 이미 그린 정사각형의 가장자리 점을 포함하여 어떤 세 점도 한 직선 위에 있지 않도록 유의한다. 이렇게 해서 가장자리를 포함한 초록색 점 g개, 빨간색 점 r개를 모두 찍으면 게임판이 완성된다.

게임의 진행은 간단하다. 색깔이 같은 점들을 그 색으로 직선을 그어 연결한다. 단, 새로 긋는 선이 이미 그어진 선과 도중에 마주쳐서는 안 되고 언제나 끝점과만 연결되어야 한다.

두 점 u와 v가 그렇게 연결된 선을 통해서 상호 왕래가 가능할 때, 이 두 점은 서로 일체라고 하자. 점 잇기 게임의 성공 조건은 다음과 같다. 점들을 잘 연결하여 초록색 점은 g-1개의 선으로 모든 점이 일체가 되도록 하고, 빨간색 점은 r-1개의 선으로 모두 연결하여 빨간 점들끼리 또 일체가 되게 하는 것이다. 물론 도중에 마주치는 선들이 전혀 없이 말이다. 점들을 위의 제시 조건대로만 찍었다면, 이를 색깔별로 그렇게 성공적으로 연결시키는 방법은 반드시 존재함이 증명되어 있다.

이 문제에서는 게임판의 최대 크기인 s, 그리고 초록색 점의 개수 g와 빨간색 점의 개수 r이 주어지며 각 점의 좌표는 정수쌍 (x_i, y_i)로 표현된다. 초록색 점은 1부터 g까지 번호가 매겨지며 좌측 상단인 1번 점의 좌표는 (0, s)이고 우측 상단인 2번 점의 좌표는 (s, s)이다. 그리고 3번부터 g번 점은 임의 순서이다. 빨간색 점은 1부터 r까지 번호가 매겨지며 좌측 하단인 1번 점의 좌표는 (0, 0)이고 우측 하단인 2번 점의 좌표는 (s, 0)이다. 그리고 3번부터 r번 점은 임의 순서이다.

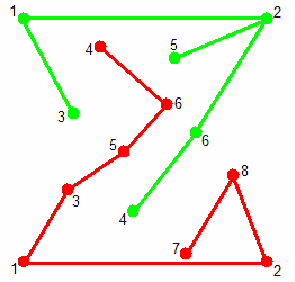
오른쪽의 그림은 초록색 점과 빨간색 점을 모두 일체로 연결하여 게임을 성공한 예이다. 어떤 세 점도 일직선상에 있지 않으며 끝점을 제외하면 두 직선이 한 점에서 만나는 경우도 없음을 알 수 있다. 점 잇기 게임을 성공하도록 점을 잇는 방법을 찾는 프로그램을 작성하시오.

입력 (points.in)

첫째 줄에는 g의 값이 있고 다음 g개의 줄에는 1번부터 g번 초록색 점의 좌표 (x_i, y_i)가 들어있다. 그리고 g+2째 줄에는 r의 값이 있고 다음 r개의 줄에는 1번부터 r번 빨간색 점의 좌표 (x_i, y_i)가 들어있다.

6
0 1000
1000 1000
203 601
449 212
620 837
708 537
8
0 0
1000 0
185 300
314 888
416 458
614 622
683 95
838 400

총합 35점에 해당하는 테스트 케이스들은 3≤g≤20, 3≤r≤20을 만족하는 작은 데이터이다.

출력 (points.out)

선으로 연결할 점의 번호를 먼저 출력하고, 이 점이 초록색 점을 가리키면 g를, 빨간색 점이면 r을 덧붙인다. 총 (g-1) + (r-1)줄을 출력하면 되며, 색깔이나 번호별로 점을 연결하는 순서라든가 한 선분에서 먼저 출력할 점의 번호는 신경쓸 필요 없다. (메모리 제한: 32MB, 시간 제한: 1초)

1 3 g
3 1 r
3 5 r
4 6 r
6 5 r
4 6 g
1 2 g
1 2 r
5 2 g
2 6 g
7 8 r
8 2 r

6. 블랙박스 게임

블랙박스 게임은 평면 위에 놓인 정사각형 모양의 블랙박스를 조작하는 게임이다. 블랙박스의 각 네 변에는 n개의 구멍이 있어서 (따라서 총 4n 개의 구멍이 존재) 여기로 공을 던져 넣을 수 있다. 들어간 공은 4n개의 구멍 중 하나로 빠져나오며, 들어갔던 구멍으로 다시 나올 수도 있다.

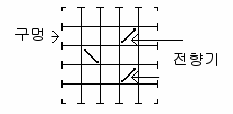
이 블랙박스의 내부는 n×n개의 칸으로 구성된 격자라고 볼 수 있다. 겉에 있는 구멍들은 가로· 세로의 양 끝을 의미한다. 박스 내부의 각 칸들은 비어 있거나 전향기라는 장치가 차지하고 있다. 전향기는 던져진 공의 진행 방향을 90도 돌리는 역할을 한다. 오른쪽 그림과 같은 5×5 크기의 한 블랙박스를 생각해 보자.

박스 내부로 던져진 공은 전향기를 만나거나 다른 쪽 끝으로 나갈 때까지 직진한다. 전향기에 부딪힌 공은 진행 방향이 바뀌는데, 이때 전향기도 전향 방향이 ↖, ↙가 번갈아가며 바뀐다. 이것을 보여주는 예는 아래와 같다.

1. 공이 블랙박스 안으로 들어왔다가 전향기를 만나 진행 방향이 바뀌었다.
2. 먼젓번 공의 영향으로 전향기 역시 전향 방향이 바뀌었다. 그래서 다음에 들어오는 공은 똑같은 방향으로부터 와서 같은 전향기를 만났지만 먼젓번 공과는 정반대 방향으로 나갔다.
3. 공을 두 번 상대한 전향기는 상태가 두 번 바뀜으로써 이전 상태로 되돌아갔다.

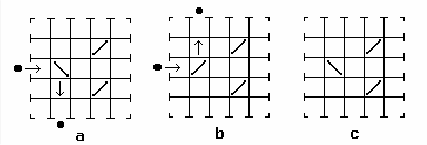
공이 전향기와 부딪히면 블랙박스 내부에서 경보음이 난다. 그래서 경보음이 들린 횟수를 세면 공이 전향기와 몇 번 만났는지를 알 수 있다. 외부에서 들어온 공은 무한 순환 없이 블랙박스 밖으로 반드시 빠져나간다는 것을 증명할 수 있다. 박스에는 모든 전향기의 상태(=전향 방향)를 공이 들어가기 전의 초기 상태로 되돌리는 버튼이 있으며, 모든 전향기들의 상태(↖, ↙)를 맞바꾸는 버튼도 갖추고 있다.

수험자에게는 파스칼이나 C/C++ 함수를 통해 15개의 서로 다른 블랙박스에 접근하는 인터페이스가 부여될 것이다. 이를 토대로 각 블랙박스의 내부가 어떠할지(박스 어디에 초기 상태가 어떠한 전향기가 존재하는지)를 최대한 자세히 알아내어 그 결과를 제출하시오. 수험자가 직접 만든 블랙박스를 대상으로 프로그램을 테스트하는 방법도 제공될 것이다. (1≤n≤30)

출력 (blackboxK.out)

15개의 블랙박스별로 내부 구조도를 나타내는 출력 파일을 따로 제출한다. 첫째 줄에는 답안 번호를 나타내는 헤더인 "FILE blackbox K"를 넣는다. K는 1~15 사이의 답안 번호이다.

그리고 다음 n개의 줄에는 맨 위부터 아래까지 블랙박스 각 줄의 구조를 넣는다. 한 줄에는 정확히 n개의 문자가 있어야 하며, 각 문자가 각 칸에 대응한다. 들어갈 수 있는 문자는 빈 칸을 의미하는 마침표, 초기 상태가 ↙인 전향기를 의미하는 /, 초기 상태가 ↖인 전향기를 의미하는 \, 그리고 상태를 판단할 수 없음을 의미하는 ? 중 하나이다.

#FILE blackbox K
.....
.../.
.\...
.../.
.?.?.

라이브러리

이 문제를 풀기 위해 다음과 같은 함수들이 라이브러리로 제공된다.

function Initialize(box: integer): integer;
int Initialize(int box);

라이브러리를 초기화하는 함수로, 프로그램을 시작할 때 반드시 호출해야 한다. box는 사용자가 문제를 풀기 위해 접근하고자 하는 블랙박스의 번호로 1~15중 하나를 넣으면 된다. 한편, 0을 지정하면 라이브러리는 사용자가 파일로 지정한 블랙박스를 읽어들인다.

function throwBall(holeIn, sideIn: ineger; var holeOut, sideOut: integer): longint;
int throwBall(int holeIn, int sideIn, int *holeOut, int *sideOut);
int throwBall(int holeIn, int sideIn, int &holeOut, int &sideOut);

공을 사각형의 네 변 중 한 변(sideIn)에 있는 holeIn째 구멍으로 던져 넣는다. 변의 위치를 나타내는 번호는 1이 위, 2는 오른쪽, 3은 아래, 4는 왼쪽이다. 그리고 구멍의 번호는 왼쪽에서부터 1이고 위에서부터 1이며, n까지 순서가 매겨져 있다. 함수 호출이 끝나면 공이 빠져나온 변의 위치가 sideOut에, 그리고 그 변의 구멍 번호가 holeOut에 되돌려지며, 경보음이 들린 횟수를 자체 리턴값으로 추가로 알려 준다.

procedure ResetBox;
void ResetBox();

상자 안의 모든 전향기의 상태를 초기화한다.

procedure ToggleDeflectors;
void ToggleDeflectors();

상자 안의 모든 전향기의 전향 방향을 맞바꾼다.

procedure Finalize;
void Finalize();

블랙박스와의 교신을 마친다. 수험자의 프로그램 실행이 끝날 때 호출되어야 한다.

라이브러리를 쓰려면 언어별로 다음과 같은 처리를 하면 된다.

• FreePascal: 수험 디렉토리에는 pbblib.o와 pbblib.ppu가 있으며, 수험자의 코드에 uses pbblib; 를 추가하면 이를 사용할 수 있다. 라이브러리의 사용 예제로 pblackbox.pas 코드가 제공된다.
• C: 수험 디렉토리에는 cbblib.o와 cbblib.h가 있으며, 수험자의 코드에 #include "cbblib.h"를 추가하면 이를 사용할 수 있다. 라이브러리의 사용 예제로 cblackbox.c 코드가 제공되며, 라이브러리를 사용한 코드를 컴파일하려면 다음과 같은 명령을 내리면 된다.
  gcc -o yourprogram cbblib.o yourprogram.c
• C++: 수험 디렉토리에는 cppbblib.o와 cppbblib.h가 있으며, 수험자의 코드에 #include "cppbblib.h"를 추가하면 이를 사용할 수 있다. 라이브러리의 사용 예제로 cppblackbox.cpp 코드가 제공되며, 라이브러리를 사용한 코드를 컴파일하려면 다음과 같은 명령을 내리면 된다.
  g++ -o yourprogram cppbblib.o yourprogram.cpp

주의: 본 라이브러리를 사용하는 프로그램은 한 번에 하나만 실행될 수 있다.

교신 예제

• Initialize(0); 라이브러리가 사용하는 블랙박스가 앞에서 제시한 예제와 같다고 가정하자. 이 경우 함수의 리턴값은 블랙박스의 크기인 5이다.
• throwBall(3, 4, holeOut, sideOut); 공을 왼쪽 변(4의 의미)에서 위로부터 셋째 위치에 있는 구멍으로 던져 넣었다. 함수의 리턴값은 1로, 이는 공이 전향기를 한 번 만났음을 의미한다. 함수 실행이 끝나면 holeOut은 2로, sideOut은 3으로 설정되어 있으며, 이는 공이 아래쪽 변에서 왼쪽으로부터 둘째 위치에 있는 구멍으로 빠져나왔음을 뜻한다.

실험해 보기

Initialize 함수의 인자로 0을 지정하면 라이브러리는 사용자가 지정해 준 blackbox.in이라는 파일로부터 블랙박스 내용을 읽어들인다. 이렇게 하면 수험자는 자신만의 블랙박스로 라이브러리의 동작을 실험해 볼 수 있다.

blackbox.in의 첫 줄에는 블랙박스의 크기(=한 변의 구멍 수)를 의미하는 n이 들어가고, 다음 줄에는 상자 안에 있는 전향기의 전체 개수가 들어간다. 그리고 다음 d개의 줄에는 전향기의 가로, 세로 위치와 초기 상태가 있다. 아래의 예제는 위의 블랙박스의 상태를 기술한 것이다.

5
3
2 3 \
4 2 /
4 4 /

에러 메시지

라이브러리를 사용하는 도중에 비정상적인 상황이 발생하면 라이브러리는 표준 에러 스트림으로 에러 메시지를 출력한다. 다음은 발생할 수 있는 에러의 예이다.

• ERR 1: 블랙박스 라이브러리를 사용하는 프로그램은 한 번에 하나밖에 실행될 수 없다. 모든 프로그램들을 종료하고 하나만 다시 실행하기 바란다.
• ERR 2: 초기화할 때 지정해 준 블랙박스의 번호가 0~15 사이에 있지 않다.
• ERR 3: blackbox.in에 명시되어 있는 전향기의 위치가 잘못되었다. (범위 초과 등)
• ERR 4: blackbox.in에 형식에 어긋난 문자가 있다. (/ \ 외의 상태 등)
• ERR 5: blackbox.in에 명시된 블랙박스의 크기가 잘못되었다.
• ERR 6: 공을 던지라고 지시한 구멍 번호나 변의 번호가 잘못되었다.
• ERR 7: 다른 기술적인 문제가 발생했으므로 진행요원에게 도움을 요청하기 바란다.

채점

15개의 상자 각각에 대해 내부 구조를 최대한 상세하게 알아낸 결과를 텍스트 파일로 제출하면 이것이 채점 대상이 된다.

• 제출한 답안에서 ., /, \의 위치가 하나라도 틀린 게 있으면 그 답안의 전체 점수는 0점이 된다. 따라서 내부 구조를 확실히 알 수 없는 칸은 반드시 ?로 표기해야 한다.
• 그렇지 않은 경우, 수험자의 점수는 100×(정확한 내부 구조를 알아 낸 칸 수) / (0점 처리되지 않은 올바른 답안을 제출한 전체 수험자 중, 정확한 내부 구조를 가장 많이 알아 낸 칸 수)로 상대적으로 산정된다.

참고: 주최 측이 자체적으로 개발한 답안 프로그램은 어떤 블랙박스이든 그 내부 구조를 8분 이내의 시간에 100% 완벽하게 알아 낼 수 있다.