
제 19회는 2007년 8월 15일부터 22일까지 크로아티아 자그레브에서 열렸다. 05년과 마찬가지로 제출형 문제가 등장하지 않았으며, 부분점수가 전혀 없는 깔끔한 최적해 문제들이다. 대화형으로 위치를 찍어 알아 맞히는 문제를 "크로아티아 식" 체스판 무늬에다 접목한 1번은 외계인 소재까지 동원한 게 나름대로 재치까지 느껴진다.
04년부터 관례적으로 덧붙여지고 있는 '작은 테스트 케이스' 조건에 대한 배려(전체 테스트 케이스 중 몇 점은 N의 값이 매우 작다는 식)는 더욱 자상해졌다. 일부 문제는 경시 도중에도 공식 채점 시스템을 부분적으로 활용하여 작성 중인 프로그램을 "예비 채점"해 볼 수도 있게 수험자를 배려했다. (2, 4, 6번) 올해는 최초로 몇몇 문제에 "64비트 정수를 사용하여 출력하시오"란 단서가 붙은 것도 인상적이다. (3번과 5번)
600점 만점에 금메달 입상자의 최고 점수는 574점, 동메달 입상자의 최저 점수는 187점이었다. 우리나라는 은메달 2개, 동메달 2개를 획득해 예년보다 성적이 상대적으로 저조했다. 중국은 참가자 4명 전원이 금메달을 획득하고, 러시아도 금 3, 은 1이었다.
원문이 있는 곳: http://ioi2007.hsin.hr/index.php?page=tasks
미스터리 서클에 대해서 들어 보았는가? (넓은 밭을 공중에서 내려다봤을 때, 곡식의 일부만 누군가에 의해 기하학적인 의미를 띠는 형태로 연달아 짓눌려 있는 모습. 외계인의 소행인 것으로 추정됨) 미르코는 이 괴이한 무늬에 관심이 매우 많다.
그러던 어느 여름날 밤, 그는 할머니의 밭에 자기가 그런 서클을 직접 만들어 보기로 마음먹었다. 그는 국가에 대한 자부심이 남다른지라 모양도 크로아티아 전통 문장에 들어가 있는 체스판 무늬로 정했다. 13개의 붉은 칸과 12개의 흰 칸이 교차하는 5x5 크기의 체스판 모양 모늬이다.

할머니의 밭은 N×N개의 칸으로 구성된 정사각형 모양이다. 좌측 하단이 좌표상으로 (1, 1)이고 우측 상단이 (N, N)이다.
미르코는 실제 체스판 무늬에서 빨간색으로 칠해지는 부분에 해당하는 칸의 곡식만 짓눌러서 표가 나게 했다. 그 크기는 홀수 M≥3을 택해서 체스판의 한 정사각형은 밭에서 M×M만큼의 칸을 차지하게 설정했다. 물론 그렇게 그려진 5×5 크기의 체스판 전체(따라서 한 변의 길이는 5M)가 밭 안에 잘리는 영역 없이 모두 들어간다.
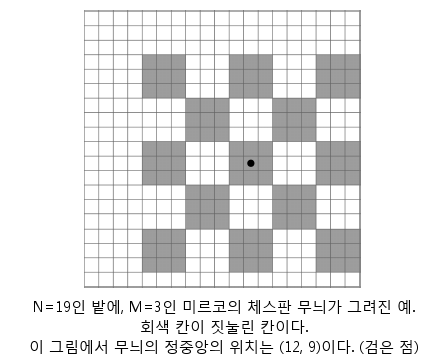
그렇게 밭에다 체스판 무늬 ‘미스터리 서클’을 만들어 놓은 뒤 미르코는 잠들었다. 그 사이에 이 무늬는 그의 바람대로 진짜 외계인들의 시선을 사로잡게 되었다. 그들은 밭 위를 고공 비행하면서 특수한 장비로 밭의 상태를 측정하기 시작했는데, 이 장비는 한 번에 밭의 한 칸의 상태만을 측정할 수 있다. (곡식이 짓눌렸는지의 여부)
외계인들은 약간의 노력 끝에 곡식이 짓눌려 있는 한 칸을 찾아냈다. 하지만 M의 값(체스판 정사각형 하나가 차지하는 크기)도 모르고 이 정보만으로는 아직 체스판 무늬의 형체를 파악하기에 매우 부족하다. 여러분은 외계인들이 미르코의 걸작품을 보면서 마음껏 감탄할 수 있도록 그들을 도와야 한다.
밭의 크기 N (15≤N≤2,000,000,000)과 곡식이 짓눌려 있는 시작점의 위치 (X0, Y0)를 입력 받고, 외계인의 특수 장비를 동원하여 이 밭에 있는 미르코의 체스판 무늬의 정중앙을 찾는 프로그램을 작성하시오. 한 테스트 케이스에 대해서 위치 쿼리는 최대 300번까지 할 수 있다.
이 문제는 대화형이다. 표준 출력 스트림을 통해 외계인 장비에다 명령을 보내고, 표준 입력 스트림을 통해 그 장비로부터 응답을 얻으면 된다.
채점 프로그램과 원활히 의사 소통하기 위해서는 문자열을 출력한 뒤에 언제나 표준 출력 스트림을 flush해 주어야 한다. 함께 제공되는 예제 코드에 언어별로 구체적인 요령이 나와 있다. 이 코드는 채점 시스템과 의사 소통하는 예만을 보여줄 뿐 정확한 답을 구하는 답안 프로그램이 아님을 유의하기 바란다.
모든 테스트 케이스는 수험자의 답안 프로그램이 어떤 형태로 쿼리를 하든 상관없이 유일한 정답을 구할 수 있는 형태이다. 또한, 테스트 케이스 중 전체의 40점에 해당하는 케이스는 체스판 정사각형의 크기 M이 100보다 작다.
다음은 앞의 그림과 같은 설정에서 답안 프로그램이 입출력을 주고 받으며 답을 구해 가는 과정을 나타낸 것이다.
| 출력 (명령) | 입력 (응답) |
| 19 7 4 | |
| examine 11 2 | true |
| examine 2 5 | false |
| examine 9 14 | false |
| examine 18 3 | true |
| solution 12 9 |
대회 진행 중에 수험자가 자신의 답안 프로그램을 테스트하는 방법은 세 가지가 있다.
가장 간단한 방법은 프로그램이 전적으로 표준 입출력에 의존하는 만큼, 키보드로 수험자가 직접 외계인의 장비를 가정하여 프로그램에 정보를 공급하는 것이다.
둘째는 외계인의 장비를 흉내내는 프로그램을 별도로 작성하는 것이다. 답안 프로그램과 그 장비 프로그램을 상호 연결해 주는 "connect"라는 유틸리티가 주최측 시스템에서 제공되고 있으므로 이를 활용하면 된다. 프로그램을 실행할 때 "./connect ./답안프로그램명 ./장비프로그램명" 식으로 명령을 내리도록 한다. 그 이후의 매개변수들은 모두 장비 프로그램에 그대로 전달된다.
셋째는 채점 시스템에 있는 TEST 기능을 이용하여, 채점 시스템이 수험자가 설정해 놓은 정답(지정된 M 값과 지정된 정중앙 위치)을 가정하여 답안 프로그램의 쿼리에 응답하게 하는 것이다. 단, 이 기능은 밭의 크기 N을 최대 100까지로만 설정할 수 있다.
테스트 케이스에는 세 줄이 있어야 한다.
채점 시스템은 답안 프로그램과 입출력을 주고받은 결과를 상세한 로그 파일로 알려줄 뿐만 아니라 아래의 상황처럼 테스트 케이스 자체에 잘못이 있을 때에도 에러 메시지를 출력해 준다.
다음은 앞의 그림과 같은 설정을 테스트 케이스로 나타낸 예이다.
19 3
7 4
12 9
지난 1964년에는 기록적인 대홍수가 자그레브 시가지를 강타했었다. 이때 건물이 많이 파괴되었는데, 이는 물의 하중으로 인해 건물을 이루는 벽이 붕괴했기 때문이다. 이번 문제에서는 그런 도시 형태를 단순하게 모델화한 정보가 입력으로 들어온다. 여러분은 이를 토대로 어떤 벽이 홍수 후에도 붕괴 없이 존속할 것인지를 찾아야 한다.
이 모델은 좌표평면 상에서 N개의 점과 W개의 벽으로 표현된다. 벽은 그 N개의 점 중 둘을 연결한 선의 형태로 존재하는데, 그 선은 중간에 다른 점을 관통하지 않으며 다른 선과 겹치거나 교차하지도 않는다. 단지 선의 끝점만이 서로 겹칠 수 있다. 또한 선은 좌표평면 상에서 수평선이나 수직선으로만 존재한다.
모델의 초기 상태는 비가 오기 전으로 모든 평면이 육지이다. 그러다 0이라는 시각에 홍수가 시작되어, 벽으로 사방이 둘러싸이지 않은 모든 외곽이 물로 뒤덮인다. 그로부터 정확히 1시간 후에는 물과 육지의 양면 경계를 이루고 있던 벽이 수압을 견디지 못하고 모두 무너진다. 벽이 무너짐으로써 경계가 없어진 곳에는 이내 물이 더 깊숙이 들어오고, 무너진 벽의 내부에 있던 다른 벽이 육지와 물의 경계가 된다. 이 벽도 역시 1시간이 더 지나면 무너질 것이다. 이 과정이 되풀이됨으로써 결국 무너질 벽은 다 무너지고 모든 영역에 물이 차게 된다.
다음은 지금까지 설명한 도시 모델의 한 예를 묘사한 것이다.
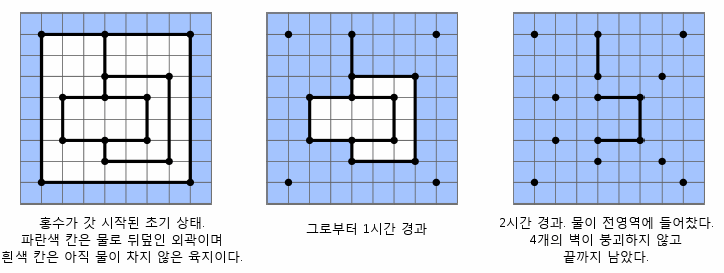
N개의 점의 좌표와 이들 점을 연결하는 W개의 벽에 대한 정보를 입력 받아, 이들 중 홍수 후에도 무너지지 않고 남아 있는 벽이 무엇인지 찾는 프로그램을 작성하시오.
첫째 줄에는 정수 N (2≤N≤100,000)의 값이 들어있다. 좌표평면에 있는 점의 개수이다. 다음 N개의 줄에는 1부터 N째까지 각 점의 X, Y 좌표가 하나씩 들어있다. 범위는 0 이상 1,000,000 이하이다. 점들의 위치는 모두 다르며, 두 점이 같은 지점에 겹치는 경우는 없다.
다음 줄에는 벽의 개수 W (1≤W≤2N)의 값이 들어있다. 그리고 다음 W개의 줄에는 서로 다른 정수 A, B (1≤A≤N, 1≤B≤N)가 있으며 이는 초기 상태에 이 모델에 A째 점과 B째 점을 연결하는 벽이 존재함을 나타낸다. 벽 역시 1부터 W까지 읽는 순서대로 서열을 매기면 된다.
15
1 1
8 1
4 2
7 2
2 3
4 3
6 3
2 5
4 5
6 5
4 6
7 6
1 8
4 8
8 8
17
1 2
2 15
15 14
14 13
13 1
14 11
11 12
12 4
4 3
3 6
6 5
5 8
8 9
9 11
9 10
10 7
7 6
첫째 줄에는 홍수 후에도 남아 있는 벽의 개수 K를 출력한다. 그리고 다음 K개의 줄에는 그 벽의 서열 번호를 한 줄에 하나씩 출력한다. 아무 순서로나 출력해도 무방하다. (메모리 제한: 32MB, 시간 제한: 2초)
4
6
15
16
17
테스트 케이스 중 전체의 40점에 해당하는 케이스는 좌표의 최대 범위가 500이다. (1백만보다 훨씬 작은) 그리고 위의 케이스뿐만 아니라 나머지 15점에 해당하는 추가 케이스는(총 55점) 점 N의 최대 개수가 500이다.
프로그램 작성의 편의를 도모하기 위해, 이 문제는 대회 진행 중에 부분적으로 예비 채점이 가능하다. 수험자는 작성하고 있는 프로그램을 최대 10번까지 제출해서 정식 채점 때 쓰이는 테스트 케이스의 일부에 대한 채점 결과를 통지 받을 수 있다.
새로운 해적선이 건조 중이다. 배에는 길이가 다른 N개의 돛대가 있다. 각 돛대는 단위 길이에 해당하는 마디로 나뉘며 돛대의 높이는 언제나 그 단위 길이의 배수이다. 돛대에 꽂히는 돛은 균일한 크기로서 그 높이가 단위 길이와 일치하고, 정확하게 돛대의 각 마디에 꼭 맞게만 장착된다. 돛은 그런 식으로 돛대의 아무 마디에나 고르게 장착할 수 있지만 돛대의 마디 하나에는 돛을 최대 하나만 달 수 있다.
배는 뒤에서 불어오는 바람을 받고 앞으로 밀려 나아가는데, 같은 바람을 받아도 돛을 어떻게 다냐에 따라 배가 받는 동력이 달라진다. 진행 방향을 기준으로 앞쪽에 있는 돛은 같은 높이에 있는 뒤쪽 돛에 가려서 바람을 뒤쪽보다 덜 받게 되고, 그만큼 돛으로서의 역할을 제대로 못 하게 된다.
이에 우리는 각 돛에 대해 ‘비효율 지수’라는 개념을 정의하기로 한다. 그 돛과 높이가 같으면서 뒤에 있는 돛의 개수를 말한다. 또한 배의 ‘전체 비효율 지수’란, 그 배의 모든 돛의 비효율 지수의 합을 일컫는다.
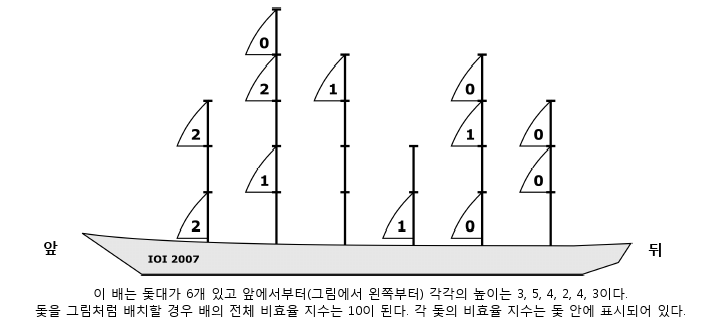
배에 세우고자 하는 돛대의 개수와 각각의 높이, 그리고 각 돛대마다 달고자 하는 돛의 개수를 입력 받아서 그 배가 구조적으로 가질 수 있는 최소 ‘전체 비효율 지수’를 계산하는 프로그램을 작성하시오.
첫째 줄에는 돛대의 개수 N (2≤N≤100,000)의 값이 들어있다. 그리고 다음 N개의 줄에는 정수 H와 K (1≤H≤100,000; 1≤K≤H)가 있는데 각각 돛대의 높이와 그 돛대에 장착되는 돛의 개수이다. 돛대에 대한 정보는 진행 방향을 기준으로 앞에서 뒤로 가는 순서로 나와 있다.
6
3 2
5 3
4 1
2 1
4 3
3 2
이 배의 최소 전체 비효율 지수 하나만을 출력하면 된다. (메모리 제한: 64MB, 시간 제한: 1초)
10
주의: 64비트 정수를 사용하도록 한다. (C/C++에서는 long long, 파스칼에서는 int64)
테스트 케이스 중 전체의 25점에 해당하는 케이스는 돛을 돛대에 배치하는 조합 가짓수가 1백만 가지 이하이다.
석탄을 캐는 광산이 두 군데 있고, 각 광산에는 광부들이 작업을 하고 있다. 채굴 작업은 고된 일이기 때문에 광부에게는 음식을 통한 지속적인 영양 섭취가 필요하다. 매 시각마다 한 음식 세트가 도착하고 이를 공급 받은 광부들은 일정량의 석탄을 생산해 낸다. 음식 세트에는 고기, 생선, 빵 이렇게 세 종류가 있다.
광부들은 다양한 메뉴로 식사를 하고 싶어하기 때문에 끼니마다 음식 세트가 제각각일수록 작업 생산성이 올라간다. 이를 구체적으로 표현하면 이렇다. 음식 세트가 하나 도착하면 이를 먹고 광부들이 작업을 해서 석탄을 생산하는데, 그 생산량은 지금 먹은 음식 세트와 그 전과 그 전전에 먹은 음식 세트(만약 그런 적이 있다면) 이렇게 최대 세 세트를 비교했을 때,
매 시각마다 앞으로 어떤 음식 세트가 순서대로 공급될 것인지 스케줄이 나와 있다. 그 순서 자체를 바꿀 수는 없지만 어떤 음식을 두 광산 중 어디에 보낼지를 적절히 조절함으로써 광부들에게 최대한 균형 잡힌 식단을 제공할 수 있고, 이것이 광산 채굴 효율을 극대화할 수 있다. 음식 세트 하나를 둘로 나눌 수는 없으며 어차피 같은 시간엔 음식을 받은 한 광산에서만 작업이 진행된다.
두 광산에 균형 잡힌 횟수나 간격으로 음식을 공급해야 할 필요는 없다. 한 광산을 한참 동안 놀리고 있어도 되고, 아예 한 곳에다가만 공급을 올인해도 괜찮다. 오로지 특정 광산에 음식을 공급할 때, 예전과 비교해서 메뉴의 다양성만 보장되면 된다.
광산에 공급되는 음식 세트 리스트를 입력 받아, 이를 두 광산에 적당한 순서로 보냈을 때 캘 수 있는 석탄의 최대량을 계산하는 프로그램을 작성하시오.
첫째 줄에는 음식 세트의 총 개수 N (1≤N≤100,000)의 값이 들어있다. 그리고 둘째 줄에는 시간 순으로 공급되는 음식 세트를 의미하는 문자열이 N 글자 들어있다. 문자는 대문자로 M(고기), F(생선), B(빵) 이렇게 셋 중 하나이다.
| #1 | #2 |
6 |
16 |
이 공급 하에서 가능한 석탄의 최대 채굴량을 정수 하나로 출력한다. (메모리 제한: 16MB, 시간 제한: 1.5초)
| #1 | #2 |
12 |
29 |
입력 예제 #1을 살펴보자(M1B2M3F4F5B6). 음식 세트를 각각 1, 1, 2, 2, 1, 2번 광산의 순으로 보낼 경우 1번 광산에는 M1B2F5, 2번 광산에는 M3F4B6가 공급되어 두 광산에 모두 서로 다른 식사가 제공되고 따라서 채굴량도 1, 2, 3의 순으로 올라간다. 그래서 최대 채굴량은 1+2+3과 1+2+3의 합인 12가 된다. 물론 1, 2, 2, 2, 1, 1 같은 다른 순서로도 최대 채굴량을 달성할 수 있다.
테스트 케이스 중 전체의 45점에 해당하는 케이스는 N의 값이 최대 20이다.
프로그램 작성의 편의를 도모하기 위해, 이 문제는 대회 진행 중에 부분적으로 예비 채점이 가능하다. 수험자는 작성하고 있는 프로그램을 최대 10번까지 제출해서 정식 채점 때 쓰이는 테스트 케이스의 일부에 대한 채점 결과를 통지 받을 수 있다.
미르코와 슬라브코는 동물 모양의 장난감을 갖고 놀고 있다. 노는 방법은 다음과 같다. 먼저 아래 그림과 같은 세 개의 게임판(1~3차원 칸으로 된 균일 간격 격자) 중 하나를 고른다. 그리고 게임판 내부 임의의 칸(그림에서 동그라미로 표현된)에 N개의 동물 장난감을 집어넣는다.
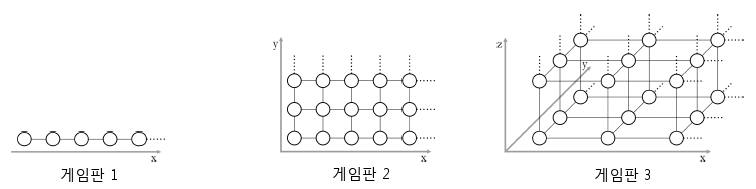
그림에서 보다시피 어떤 칸에서 인접한 칸은 각 차원의 축과 평행한 선분으로만 연결되어 있는데, 두 칸의 ‘거리’는 다른 칸으로 가기 위해 거쳐야 하는 선분의 최소 개수로 정의된다. 다시 말해 3차원을 예로 들 때 임의의 위치에 있는 칸 A(x1, y1, z1)와 B(x2, y2, z2)의 거리는 단순히 |x1-x2|+|y1-y2|+|z1-z2|가 되며, 2차원이나 1차원의 경우도 같은 계산법이 성립한다는 뜻이다.
게임판에서 서로 거리가 D 이하인 칸에 있는 두 동물은 울음소리를 통해 상대방을 알아차릴 수 있다. 슬라브코는 이렇게 서로 알아차릴 수 있는 동물의 쌍이 얼마나 되는지 알고 싶어한다.
게임판의 종류, 그 게임판에 있는 모든 동물들의 위치와 최장 가청 거리 D 값을 입력 받아 서로 충분히 가까이 있는 동물의 쌍이 얼마나 있는지 찾는 프로그램을 작성하시오.
첫째 줄에는 네 개의 정수가 들어있으며 의미는 순서대로 다음과 같다.
B=1일 때는 M은 최대 75,000,000이며 B=2일 때는 최대 75,000이다. B=3일 때는 최대 75이다.
다음 N개의 줄에는 각 줄마다 동물의 위치 좌표를 나타내는 정수가 B개 들어있다. 정수의 범위는 1 이상 M 이하이다. 한 칸에 두 마리 이상의 동물이 겹쳐 있을 수도 있다.
| #1 | #2 | #3 |
1 6 5 100 |
2 5 4 10 |
3 8 10 20 |
최장 가청 거리 이내에 있는 동물의 쌍수를 출력한다. (메모리 제한: 150MB, 시간 제한: 4초)
주의: 64비트 정수를 사용하도록 한다. (C/C++에서는 long long, 파스칼에서는 int64)
| #1 | #2 | #3 |
4 |
8 |
12 |
입력 예제 #1(1차원) 살펴보면, 위에서부터 1번과 5번 동물(25, 20), 1번과 6번(25, 23), 2번과 3번(50, 50), 5번과 6번(20, 23) 동물의 거리가 최장 가청 거리인 5 이하이다. 이렇게 총 4쌍이다.
#2 (2차원)는 1번과 2번(거리 2+0=2), 1번과 4번(1+3=4), 1번과 5번(1+2=3), 2번과 3번(1+2=3), 2번과 4번(1+3=4), 3번과 4번(2+1=3), 3번과 5번(4+0=4), 4번과 5번(2+1=3) 이렇게 총 8쌍이다.
테스트 케이스 중 전체의 30점에 해당하는 케이스는 N의 값이 최대 1000이다. 그리고 1, 2, 3차원 중 단 한 경우에 대해서라도 완벽하게 문제를 풀면 최소한 30점 이상을 받을 수 있다.
미르코와 슬라브코는 크로아티아에서 해마다 열리는 2인승 사이클 장거리 경주의 참가를 앞두고 열심히 기량을 쌓고 있다. 그들은 연습 코스를 설정해 놓고 그 코스대로 꾸준히 주행 연습을 하고 싶어한다.
주변에는 N개의 도시와 M개의 길이 있다. 길은 두 도시를 연결하며 어느 방향으로나 주행이 가능하다. M개의 길 중 정확하게 N-1개는 포장된 도로이며, 나머지는 비포장 오솔길이다. 단, 모든 도시는 포장 도로만으로도 상호 왕래가 가능하게 연결돼 있다. 다시 말해 N개의 도시와 N-1개의 포장 도로는 트리 구조를 형성한다는 뜻이다.
아울러, 한 도시를 관통하는 길(포장, 비포장 막론)의 최대 개수는 10개이다.
연습 코스는 한 도시에서 시작해서 임의의 길을 따라 운행한 뒤, 다시 그 도시로 돌아오는 형태이다. 미르코와 슬라브코는 늘 새로운 길을 가는 것을 좋아하기 때문에, 전에 지나쳤던 도시를 또 들르거나 전에 주행했던 도로를 다시 주행하는 일이 없도록 코스를 만들고 싶어한다. 코스는 아무 도시에서나 시작해도 되며, 모든 도시를 다 거쳐야 할 필요는 없다.
2인승 자전거는 뒤에 타는 게 체력 소모가 더 적다. 앞 사람이 역풍을 가려 주기 때문이다. 그래서 둘은 새로운 도시에 도착할 때마다 자리를 교대한다. 이런 상황에서 두 사람이 서로 동일한 양만치 훈련을 하기 위해서는 연습 코스는 짝수 개의 길을 경유하도록 정해야 한다.
그런데 미르코와 슬라브코를 시샘하는 경쟁자들은, 길의 일부를 폐쇄함으로써 그 두 사람이 위에서 언급한 모든 조건을 만족하는 연습 코스를 전혀 찾을 수 없게 만들기로 작정했다. 비포장길은 폐쇄하는데 제각기 비용이 들며, 그 비용은 양의 정수로 표현된다. 다만 포장 도로는 폐쇄가 불가능하다.
도시와 도로망에 대한 정보를 입력 받아, 위에서 언급한 모든 조건을 만족하는 사이클 연습 코스가 존재하지 않게 만드는데 필요한 최소한의 도로 폐쇄 비용을 계산하는 프로그램을 작성하시오.
첫째 줄에는 도시의 개수 N과 길의 개수 M이 있다. (2≤N≤1000, N-1≤M≤5000) 그리고 다음 M개의 줄에는 길의 정보를 나타내는 정수 A, B, C가 있다. (1≤A≤N, 1≤B≤N, 0≤C≤10,000) 도시 A와 도시 B가 길로 연결되어 있으며, 이 길의 폐쇄 비용이 C임을 의미한다. 단, C가 0이면 이 길은 폐쇄할 수 없는 포장 도로라는 뜻이다.
그래프 상으로 한 도시 정점에 붙을 수 있는 도로 선분의 최대 개수는 앞서 말했듯이 10이다. 임의의 두 도시를 연결하는 도로는 최대 하나밖에 존재하지 않는다. (당연한 말임. 즉, 한 직통 도로가 막혔다고 해서 다른 직통 도로를 이용하면 되는 상황까지 고려하지는 않아도 된다는 뜻.)
| #1 | #2 |
5 8 |
9 14 |
문제 조건을 충족하기 위해 막아야 하는 길들의 폐쇄 비용의 합을 정수로 출력하면 된다. (메모리 제한: 64MB, 시간 제한: 0.3초)
| #1 | #2 |
5 |
48 |
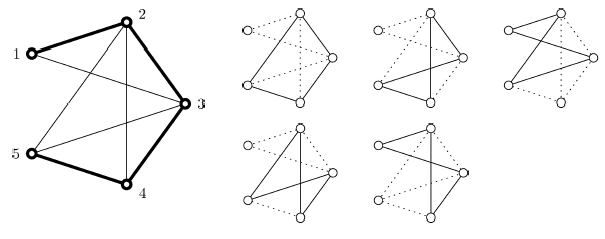
위의 그림은 입력 예제 #1을 실제 그래프로 표현한 것이다. 굵은 선은 포장 도로를 의미한다. 이때 미르코와 슬라브코의 조건을 만족하는 연습 코스는 오른쪽과 같이 다섯 가지가 존재하는데, 도로 1-3, 3-5, 2-5를 폐쇄해서 제거하면 다섯 가지 경로 중 어느 것도 제 구실을 못 하게 된다. 세 도로를 폐쇄하는 비용은 2+2+1=5이다.
물론 도로 2-4와 2-5 이렇게 둘만 막아도 목표를 달성할 수는 있지만 이 경우 비용은 6으로 더 커지게 된다.
테스트 케이스 중 전체의 30점에 해당하는 케이스는 예제 #1처럼 포장 도로가 도시와 도시를 일렬로 쭉 연결하고 있다. 즉, 한 도시에서 세 개 이상의 포장 도로가 만나지 않는다는 뜻이다.
프로그램 작성의 편의를 도모하기 위해, 이 문제는 대회 진행 중에 부분적으로 예비 채점이 가능하다. 수험자는 작성하고 있는 프로그램을 최대 10번까지 제출해서 정식 채점 때 쓰이는 테스트 케이스의 일부에 대한 채점 결과를 통지 받을 수 있다.