제 6회는 1994년 7월 3일부터 10일까지 스웨덴 하닝거에서 열렸다. 난이도가 매우 높아지고, 형식으로나 내용으로나 현재와 같은 IOI 문제 양식의 틀과 대회 규정이 이 대회 때 완전히 잡혔다. 문제의 조건 역시 매우 논리적으로 잘 설계되었다. 486 33MHz를 기준으로 각 답안 프로그램이 답을 구하는 제한 시간은 3번 소수 만들기만 90초이고 나머지는 모두 30초이다.
원문이 있는 곳: http://olympiads.win.tue.nl/ioi/ioi94/contest/index.html
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
위 그림은 크기가 5인 숫자 삼각형의 한 모습이다.
맨 위층 7부터 시작해서 아래에 있는 수 중 하나를 선택하여 아래층으로 내려올 때, 이제까지 선택된 수의 합이 최대가 되는 경로를 구하는 프로그램을 작성하라. 아래층에 있는 수는 현재 층에서 선택된 수의 대각선 왼쪽 또는 대각선 오른쪽에 있는 것 중에서만 선택할 수 있다.
삼각형의 크기는 1 이상 100 이하이다. 삼각형을 이루고 있는 각 숫자는 모두 정수이며, 범위는 0 이상 99 이하이다.
INPUT.TXT의 첫 줄에는 삼각형의 크기가, 다음 줄부터는 삼각형에 들어갈 수들이 위층부터 들어있다. 위의 예라면 INPUT.TXT는 아래와 같다.
5 7 3 8 8 1 0 2 7 4 4 4 5 2 6 5
합이 가장 큰 경로대로 수를 선택했을 때의 합을 OUTPUT.TXT에 출력한다. 위의 예라면 7-3-8-7-5를 선택했을 때의 합인 30을 출력하면 된다.

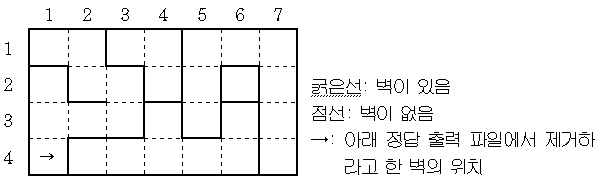
위의 그림은 어떤 성의 내부를 나타낸 지도이다. 지도를 읽어 다음을 계산하는 프로그램을 작성하라.
성은 m×n(m, n은 최대 50까지의 값을 갖는다.)개의 정사각형 칸으로 나뉘어지며, 한 칸 주위에는 최소 0개, 최대 사방 모두로 4개의 벽이 있다.
성 지도의 정보는 INPUT.TXT에 칸 단위로 저장되어 있다.
파일 처음에는 세로 칸의 개수, 가로 칸의 개수가 들어있고, 다음부터는 칸을 둘러싸고 있는 벽의 정보가 수치로 들어있다. 배열된 정보 역시 세로, 가로의 순이며, 수치는 0부터 15까지의 값으로, 1(왼쪽에 벽이 있다), 2(북쪽에 벽이 있다), 4(오른쪽에 벽이 있다), 8(남쪽에 벽이 있다)의 합이다.
그러므로 두 칸 사이에 있는 벽의 정보는 겹쳐서 들어있게 된다. 가로 1, 세로 1 위치의 남쪽 벽 정보는 가로 1, 세로 2 위치의 북쪽 벽 정보와 일치한다.
성에는 언제나 적어도 두 개 이상의 방이 있다. 위에 나온 지도를 INPUT.TXT로 나타내면 아래와 같다.
4 7 11 6 11 6 3 10 6 7 9 6 13 5 15 5 1 10 12 7 13 7 5 13 11 10 8 10 12 13
OUTPUT.TXT 파일에는 다음 정보가 세 줄에 걸쳐 기록한다. 먼저 방의 개수, 가장 넓은 방의 넓이(차지하는 칸 수), 다음에는 제거할 벽이 있는 칸의 위치를 세로 좌표부터 기록하고 다음에 그 벽이 방향을 기록한다.
위의 예에 대한 출력 결과는 아래와 같다. (4 1 E말고 다른 최적해가 여러 개 있을 수 있으나, 그중하나만 구하면 된다.)
5 9 4 1 E
| 1 | 1 | 3 | 5 | 1 |
| 3 | 3 | 2 | 0 | 3 |
| 3 | 0 | 3 | 2 | 3 |
| 1 | 4 | 0 | 3 | 3 |
| 3 | 3 | 3 | 1 | 1 |
위 그림은 소수 정사각형의 모습이다. 각각의 행, 열, 두 대각선 방향으로는 다섯 자리의 소수가 적혀 있다. 가로와 대각선 방향으로 배열된 수는 왼쪽에서 오른쪽으로 읽는다. 세로로 배열된 수는 위에서 아래로 읽는다. INPUT.TXT에 있는 데이터를 읽어, 이러한 소수 정사각형을 만드는 프로그램을 작성하라.
소수 12개는 모두 자릿수의 합이 같아야 한다. (위는 11인 경우이다.)
좌측 상단 칸에 있는 숫자는 미리 정해진다. (위는 1인 경우이다.) 같은 소수가 여러 개 들어있을 수도 있다. 조건을 만족하는 해가 여러 개 있다면 모두 출력해야 한다.
다섯 자리의 소수는 0으로 시작해서는 안 된다. 즉 00003은 다섯 자리의 소수가 아니다.
답안 프로그램은 INPUT.TXT에서 데이터를 읽는다.
처음에는 소수의 자릿수의 합이 들어있고 다음 줄에는 좌측 상단에 있는 미리 정해진 숫자가 들어있다. 파일은 이렇게 두 줄이다. 또한 지정한 조건을 만족하는 해가 반드시 있다고 가정한다. 위의 경우 입력 파일은 아래와 같다.
11 1
OUTPUT.TXT에 결과를 출력하며, 찾은 해인 소수 정사각형을 한 줄에 하나씩 걸쳐 총 다섯 줄로 기록한다. 위의 예에서는 3개의 해가 있다. 이와 같은 경우 OUTPUT.TXT에 수록돼 있어야 하는 정사각형은 아래와 같다. (답 사이에 빈줄은 붙이든 말든 상관없다.)
11351 14033 30323 53201 13313 11351 33203 30323 14033 33311 13313 13043 32303 50231 13331
|-------| |-------| |-------|
| | | | | | |
|---O | |---O | | O |
| | | | | |
|-------| |-------| |-------|
A B C
|-------| |-------| |-------|
| | | | | |
| O | | O | | O |
| | | | | | | | |
|-------| |-------| |-------|
D E F
|-------| |-------| |-------|
| | | | | |
| O | | O---| | O |
| | | | | | | |
|-------| |-------| |-------|
G H I
위 그림에서 보는 바와 같이 3×3 배열에 9개의 시계가 있다. 이 문제의 목표는 최소한의 동작으로 모든 시계의 바늘을 12시로 맞추는 것이다.
시계 바늘을 돌리는 방법은 9가지가 있다. 이 방법을 동작이라고 하겠다. 한 동작이 선택되면 그 동작에 해당하는 시계 바늘을 시계 방향으로 90도 돌린다. 각 동작에 반응하는 시계 번호는 다음과 같다.
INPUT.TXT에서 9개의 숫자를 읽어들인다. 이 숫자는 시계의 현재 상태를 나타내며, 다음과 같다: 0=12시, 1=3시, 2=6시, 3=9시
위의 예를 INPUT.TXT로 나타내면 다음과 같다.
3 3 0 2 2 2 2 1 2
OUTPUT.TXT에 모든 시계를 12시로 돌려놓는 가장 짧은 동작 순서를 출력한다. 최적해가 여러 개 있어도 하나만 출력하면 된다. 위의 예인 경우 OUTPUT.TXT파일 내용은 다음과 같으면 된다.
5849
각각의 숫자는 현재 시계 바늘이 몇 시를 가리키고 있는지를 나타낸다. 0 = 12시, 1 = 3시, 2 = 6시, 3 = 9시이다.
3 3 0 3 0 0 3 0 0 0 0 0 0 0 0 2 2 2 5 → 3 3 3 8 → 3 3 3 4 → 0 3 3 9 → 0 0 0 2 1 2 2 2 2 3 3 3 0 3 3 0 0 0
어떤 사람이 버스 정거장에 12시에 도착한다. 그리고 12시부터 12시 59분까지 거기 있는다. 노선이 다른 여러 버스들이 이 정거장에 선다. 그는 버스가 도착하는 시각을 주의 깊게 관찰하고 있는다.
노선이 같은 버스는 12시 정각부터 59분까지 같은 시간 간격으로 규칙성 있게 도착한다. 버스를 관찰한 시간은 0부터 59분까지이다. 각 노선을 달리는 버스는 그 동안 적어도 두 번은 정거장에 선다.
노선이 다르더라도 어떤 버스 노선의 시간 스케줄은 최초 도착 시간이나 시간 간격 중 하나 이상이 다른 노선의 스케줄과 일치할 수 있다. 그런 이유로, 같은 시각에 노선이 다른 버스가 두 대 이상 도착하면 그 시각은 온 버스 수만큼 중복 기록한다. 즉, 만약 최초 도착 시간과 오는 간격이 완전히 같은 두 노선이 있더라도 그 노선을 다니는 버스들이 온 시각은 구분되어 따로 입력 파일에 기록된다는 뜻이다.
버스가 도착한 시간 기록을 읽어들여 이 간격대로 있을 수 있는 서로 다른 버스 노선들을 구해 이들의 시간 스케줄을 출력하는 프로그램을 작성하라. 그리고 찾아낸 버스 노선마다 그 노선의 첫 도착 시간과 다음 간격을 출력하라. 물론 버스 노선이 가장 적은 경우를 찾아야 할 것이다.
입력 파일인 INPUT.TXT에는 버스가 선 횟수인 n이 가장 먼저 들어오고(n<=300) 다음부터 버스가 온 시간이(0~59) 오름차순으로 들어 있다. 예를 들면
17 0 3 5 13 13 15 21 26 27 29 37 39 39 45 51 52 53
OUTPUT.TXT에는 버스 노선의 첫 도착 시각과 다음 간격을 한 줄씩 기록한다. 순서는 따질 필요 없다. 최적해가 여러 개 있더라도 하나만 출력하면 된다. 위의 경우 출력 결과는 다음과 같다. 올바른 정답이 나왔다고 전제할 때, 서로 다른 버스 노선의 개수는 최대 17개까지 있을 수 있다. 위 예제에서 기록된 시각을 보면 노선이 최소한 세 개 있었다고 생각할 수 있다.
0 13 ← 0 . . 13 . . 26 . . . 39 . . 52 . (5번) 3 12 ← . 3 . . 15 . . 27 . . 39 . 51 . . (5번) 5 8 ← . . 5 13 . 21 . . 29 37 . 45 . . 53 (7번)
부채꼴로 나누어진 원이 하나 있다. 또한 n(n<=6), m(m<=20), k(k<=20) 세 양수가 있다. n은 부채꼴의 개수이다. 다음 각각의 부채꼴 안에 넣을 정수를 고른다. 들어가는 모든 정수는 k 이상이어야 한다. 모든 부채꼴에 수가 들어가면 여러분은 부채꼴에 있는 수를 하나 뽑거나 서로 인접한 둘 이상의 부채꼴에 있는 수들을 더해서 새로운 수를 만들 수 있다. 이런 방법을 이용해서 여러분은 m부터 i사이의 모든 정수를 빠짐없이 만들어낼 수 있을 것이다. (m, m+1, m+2, ..., i)
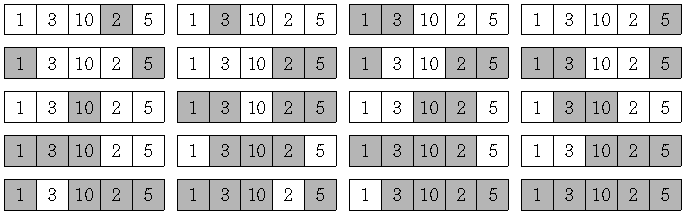
이번 문제는 n, m, k가 제시됐을 때, 위와 같은 방법을 써서 i값을 가장 크게 하려면 부채꼴 안에 어떤 수를 넣어야 하는지를 구하는 것이다. 아래에 n=5, m=2, k=1일 때 2부터 이 때 i의 최대값인 21까지의 수를 조합하여 만든 모습이 실려 있다.
INPUT.TXT에는 n, m, k값을 의미하는 세 개의 정수가 있다. 한 예는 아래와 같다.
5 2 1
출력 파일인 OUTPUT.TXT에는 다음과 같은 내용이 있어야 한다.
단, 부채꼴의 수열은 가장 작은 수부터 시작해야 한다. 그래서 (2 10 3 1 5)는 가장 작은 수로 시작하지 않았기 때문에 답이 아니다. 한편, 순서가 바뀐 것도 다른 답으로 인정하기 때문에 (1 3 10 2 5)와 (1 5 2 10 3)은 모두 포함돼야 한다. 마찬가지로 답이 (1 1 2 3), (1 3 2 1), (1 2 3 1), (1 1 3 2)와 같이 있는 경우도 다 출력해야 한다.
위의 예제 입력 파일에 대한 출력은 다음과 같다.
21 1 3 10 2 5 1 5 2 10 3 2 4 9 3 5 2 5 3 9 4
다음은 부채꼴에 (1 3 10 2 5)가 있을 때, 이 수들을 조합하여 2부터 21까지의 수를 만든 모습이다. 처음과 끝이 이어져 있다고 생각하고 살펴보기 바란다.