제 8회

제 8회는 1996년 7월 25일부터 8월 1일까지 헝가리 베스프햄에서 열렸다. 난이도는 7회와 비슷한 것 같다. 200점 만점에 금메달 입상자의 최고 점수는 196점, 동메달 입상자의 최저 점수가 103점이었으나, 각 문제의 자세한 채점 방식은 공식 홈페이지에 나와 있지 않다.

원문이 있는 곳: http://olympiads.win.tue.nl/ioi/ioi96/contest/index.html

1. 숫자 게임

2. 생산 공정의 처리

1. 숫자 게임

둘이서 하는 다음 게임을 하나 생각해 보자. 게임판은 자연수로 된 1차원 수열이다. 이 게임은 두 사람이 번갈아 가며 하며, 자기 차례가 된 사람은 그 수열의 왼쪽 끝이나 오른쪽 끝에 있는 수를 하나 선택한다. 선택된 수는 수열에서 지워진다. 이런 과정을 되풀이하여 모든 수가 지워지면 게임이 끝나고, 이제까지 자신이 선택한 수의 합이 더 많은 사람이 이긴다. 합이 두 명 다 같으면 먼저 한 사람이 이긴 것으로 한다. 나중에 하는 사람도 최선을 다해서 게임을 한다. 첫째 선수가 게임을 먼저 시작한다.

처음에 숫자가 짝수 개 있으면, 게임을 먼저 한 사람이 반드시 이기는 방법이 존재한다. 이번 문제는 첫째 선수가 게임에서 반드시 이기는 전략을 구현하는 프로그램을 작성하는 것이다. 둘째 선수는 제공되는 라이브러리가 맡아 한다. 그래서 답안 프로그램과 라이브러리는 StartGame, MyMove와 YourMove라는 세 가지 함수로 서로 대화하며 게임을 한다. 첫째 선수는 인자가 없는 StartGame 함수를 먼저 호출하여 게임을 초기화해야 한다. 그런 다음 자기 차례 때 게임판의 왼쪽 끝에 있는 수를 선택하려고 한다면 MyMove('L')이라는 함수를 호출한다. 비슷하게 오른쪽 끝을 선택하려면 'R'이라는 인자를 주면 된다. 이 함수가 실행되면 상대방인 컴퓨터는 자기도 바로 수를 둔다. 컴퓨터가 어디를 선택했는지를 알려면 YourMove(C)라는 함수를 호출한다. C는 문자형이며, 호출 뒤 C에 컴퓨터가 선택한 수열의 방향을 나타내는 'L' 또는 'R'값이 들어간다. (C/C++에서는 YourMove(&C)와 같은 형식으로 호출한다.)

입력 자료

INPUT.TXT의 첫 줄에는 처음에 게임판에 있는 숫자들의 개수 N이 들어있다. N은 2 N 100인 짝수이다. 다음 N줄에는 게임 초기에 게임판의 왼쪽부터 들어갈 수들이 있다. 각 수의 최대값은 200이다.

출력 자료

게임이 끝나면 답안 프로그램은 최종 결과를 OUTPUT.TXT에 기록해야 한다. 파일에는 첫 줄에 두 개의 숫자가 들어있다. 앞의 수는 답안 프로그램이, 뒤의 수는 컴퓨터가 선택한 수들의 총합이다. 답안 프로그램은 반드시 게임을 한 뒤 결과를 기록하고, 출력 결과가 게임의 실제 결과와 일치해야 한다.

입출력 파일의 예

다음은 어떤 게임의 처음 상태와 그에 따른 실행 결과를 나타낸 예이다.

INPUT.TXT      OUTPUT.TXT
6              15 14
4
7
9
2
2
5

2. 생산 공정의 처리

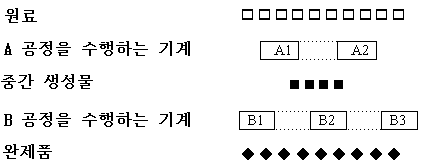
어떤 공장이 생산 라인을 운영하고 있다. 한 생산 과정에는 A와 B라는 두 가지 공정이 이루어진다. 공장에는 각각의 공정을 수행하도록 되어 있는 기계가 여러 대 있다. 위 그림은 생산라인의 구성 모습을 잘 보여주고 있다. A 공정을 하는 기계는 처음에 들어온 원료를 가공하여 이를 중간 생성물로 바꾼 뒤 이를 B 공정을 맡는 기계에 넣는다. B 공정을 하는 기계는 중간 생성물을 더 가공하여 그것으로 완제품을 만든다. 컴파일과 링크 과정을 생각하면 이해가 빠를 것이다. 단 여기서는 원료 하나가 각각 중간 생성물과 완제품의 순서로 바뀐다. 모든 기계는 서로에게 영향을 주지 않고 같은 시간에 병렬식으로 따로따로 동작한다. 각 원료의 크기는 별 제한이 없으며, 개수만이 의미가 있다. 다만 기계들은 제각기 성능이 달라, 한 개의 원료를 처리하는 시간이 기계마다 서로 다를 수 있다.

모든 기계가 작업을 동시에 시작했을 때 N개의 원료가 모두 A 과정을 마무리하는 데 필요한 가장 짧은 시간을 계산하라. 그리고 N개의 원료가 모두 완제품으로 바뀌는 데 걸리는 가장 짧은 시간도 계산하라. 이번 문제는 이를 수행하는 프로그램을 작성하는 것이다.

입력 자료

INPUT.TXT에는 다섯 줄에 걸쳐 자연수가 들어있다. 첫 줄에는 원료의 수 N(1<=N<=1000)이 들어 있다. 그리고 둘째 줄에는 A 공정을 처리하는 기계의 수 M1이 있다. (1<=M1<=30) 그리고 셋째 줄에는 M1개의 정수가 있어서, A 공정을 하는 기계 각각이 원료 하나를 중간 생성물로 바꾸는 데 걸리는 시간이 들어있다. 넷째와 다섯 째 줄도 이와 비슷한 구조로, B 공정을 처리하는 기계의 수 M2(1 M2 30)와, 이 기계들이 한 중간 생성물을 완제품으로 바꾸는 데 걸리는 시간을 나타내는 M2개의 자연수가 차례로 들어있다. 시간은 모두 단위 시간이며, 상대적인 값이다. 또한 시간 범위는 1부터 20까지이다.

출력 자료

답안 프로그램은 OUTPUT.TXT에 두 줄을 출력해야 한다. 첫 줄에는 모든 원료가 A 공정을 다 마치는 데 걸리는 최소 시간이, 둘째 줄에는 모든 원료가 완제품으로 바뀌는 데 걸리는 최소 시간이 들어간다. 답은 모두 자연수이다.

입출력 파일의 예

다음은 한 입력 파일과 그에 해당하는 출력 결과의 예이다.

INPUT.TXT       OUTPUT.TXT
5               3
2               5
1 1
3
3 1 4

3. 학교 네트워크

여러 학교들이 컴퓨터 네트워크로 연결이 되어 있다. 어떤 소프트웨어가 개발되어 한 학교로 왔을 때, 그 학교는 자기가 보내기로 되어 있는 다른 학교에게 그 소프트웨어를 네트워크로 전달하도록 학교 사이에 합의가 되어 있다. 이 과정을 되풀이하면 결국 모든 학교에 소프트웨어가 전달된다. A 학교에서 B 학교에 소프트웨어를 보내기로 되어 있는데 B 학교도 A 학교로 소프트웨어를 또 보내도록 지정되는 것과 같은 경우는 없다.

이번 문제는 두 가지다. 우선 모든 학교에 새로 개발된 소프트웨어를 보내기 위해서 처음에 그것을 보내야 하는 최소한의 학교 수를 계산하는 프로그램을 작성하는 것이다. 또한 우리는 여러 학교 중 아무 한 곳에만 소프트웨어를 보내도 결국 모든 학교가 그 소프트웨어를 공급받게 하고 싶다. 그러려면 소프트웨어 공급 네트워크 망을 최소 몇 군데 더 확장해야 하는지를 계산하는 것이 둘째 문제이다. 여기서 한 군데 확장한다는 말은 어떤 학교에서 자기가 보내기로 배당된 학교에 보낼 대상 학교를 한 곳 더 추가한다는 뜻이다.

입력 자료

INPUT.TXT의 첫 줄에는 네트워크 망에 든 학교의 개수를 나타내는 N(2<=N<=100)이 있다. 각 학교는 1부터 N까지의 수로 구분한다. 그리고 다음 N줄에는 1부터 N까지 각 학교가 소프트웨어를 보내기로 되어 있는 대상 학교의 번호가 들어있다. 각각의 목록은 0으로 끝난다. 소프트웨어를 보낼 학교가 하나도 없는 학교에 해당하는 줄에는 그냥 0만 있다.

출력 자료

OUTPUT.TXT는 두 줄이어야 한다. 첫째 줄에는 첫째 문제의 정답이 자연수로 들어간다. 둘째 줄에는 둘째 문제의 정답을 적는다.

입출력 파일의 예

다음은 한 입력 파일과 그에 해당하는 출력 결과의 예이다.

INPUT.TXT       OUTPUT.TXT
5               1
2 4 3 0         2
4 5 0
0
0
1 0

4. 특수 수열의 교환 정렬

정렬은 컴퓨터에서 매우 빈번하게 이루어지는 작업 중의 하나이다. 여기서는 크기 범위가 최대 세 단계뿐인 자료를 정렬하는 특수한 정렬 문제를 하나 생각해 보자. 이러한 경우의 예로는 올림픽 메달리스트를 메달의 순으로 정렬할 때를 들 수 있다. 금메달이 먼저 오고, 다음이 은메달, 동메달의 순이다.

이번 문제에서 사용되는 정렬 대상은 1, 2, 3만으로 되어 구성되어 있는 수열이다. 정렬 순서는 오름차순이다. 정렬 작업은 일련의 교환 작업만으로 이루어져야 한다. 교환 작업이란 수열의 번호를 나타내는 수 p, q가 있을 때 p째 원소와 q째 원소의 값을 서로 맞바꾸는 것을 말한다.

1, 2, 3으로만 이루어진 이러한 수열이 있다. 이때, 이 수열을 오름차순으로 정렬되게 하려면 최소 교환 작업을 몇 번 해야 하는지 그 횟수를 계산하는 프로그램을 작성하라. 또한 어느 위치를 교환하면 정렬되는지 교환을 하는 과정 역시 열거하도록 하여라.

입력 자료

INPUT.TXT의 첫 줄에는 수열에 든 수의 개수 N(1<=N<=1000)이 있고, 다음부터 수열의 원소(1~3)가 한 줄에 한 개씩 차례대로 들어있다.

출력 자료

OUTPUT.TXT의 첫 줄에는 이 수열을 오름차순으로 정렬하기 위해 필요한 최소 교환 횟수 L을 기록한다. 그리고 다음 L 줄에는 교환 정렬을 해 가는 과정을 순서대로 기록한다. 각 줄에는 서로 교환하는 위치를 뜻하는 두 정수가 들어있다. 위치의 범위는 1부터 N까지이다.

입출력 파일의 예

다음은 한 입력 파일과 그에 해당하는 출력 결과의 예이다.

INPUT.TXT     OUTPUT.TXT
9             4       ← 2 2 1 3 3 3 2 3 1
2             1 3     ← 1 2 2 3 3 3 2 3 1
2             4 7     ← 1 2 2 2 3 3 3 3 1
1             9 2     ← 1 1 2 2 3 3 3 3 2
3             5 9     ← 1 1 2 2 2 3 3 3 3
3
3
2
3
1

5. 가장 긴 시작 문자열 구하기

어떤 생물체의 구조는 생물체를 이루고 있는 성분을 뜻하는 대문자 알파벳 문자열로 나타낼 수 있다. 생물학자들은 이 길다란 구조 문자열을, 의미를 가진 짧은 문자열들로 분해하는 데 몰두하고 있다. '의미를 가진 짧은 문자열'을 낱말이라고 일컫겠다. 우리는 생물체의 구조를 나타내는 문자열 S는 낱말들의 집합인 P의 원소로부터 합성해 낼 수 있다고 가정한다. 무슨 말인가 하면, P의 원소로 n개의 낱말 p1, p2, ..., pn이 있다면, 이들 원소들을 임의의 순서대로 붙여 더하기만 하면 S와 같은 문자열을 만들 수 있다는 말이다. 한 낱말이 합성하는 데 두 번 이상 쓰일 수도 있으며, 집합에 있는 낱말들이 모두 다 합성하는 데 쓰일 필요도 없다. 예를 들어 ABABACABAAB라는 문자열은 다음과 같은 낱말의 집합으로 합성할 수 있는 것이다.

{A, AB, BA, CA, BBC}.

문자열 S에서 처음 K 글자를 따온 것을 '길이가 K인, S의 시작 문자열'라고 한다. 이제 낱말 집합인 P의 원소와, 생물 구조를 나타내는 문자열 T를 읽어들이는 프로그램을 작성하라. 프로그램은 T의 시작 문자열 중 P의 원소로 합성할 수 있는 가장 긴 것을 구해야 한다.

입력 자료

입력 파일은 두 개다. INPUT.TXT에는 낱말의 집합 P의 원소가 들어있다. 한편 조사 대상인 문자열 T의 내용은 DATA.TXT에 들어있다. INPUT.TXT의 첫 줄에는 P의 원소 수 N(1<=N<=100)이 있고, 각각의 원소는 두 줄에 걸쳐 들어있다. 첫 줄에는 그 낱말 원소의 길이 L(1<=L<=20)의 값이, 다음 줄에는 L글자인 실제 낱말이 들어있다. 낱말의 각 글자는 A부터 Z까지의 대문자이다. N개의 원소들은 모두 서로 다르다.

DATA.TXT의 각 줄에는 첫 칸에 성분 나열을 나타내는 알파벳 대문자가 하나씩 들어 있다. 그리고 파일 끝에 마침표가 들어가서 파일의 끝을 나타낸다. T의 길이는 최소 1부터 최대 500,000까지이다.

출력 자료

OUTPUT.TXT의 첫 줄에, T의 시작 문자열 중 P의 원소만으로 합성할 수 있는 가장 긴 것의 길이를 기록한다.

입출력 파일의 예

다음은 입력 파일 두 개와 그에 해당하는 출력 결과의 예이다. 첫 부분부터 시작하여 A/BA/BA/CA/BA/AB까지 열한 자까지를 기본 낱말만 모아서 만들 수 있다.

INPUT.TXT     DATA.TXT       OUTPUT.TXT
5             A              11
1             B
A             A
2             B
AB            A
3             C
BBC           A
2             B
CA            A
2             A
BA            B
              C
              B

6. 매직 스퀘어

루빅 씨는 루빅 큐브을 만들어 성공하고 난 뒤, 그것을 2차원 형식으로 바꾼 매직 스퀘어를 고안했다. 이것은 아래 그림과 같이 크기가 같은 여덟 개의 정사각형으로 되어 있다.

1	2	3	4
8	7	6	5

이번 문제에서 우리는 각각의 정사각형 면이 서로 다른 색으로 칠해진 매직 스퀘어를 다룬다. 각 색깔은 1부터 시작하는 8개의 자연수로 표현된다. 한편, 스퀘어의 상태를 나타내는 수열이 있는데, 이는 여덟 개의 숫자로 이루어지며 좌측 상단부터 시작해서 시계 방향으로 수열의 수를 차례대로 채워나간다. 그러므로, 매직 스퀘어의 처음 상태를 이 수열로 나타내면 (1, 2, 3, 4, 5, 6, 7, 8)이 된다. 이를 특별한 경우로, 매직 스퀘어의 처음 상태라고 규정하겠다.

매직 스퀘어에는 세 가지 변환을 가할 수 있다. 이를 차례대로 A, B, C로 구분한다. 방법은 다음과 같다.

A: 윗줄과 아랫줄에 있는 수를 바꾼다.
B: 각 줄에 있는 수를 오른쪽으로 한 칸씩 옮기고, 맨 오른쪽에 있던 수를 맨 왼쪽으로 옮긴다.
C: 가운데에 있는 네 정사각형의 수를 시계 방향으로 한 번 돌린다.

매직 스퀘어의 상태가 어떻든 다음 세 가지 변환을 시킬 수 있다.

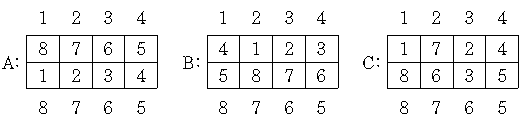
초기 상태에 있던 매직 스퀘어에 각각의 변환을 가한 결과는 위와 같다. 스퀘어 바깥에 있는 숫자는 스퀘어의 위치를 나타낸다. 만약 p 위치의 정사각형에 i라는 숫자가 있다면 이 변환을 거친 뒤 위치가 i였던 곳이 p 위치로 이동했음을 뜻한다.

이번 문제는 초기 상태에 있는 매직 스퀘어에 A, B, C 변환을 어느 횟수만큼 하여 지정한 상태인 매직 스퀘어를 만드는 동작 방법을 계산하는 프로그램을 작성하는 것이다. 또한 총 변환 횟수가 300을 넘지 않는 정답에는 특별 점수가 2점 더해진다.

입력 자료

INPUT.TXT에는 만들고자 하는 매직 스퀘어의 상태를 지정하는 8개의 자연수가 첫째 줄에 들어있다. 순서는 위에서 말한 수열의 순서이다.

출력 자료

OUTPUT.TXT의 첫 줄에는 우선 A, B, C의 총 변환 횟수 L이 들어가야 한다. 다음 L줄에는 어떤 변환부터 순서대로 시킬지를 나타내는 변환 종류가 각 줄 첫 칸에 들어간다.

유틸리티 프로그램

MTOOL.EXE는 문제 디렉토리에 마련되어 있는 프로그램으로, 응시자가 매직 스퀘어를 직접 변환시켜 보면서 퍼즐을 풀게 하는 프로그램이다. "mtool input.txt output.txt"이라고 입력하면 입력 파일의 내용과 같은 매직 스퀘어가 출력 파일의 내용대로 변환되는 단계를 보여주는 기능도 제공한다.

입출력 파일의 예

INPUT.TXT
2 6 8 4 5 7 3 1 7
 
OUTPUT.TXT
B
C
A
B
C
C
B