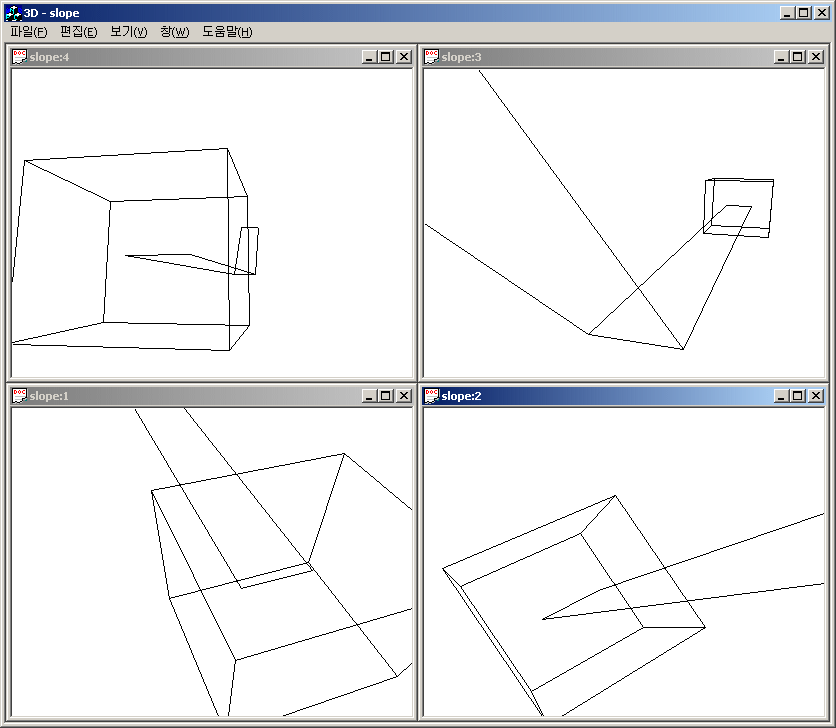
3차원 공간에서 임의의 개수의 선을 입력받아 이것을 원근법으로 평면에 표시해 주는 프로그램입니다. 화살표 키로 자유자재로 3차원 공간을 드나들며, 원하는 위치에서 원하는 각도로 물체를 볼 수 있습니다. 장면의 크기는 창 크기에 맞게 자동으로 조절됩니다. (창 크기가 정사각형이어야 화면 비율이 맞게 나옵니다)
모든 움직임은 현재 화면을 기준으로 유연하게 행해집니다. 단, Shift와 위치 이동 키를 함께 누르면 Y축 각도가 무시되어 이동합니다. (예를 들어 아래를 보면서 앞으로 가는 것이 가능해집니다.)
특히 이 프로그램은 MDI를 쓰고 있어서, 한 파일을 표시하는 창을 여러 개 만들 수 있기 때문에 아래처럼 매우 흥미로운 활용도 할 수 있습니다. 다른 어떤 라이브러리도 쓰지 않고 자체적인 수학식으로 좌표를 계산하고 기본 윈도우 API만 써서 그림을 출력하기 때문에 소스 코드는 이식성이 있습니다.
간단한 기하학 도형, 정다면체, 토러스(튜브), 구, 3차원 그래프 등 여러 재미있는 입체그림들이 예제로 같이 들어있습니다. 파일 첫 줄에 출력하고 싶은 선의 갯수를 넣고, 그 다음 선의 첫 점의 X Y Z 좌표와 끝 점의 X Y Z 좌표를 넣어 주기만 하면 입력 데이터를 얼마든지 만들 수 있습니다.
혹시 MFC71.DLL과 MSVCR71.DLL이 없어서 프로그램이 실행되지 않으면 이 압축 파일도 받아서 윈도우 시스템 폴더에 설치하시기 바랍니다.
2021년 1월, shift를 누른 상태로는 우클릭 드래그를 해서 시점 변환이 되지 않던 오랜 고질적인 문제를 해결했습니다.
2019년 9월, 예제 데이터에 3차원 그래픽 모델의 고전인 '유타 주전자'를 추가했습니다.
오랜만에 업데이트 된 2018년 11월 29일 버전은,
2005년 4월 27일 버전은,
2004년 10월 10일 버전은 (2.2),
2004년 2월 24 - 3월 1일 버전은 (2.0),
2003년 4월 26일 버전은,

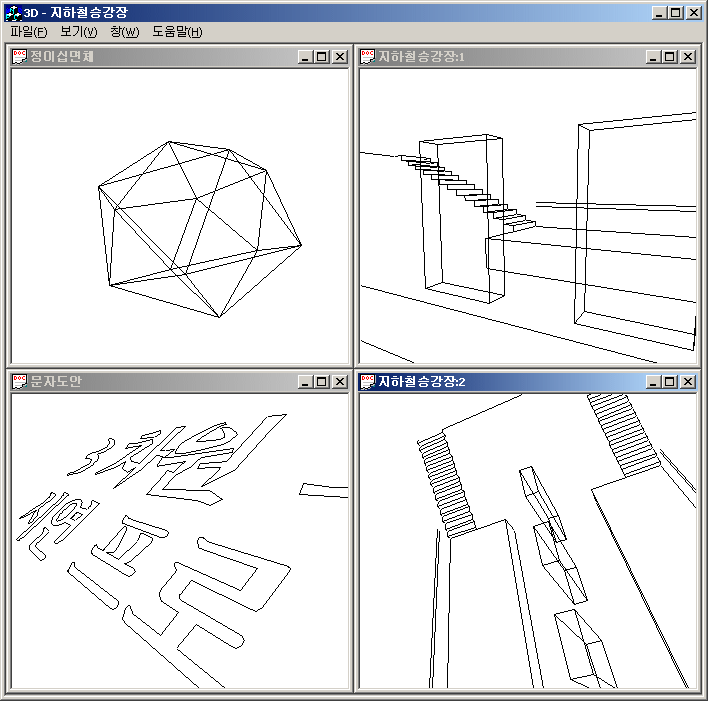
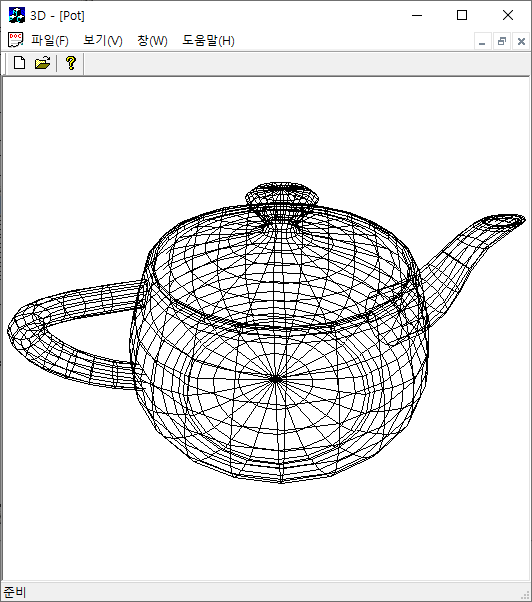
다음은 이 프로그램으로 볼 수 있는 3차원 그래픽 데이터를 생성해 주는 프로그램입니다.
원은 DELTA만한 정밀도로 표현합니다. 값이 작을수록 촘촘해집니다. M_PI/15는 15각형을 의미하지요.
int Build3dSphere()
{
#define M_PI 3.141592
#define RADIU 200
#define DX 0
#define DY 0
#define DZ 0
#define DELTA M_PI/15
FILE *fp; double a,b;
fp=fopen("d:\\구.txt", "wt");
for(b=0;b<=2*M_PI;b+=DELTA) {
for(a=0;a<2*M_PI;a+=DELTA) {
fprintf(fp, "%f %f %f ", cos(b)*cos(a)*RADIU+DX, sin(b)*cos(a)*RADIU+DY,
sin(a)*RADIU+DZ);
fprintf(fp, "%f %f %f\n", cos(b)*cos(a+DELTA)*RADIU+DX, sin(b)*cos(a+DELTA)*RADIU+DY,
sin(a+DELTA)*RADIU+DZ);
fprintf(fp, "%f %f %f ", cos(b)*cos(a)*RADIU+DX, cos(b)*sin(a)*RADIU+DY,
sin(b)*RADIU+DZ);
fprintf(fp, "%f %f %f\n", cos(b)*cos(a+DELTA)*RADIU+DX, cos(b)*sin(a+DELTA)*RADIU+DY,
sin(b)*RADIU+DZ);
}
}
fclose(fp);
return 0;
}
3차원 그래픽 시연 프로그램의 소스 코드에서 내부적으로 쓰인 C3dMatrix와 C3dPoint 클래스를 이용합니다. 새 가지의 위치는 원래의 가지의 방향을 행렬로 변환하여 얻어집니다.
void CreateBranch(const C3dMatrix& mat, const C3dPoint& pos, double lengt)
{
if(lengt<50) return;
C3dPoint newpos(0, 0, -lengt); newpos=mat*newpos+pos;
printf("%f %f %f %f %f %f\n", pos.x, pos.y, pos.z, newpos.x, newpos.y, newpos.z);
//새 정점에서 선분을 또 세 개 만들어 호출
C3dMatrix rotY(
cos(M_PI/8), 0, -sin(M_PI/8),
0, 1, 0,
sin(M_PI/8), 0, cos(M_PI/8)
);
C3dMatrix rotZ(
cos(2*M_PI/3), -sin(2*M_PI/3), 0,
sin(2*M_PI/3), cos(2*M_PI/3), 0,
0,0,1
);
C3dMatrix res=mat*rotY; CreateBranch(res, newpos, lengt*4/5);
res=mat*rotZ*rotY; CreateBranch(res, newpos, lengt*4/5);
res=mat*rotZ*rotZ*rotY; CreateBranch(res, newpos, lengt*4/5);
}
위의 경우, 한 가지에서 세 개의 가지가 원래 가지보다 22.5도 정도 굽어진 채 120도 간격으로 균일하게 뻗어 나옵니다. 길이는 원래 가지의 80%가 되지요. 초기에는
C3dMatrix mat(C3dMatrix::identity); C3dPoint pt(0, 0, 100); CreateBranch(mat, pt, 200);
이렇게 실행을 시작해 보세요.
#define fixtof(p) ( ((double)*((long *)&p))/65536.0 )
int gx, gy;
#define DELTA 0.4
void draw_qspline(POINTFLOAT a, POINTFLOAT b, POINTFLOAT c)
{
//printf("Draw spline from %g %g - (%g %g) - %g %g\n", a.x,a.y, b.x,b.y, c.x,c.y);
float p,q,r,t;
for(t=0.0;t<1.0;t+=DELTA) {
p=(a.x-2*b.x+c.x)*t*t+(2*b.x-2*a.x)*t+a.x;
q=(a.y-2*b.y+c.y)*t*t+(2*b.y-2*a.y)*t+a.y;
printf("0 %g %g ", p+gx,q+gy);
r=t+DELTA; if(r>1) r=1;
p=(a.x-2*b.x+c.x)*r*r+(2*b.x-2*a.x)*r+a.x;
q=(a.y-2*b.y+c.y)*r*r+(2*b.y-2*a.y)*r+a.y;
printf("0 %g %g\n", p+gx,q+gy);
}
}
void draw_line(float a, float b,float c,float d)
{
printf("0 %g %g 0 %g %g\n", a+gx,b+gy, c+gx,d+gy);
}
void MakeDemo(HDC hDC, UINT wr, int mx, int my)
{
MAT2 mat2={{0,5},{0,0},{0,0},{0,-5}}; GLYPHMETRICS gm; PSTR buf; DWORD dwSize;
dwSize=::GetGlyphOutline(hDC, wr, GGO_NATIVE, &gm, 0, 0, &mat2);
buf=new char[dwSize]; gx=mx, gy=my;
::GetGlyphOutline(hDC, wr, GGO_NATIVE, &gm, dwSize, buf, &mat2);
//now, render the glyph data
TTPOLYGONHEADER *ptth; TTPOLYCURVE *ppc; int i,pos=0;
POINTFLOAT pa={-999,-999},pb,pc, totalbegin, totalend;
do {
ppc=(TTPOLYCURVE *)(buf+pos);
if(ppc->wType!=TT_PRIM_LINE && ppc->wType!=TT_PRIM_QSPLINE) {
ptth=(TTPOLYGONHEADER *)(buf+pos);
if(pa.x!=-999)
draw_line(totalbegin.x, totalbegin.y, totalend.x, totalend.y);
pa.x=fixtof(ptth->pfxStart.x); pa.y=fixtof(ptth->pfxStart.y);
totalbegin=pa;
pos+=sizeof(*ptth); ppc=(TTPOLYCURVE *)(buf+pos);
}
switch(ppc->wType) {
case TT_PRIM_QSPLINE:
for(i=0;i<ppc->cpfx-1;i++) {
pb.x=fixtof(ppc->apfx[i].x); pb.y=fixtof(ppc->apfx[i].y);
if(i<ppc->cpfx-2) {
pc.x=(pb.x+fixtof(ppc->apfx[i+1].x))/2;
pc.y=(pb.y+fixtof(ppc->apfx[i+1].y))/2;
} else {
pc.x=fixtof(ppc->apfx[i+1].x);
pc.y=fixtof(ppc->apfx[i+1].y);
}
draw_qspline(pa,pb,pc);
pa=pc; totalend=pa;
}
break;
case TT_PRIM_LINE:
for(i=0;i<ppc->cpfx;i++) {
pb.x=fixtof(ppc->apfx[i].x);; pb.y=fixtof(ppc->apfx[i].y);
draw_line(pa.x,pa.y, pb.x,pb.y);
pa=pb;
}
totalend=pa;
}
pos+=sizeof(*ppc)+sizeof(POINTFX)*(ppc->cpfx-1);
}
while(pos<dwSize);
if(pa.x!=-999) draw_line(totalbegin.x,totalbegin.y, totalend.x,totalend.y);
delete []buf;
}
원하는 글꼴 오브젝트가 설정되어 있는 HDC 핸들과, 만들고 싶은 글자의 유니코드 번호를 wr에 지정하여 MakeDemo 함수를 호출하면 됩니다.
void CCubicBezierCurveOn3D(double t, const C3dPoint *ctrlpt, C3dPoint& o)
{
double _t = 1 - t;
double coef[4] = {
_t * _t * _t,
3 * t * _t * _t,
3 * t * t * _t,
t * t * t
};
for (int q = 0; q < 3; q++) {
double C3dPoint::* mptr = (q == 0 ? &C3dPoint::x : q == 1 ? &C3dPoint::y : &C3dPoint::z);
o.*mptr = ctrlpt[0].*mptr * coef[0] + ctrlpt[1].*mptr * coef[1] + ctrlpt[2].*mptr * coef[2] + ctrlpt[3].*mptr * coef[3];
}
}
void CCubicBezierPlaneOn3D(double ty, double tx, const C3dPoint (*ctrlpt)[4], C3dPoint& o)
{
double _ty = 1 - ty, _tx = 1 - tx;
double C_y[4] = {
_ty * _ty * _ty,
3 * ty * _ty * _ty,
3 * ty * ty * _ty,
ty * ty * ty
};
double C_x[4] = {
_tx * _tx * _tx,
3 * tx * _tx * _tx,
3 * tx * tx * _tx,
tx * tx * tx
};
for (int q = 0; q < 3; q++) {
double C3dPoint::* mptr = (q == 0 ? &C3dPoint::x : q == 1 ? &C3dPoint::y : &C3dPoint::z);
o.*mptr = 0;
for (int y = 0; y < 4; y++)
o.*mptr += ctrlpt[y][0].*mptr * C_y[y] * C_x[0] + ctrlpt[y][1].*mptr * C_y[y] * C_x[1] +
ctrlpt[y][2].*mptr * C_y[y] * C_x[2] + ctrlpt[y][3].*mptr * C_y[y] * C_x[3];
}
}
곡선 버전은 제어점 4개의 배열을 ctrlpt에 넣고 0 이상 1 이하의 매개변수 t를 주면 그 지점에 해당하는 궤적 o를 얻을 수 있습니다.
곡면 버전은 제어점 4개로 이뤄진 베지어 곡선 자체를 4개 받습니다. 이를 주고 매개변수도 y축과 x축 2개를 주면 그 지점에 해당하는 궤적 o를 얻을 수 있습니다.