한자어로 '원'이라고 부르는 동그라미라는 도형은 시각적으로나 수학적으로나 아주 신기한 도형이다.
둥글다는 게 무슨 의미인지 기계가 계산으로 표현할 수 있을 정도로 엄밀하게 정의하자면 결국 '어떤 점에서 거리가 같은 점들의 집합'이라는 정의가 등장하게 되고, n차원 직교 좌표에서 거리라는 건 결국 차원을 구성하는 각 축의 거리들의 제곱의 합의 제곱근이라고 정의된다.
원의 지름과 원의 둘레의 비율은 그 이름도 유명한 '파이'이며, 3.141592... 로 시작하는 이 값은 무리수인 동시에 초월수라는 것도 상식이다.
그런데 이 원을 정사각형 격자 모양의 래스터 그래픽 장치에서 어떻게 하면 효율적으로 그릴 수 있을까? 그런 물건의 내부엔 컴퍼스 같은 직관적인 도구가 없는데 말이다.
중심이 x, y이고 반지름이 r인 원을 구성하는 좌표들을 어떤 계산을 통해 얻어 올 수 있을까?
원점이 중심인 원의 방정식은 x^2+y^2=r^2. 따라서 y=sqrt(r^2-x^2) 방정식을 이용하면 사분원 내지 반원을 구성하는 점을 구할 수 있다. 그리고 이 값을 바탕으로 나머지 방향의 점을 그리면 될 것이다.
#include <math.h>
template<typename T>
void Draw_Circle(int x, int y, int r, T f)
{
double R_2 = r*r;
for(int i=0;i<r;i++) {
int v = (int)(sqrt( R_2 - i*i )+0.5);
f(x-i, y-v); f(x-i, y+v);
f(x+i, y-v); f(x+i, y+v);
}
}
for문 자체는 0부터 r까지 사분원의 x좌표만 돌고, 이를 바탕으로 점을 찍는 함수 f를 4개 방향으로 모두 호출한다.
r의 제곱 값은 한 번만 계산하면 되므로 for문 밖에서 별도로 선언해 주는 센스도.
소숫점은 버림이 아니라 반올림이 되도록 0.5를 더한 뒤에 int로 캐스팅하는 게 좋다. 그래야 당장 그려지는 원도 90*n도 부근이 더 탱탱하고 보기 좋아진다.
함수의 사용은 MFC 기준으로 이런 식으로 하면 된다. 함수 안에서 또 다른 함수를 내부적으로 호출할 때 함수 포인터보다 람다가 참 깔끔하긴 하다. (너무 남발한 게 꼬이면 code bloat은 피할 수 없겠지만)
CPaintDC dc(this);
auto x = [&](int x,int y) { dc.SetPixel(x,y,0); };
Draw_Circle(220,220, 200, x);
Draw_Circle(420,330, 160, x);
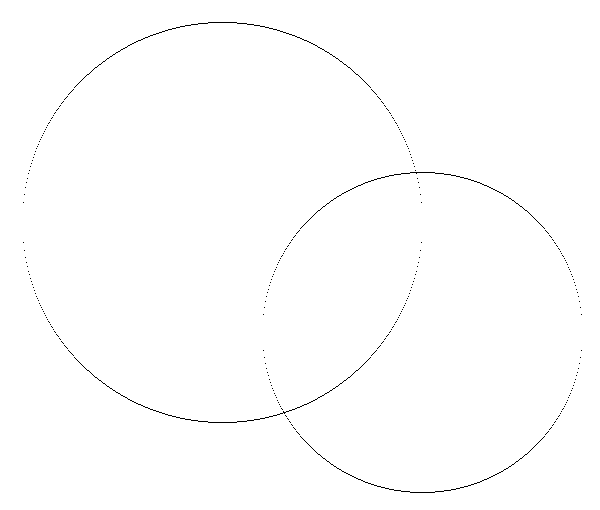
그런데 아뿔싸, 역시 기울기가 1보다 더 커지는 곳에는 점이 듬성듬성 떨어져 있게 된다.
이 틈을 점 찍기가 아니라 선 그리기 같은 다른 함수로 메운다는 건 있을 수 없는 일이고..
결국, 우리의 원 그리기 알고리즘은 언제나 기울기가 1보다 작은 구간에서만 동작하게 loop 구조를 바꿀 필요가 있다.
우리는 원을 4등분했는데, 그렇게 4등분된 조각도 한쪽 끝과 맞은편 끝이 완벽하게 대칭으로 이들을 동시에 그려 보자.
가령, 1사분면에서는 x좌표를 1씩 증가시키면서 r로 근접하고(위의 코드에서 i) y좌표는 r이다가 점점 0으로 작아지는데(위의 코드에서 v),
이와 동시에 반대편에서는 y좌표를 1씩 증가시키면서 r로 근접하고, x좌표는 r에서 0으로 근접시키도록 점을 같이 그리는 것이다.
이제 loop는 변수 i의 값이 r에 도달한 지점에서 끝나는 게 아니라 v와 값이 같아지는 지점에서 끝나면 된다. (정확히는 sqrt(2)*r/2 지점이 됨)
{
double R_2 = r*r;
for(int i=0; ;i++) {
int v = (int)(sqrt( R_2 - i*i )+0.5);
f(x-i, y-v); f(x-v, y-i);
f(x-i, y+v); f(x-v, y+i);
f(x+i, y-v); f(x+v, y-i);
f(x+i, y+v); f(x+v, y+i);
if(i>v) break;
}
}
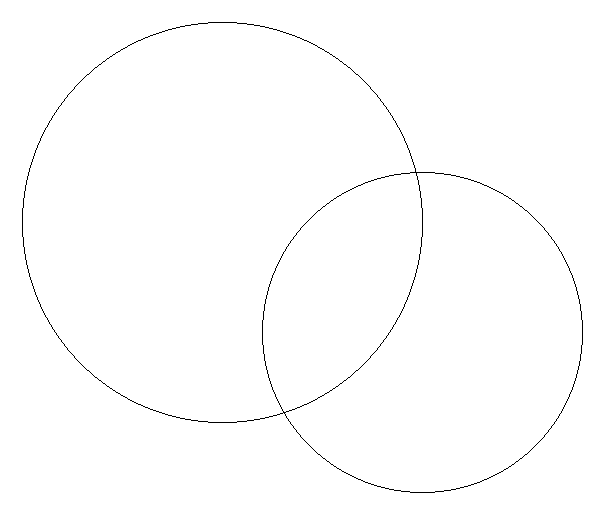
그러나 이런 원 하나 그리는데 부동소숫점에, 곱셈에, 심지어 제곱근까지 꽤 부담스러운 연산이 많이 들어갔다.
이걸 좀 줄일 수는 없을까?
...
int R_2 = r*r;
int v = r;
for(int i=0; ;i++) {
if(i*i + v*v > R_2) --v;
...
loop의 앞부분을 이렇게 고쳐 보자.
x축에 속하는 i의 값이 1증가할 때마다 y축에 속하는 v의 값은 그대로 유지되거나 1 감소하거나 둘 중 한 변화만을 겪을 것이다.
i가 증가함에 따라 원점에서 i, v까지의 거리가 R보다 확 커지게 됐다면, 이 궤적은 원의 범위를 벗어나는 것이므로 y축에 속하는 v를 1 줄여 준다.
실질적으로 행해지는 연산을 이렇게 최적화해 주면 최소한 부동소숫점과 제곱근 연산은 없어진다.
그러나 최적화의 여지는 그래도 여전히 남아 있다. 저 꼴도 보기 싫은 곱셈을 없애려면 어떡하면 좋을까?
방법이 있다.
결국, i*i는 0, 1, 4, 9, 16 ...의 순열을 생성해 낼 텐데, 얘는 덧셈을 두 번 하는 걸로 대체할 수 있다. 한 번 덧셈을 한 뒤엔 증가치가 2씩 늘어나니까 말이다(1과 4의 차는 3, 4와 9의 차는 5, 9와 16의 차는 7). x^2의 도함수가 괜히 2*x가 아니다.
그리고 v는 초기값이 아예 R_2와 같으니 약분이 가능하다. 그 뒤에 v의 값이 줄어들면서 차이만이 발생할 뿐이다. 그런데 얼마를 빼 줘야 할까?
x^2가 (x-1)^2로 바뀌었을 때 감소하는 값은 잘 알다시피 2*x-1이다. 따라서 이 값만 초기에 계산해 놓은 뒤, v가 1 감소하게 됐을 때 가상의 v_square은 그만치 빼 주고, 그 델타값 자체도 2 감소시키면 된다.
...
int v = r, i_square = 0, i_delta = 1;
int v_delta=2*r-1, v_square_delta = 0;
for(int i=0; ;i++) {
if(i_square + v_square_delta > 0) {
--v; v_square_delta-=v_delta, v_delta-=2;
}
... //점 여덟 군데를 찍어 준 뒤
if(i>v) break;
else i_square+=i_delta, i_delta+=2;
}
이로써 그 부드러운 원을 오로지 정수의 덧셈만으로, 그리고 곱셈이라고는 loop 돌기 전에 *2 단 한 번밖에 안 하는 깔끔한 원 그리기 알고리즘이 완성되었다. 놀랍지 않은가? 게다가 고정적인 두 배 연산은 잘 알다시피 bit shift로도 수행 가능한 아주 가벼운 연산이기도 하고 말이다.
GWBASIC, Windows GDI API, 옛날 볼랜드 BGI 등 모든 그래픽 라이브러리에 들어있는 원 그리기 함수는 기본적으로 이 알고리즘을 이용하여 원을 그린다. 각종 알고리즘 서적에 예제로 실려 있는 소스들도 세부적인 변수 활용이나 계수 계산에 차이가 있을지언정 기본적인 아이디어는 동일하다.
사실, 이건 거의 대학교 학부 수준이고 정보 올림피아드 공부라도 했다면 중· 고등학교 시절에라도 접했을 기초적인 내용이다. 진짜 어려운 건 이걸 응용하여 안티앨리어싱을 적용한다거나 타원을 그리거나, 아예 부채꼴 내지 회전된 원을 그리는 알고리즘이다.
단, Windows GDI가 그리는 원은 왠지 좀 엉성하고 덜 예쁜 것 같다. 비교를 할 때 반올림 보정을 안 하는지 경계가 아주 약간 덜 통통하며, 특히 기울기가 1(45도)에 가까워지는 지점에 점의 배치가 지저분하다.
차이를 보이기 위해 움짤을 만들어 보았다. 파란색 원은 GDI 함수로 그린 것이고, 빨간색 원은 우리가 작성한 함수로 그린 것이다.
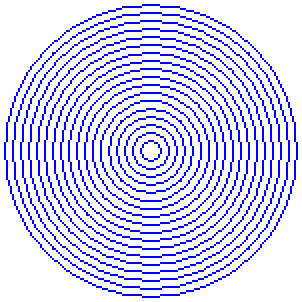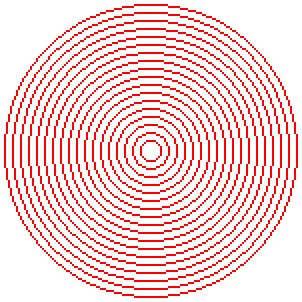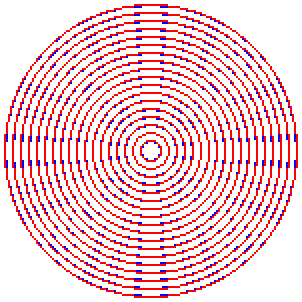
Posted by 사무엘


