김 용묵의 절대공간 - 블로그

컴퓨터 업계에서 인텔의 경쟁사라고 하면 가장 먼저 (1) 동급의 x64 CPU를 만들어서 경쟁하는 AMD,
(2) 아키텍처 차원에서 x64에 도전하는 ARM 내지 애플, 혹은 심지어 (3) 울나라 삼성 전자까지 떠올릴 수 있다. 인텔이 메모리 반도체에도 손을 뻗치고 있기 때문이다.
그런데 인텔은 저것들보다는 대외 인지도가 낮은 분야에서 AT&T와도 경합한 게 좀 있었다.

1. 바이너리: 오브젝트 파일 포맷

C/C++ 언어로 코딩을 한 뒤에 컴파일을 돌리면 생기는 자잘한 obj 파일들 말이다. 기계어 코드를 담는 이 컨테이너 껍데기의 포맷은 누가 언제 제정했을까?
x86 진영에서는 CPU 본가인 인텔에서 제정한 OMF 방식이 16비트 시절부터 널리 쓰였다. 볼랜드니 마소니 컴파일러가 다르더라도 obj 파일은 호환됐기 때문에 툴을 달리하여 링크가 가능했다.

그러나 마소에서는 32비트 Windows NT를 개발하면서 실행 파일 포맷을 바꾸고(NE에서 PE), 빌드 툴체인도 싹 갈아치웠다. 단순히 OMF의 32비트 확장을 쓰는 게 아니라 obj/lib의 포맷도 AT&T에서 제정한 COFF 방식으로 바꿨다. 그 반면, 볼랜드 컴파일러들은 32비트에서도 여전히 OMF 방식을 쓰면서 서로 파편화가 발생하게 됐다.

그 시절에 마소에서는 빌드를 더 편하게 하기 위해서, 로딩을 더 빠르게 하기 위해서(메모리 매핑), 거기에다 이식성까지 고려해서 같은 여러 명분으로 COFF를 도입했었다. 다만, 지금은 그런 명분이 기술적으로 많이 옅어지고 사라지기도 했다.

그러고 보니 GNU 툴킷의 도스용 버전에 속하는 djgpp 컴파일러도 라이브러리· 오브젝트 파일 포맷은 COFF 방식이었던 걸로 기억한다. 바이너리 에디터로 들여다보면 arch! 앞에 이런 문자열이 있고.. "이건 마소 진영과 오픈소스 진영이 공통이네?" 이런 생각을 예전에 했었다.

2. 텍스트: 어셈블리어 문법

자기네 x86 기계어를 간단한 숫자와 영단어 나열만으로 풀어서 표기하는 어셈블리어 말이다. 이것도 인텔 식 문법과 AT&T 식 문법이 공존한다. 이건 단순히 '어셈블러' 제조사 간의 문법 차이가 아니라 '어셈블리어' 차원에서의 더 저수준 차이점이다.

간단하게는 숫자 앞에 $, 레지스터 이름 앞에 %가 막 붙어 있는 게 AT&T 문법인데, 본인 역시 Visual C++이 표시해 주는 인텔 문법에만 익숙하다. 하지만 역시 리눅스 진영 gdb 같은 데에서는 AT&T 문법이 주류이다.
현업에서 어셈블리어를 직접 짤 일은 없지만, 그래도 프로그램을 디버깅 하다 보면 디버거가 디스어셈블리해 준 어셈블리어 코드를 보게는 된다.

마소는 이거 문법은 딱히 AT&T 식으로 갈아타지 않았고 인텔 문법을 고수하는 듯하다. Macro Assembler 같은 기존 제품과의 호환 문제가 있기 때문인 듯하다.
뭐, 어차피 같은 CPU 아키텍처이고, 짜는 게 아니라 읽기만 한다면야 자잘한 표기 차이는 그렇게 심각한 차이점은 아닐 것이다.

프로그래밍 언어라는 건 적당히 고급 언어를 표방하면서 실용성을 갖춘 게 인기를 얻고 대중화되는 편이다.
그럼 실용성 대신에 한쪽으로 특화된 언어는 (1) 함수형처럼 수학 내지 순수주의 쪽으로 특화되거나, 아니면 (2) 어셈블리어처럼 기계 지향적인 쪽으로 특화되는 것 같다.

한 소프트웨어의 모든 코드를 저런 특화 언어만으로 작성하는 건 아무래도 무리이다.
그래서 기존의 실용적인(?) 다중 패러다임 언어들은 저 (1), (2)의 특성을 제한적으로 부분적으로 제공하곤 한다. 그게 (1) 람다 아니면 (2) 인라인 어셈블리인 셈이다.;;

요즘 세상에 대학교 컴공과에서 어셈블리어 코딩 실습을 하는 건 군대에서 총검술, 사관학교에서 승마 실습을 잠깐 하는 것과 아주 비슷한 모양새인 것 같다.
비록 현대의 전장이나 현대의 소프트웨어 개발 방법론과는 완전히 동떨어져 버렸지만, 코딩이라는 전투에서 백병전이 어셈블리어 실습이 아니겠나..;; =_=;; 실무에서는 쓸 일이 없지만 컴공 엔지니어를 양성한다는 학교에서는 컴퓨터의 밑바닥 모습을 이런 식으로라도 경험시켜 줄 필요가 있을 것이다.

Posted by 사무엘

1990년대 초에 바다 건너 미국에서는 바둑, 오목, 체스, 스크래블 같은 보드 게임의 AI 위주로 ‘컴퓨터 올림피아드’라는 대회가 잠깐 개최된 적이 있었다. 기억을 정말 오랜만에 다시 떠올린다. ㅠㅠㅠㅠ
IOI라고 불리는 '국제 정보 올림피아드'와 헷갈리지 마시길. 요즘은 저걸 검색하면 구글도 자꾸 IOI 쪽으로 안내하는 것 같은데 그거랑은 다르다. 컴올은 공식 명칭에 '국제 I'라는 말이 없다. ㄲㄲㄲㄲ

IOI는 대학에 진학하지 않은 중등 수준의 10대 청소년들이 문제 푸는 프로그램을 '즉석에서 작성'해서 그 코드의 성능과 정확도를 평가 받는 대회이다. 그 반면, 저건 현업에 종사하는 소프트웨어 개발자/개발사들이 오랫동안 미리 연구 개발해 놓은 자기 자기 제품의 AI 성능을 현장에서 겨루는 대회이다. 즉, 로봇 쥐 미로 찾기와 비슷하며, 저런 보드 게임을 사람이 아니라 컴퓨터끼리 대국한다는 차이가 있다.

근데 컴터 올림피아드도 첫 대회가 1989년부터 시작됐다니.. 그건 IOI와 동일하다. 그리고 가끔은 IOI에서도 간단한 게임을 진행하는 프로그램을 작성해서 주최측 AI와 대국하고 채점되는 형태의 문제가 나오기는 한다. 그러니 둘이 완전히 다른 별개 분야의 대회까지는 아니긴 하다.

본인이 저 대회에 대해 들어 본 건.. 한때 왕년에 영단어 보드 게임인 스크래블의 AI를 연구하느라 관련 자료를 많이 찾아봤었기 때문이다.
무려 1988년에는 World's fastest Scrabble program (by 앤드루 아펠, 가이 제이콥슨)이라는 논문이 CACM에 게재돼서 후대의 스크래블 AI 개발자에게 아주 큰 영향을 줬다. 모든 가능한 수를 찾는 기본 작업은 이 논문에서 소개된 알고리즘으로 해치우고, 그 뒤에 단순히 당장 점수가 가장 높은 수를 넘어 장기적인 이익을 따지는 건 전략과 휴리스틱의 영역으로..

오래된 생각이긴 하다만, 스크래블 게임의 컴퓨터 구현은 대학교 수준의 자료구조와 알고리즘 코딩 주제로 아주 적합하다. 만약 내가 학원이나 학교에서 저런 전공 과목을 가르칠 기회가 있다면 실습이나 과제로 저걸 꼭 넣었지 싶다. =_=;;
하긴, 석사 논문으로 두벌식 한글 연속입력 오토마타를 연구했던 모 교수님은 자기가 강의하는 형식언어와 오토마타 수업 시간에 한글 입력 오토마타를 구현하는 과제를 고정 편성으로 넣었더구만.. 그런 것처럼 말이다.

아무튼 그건 그렇고..
저 논문을 투고했던 연구진은 딱 이듬해인 1989년, 제1회 컴퓨터 올림피아드의 스크래블 부문에 참가해서 우승했다고 한다. 타이밍 절묘하군..

그 뒤 2회와 3회에서는 Jim Homan이라고 MIT 출신의 다른 엄친아 공돌이가 개발한 스크래블 AI가 2년 연속 우승을 차지했다. 정황상, 아마 저 논문 내용을 바탕으로 AI를 더 발전시킨 것 같다.
그리고 그 사람은 저 AI 엔진을 토대로 CrossWise라는 굉장히 깔끔한 크로스워드 게임(설정을 맞춰서 스크래블 게임도 가능한!!) 프로그램을 개발해서 판매했다.

그것 말고 브라이언 셰퍼드라는 사람이 개발한 Maven이라는 스크래블 AI도 유명했다. 얘도 개발 역사가 1980년대로 거슬러 올라갈 정도로 오래됐고, 스크래블 보드 게임의 총판사에서는 Maven을 공식적으로 밀었다고 하는데.. 얘에 대해서는 나도 더 아는 바가 없다. 이쪽은 딱히 컴올에 참가한 이력도 없는 것 같다.

뭐, 이것도 다 지난 얘기이다. 지금은 스크래블 게임쯤이야 폰이나 웹에서도 돌릴 수 있을 텐데.. 유행이 지난 것 같다.
하다못해 바둑조차도 세계를 석권해 버린 알파고 개발진이 "이젠 바둑은 더 연구할 게 없다~~" 명목으로 발을 뺐을 정도이니 말이다. -_-;;

저 컴퓨터 올림피아드는 스폰서 내지 운영진을 섭외할 수 없어서 1991년 이후부터 1990년대 내내 맥이 끊겼다. 그러다가 2000년대 이후부터 다시 개최는 되고 있지만.. 다들 아시다시피 인지도가 별로 없고 마이너하다는 냄새가 풍긴다. 고전적인 최적화나 휴리스틱 위주의 AI는 유행이 끝나고 닥치고 인공신경망이 대세가 돼서 그런지..??

우리나라에서 보드 게임 AI 외길을 가고 있는 제품은 '장기도사'가 유일하지 싶다. 의미 있는 연구이긴 하다만, 보드 게임이라는 장르 자체도 마이너해지고, AI 패러다임도 마이너해져서 수요가 무척 적을 것 같다. 뭐, 그런 식으로 염세적으로만 따지자면 본인의 주특기인 세벌식 자판도 마이너 중의 초 마이너이긴 하다만 말이다. -_-;;

고전적인 AI 대신 2010년대를 풍미했던 건 인공신경망들이었다. 2012년, 사물 인식을 기가 막히게 잘한다는 AlexNet부터 시작해서 VGG, ResNet, YOLO가 뒤를 잇고 chatGPT, transformer 등등이 쏟아져 나왔으니까.
컴퓨팅 패러다임이 싹 달라졌다. 이 과정에서 파이썬은 머신러닝 학계와 업계의 공용 언어가 되었고, 교육과 실무를 다 장악해 버렸다. ㄷㄷㄷㄷ 파이썬과 루아(Lua)가 처지가 극과 극으로 달라지게 될 줄은 20년 전엔 정말 예상할 수 없었다. 이것도 생각할 점이라 하겠다.

글을 맺기 전에 잠깐.. 그러고 보니 World Cyber games도 생각난다. 얘는 컴퓨터 AI가 아니라 사람이 겨루는 대회이지만, 그래도 E-스포츠 전문이니 뭔가 컴퓨터스럽고 사이버틱한 느낌이 나기 때문이다.
얘도 2001년에 처음으로 시작됐다가 2010년대엔 스폰서를 못 구해서 한동안 중단됐던 적이 있다. 그 뒤 지금은 재개되기는 했지만 권위나 인지도가 예전만 하지는 않다는 게 컴퓨터 올림피아드와 비슷해 보인다.

Posted by 사무엘

디지털 컴퓨터가 취급하는 데이터라는 건 (1) machine word 하나에 다 들어가고 함수 인자에 값이 그대로 전해지는 primitive type이 아니면.. (2) 별도의 메모리를 할당해서 저장하고, 평소엔 그 메모리 주소를 가리키는 포인터만 대신 취급하는 complex type 이렇게 둘로 나뉜다.
그럼 primitive type은? (1) 정수, (2) 포인터, (3) 아니면 부동소수점으로 종류가 크게 나뉘는 것 같다.

문자열은 complex type이고, 문자 하나는 정수라는 primitive type에 속한다.
포인터는 물리적인 형태는 정수와 다를 바 없지만 그 숫자값의 성격, 의미와 용도가 여느 정수와는 전혀 다르다. 그리고 특정 프로그래밍 언어 이념이나 프로그래머의 편의를 구현하기 위해, 무슨 오프셋이나 카운터 같은 부가 정보를 곁들인 약간 뚱뚱한 포인터도 있다. (스마트 포인터, 자기 함수나 클래스의 바깥 문맥도 지원하는 포인터, 다중 상속을 지원하는 멤버 함수 포인터 등등~)

다음으로 부동소수점이 있다. 얘 역시 완전 별개의 영역이다. 얘는 잘 알다시피 과학 시간에 배우는 x.xxxx * 10^yy 이러는 숫자 표기법을 2진법 기반으로 컴퓨터에다 구현한 것이다. x를 mantissa, y를 exponent라고 한다.
얘는 딱딱 떨어지는 이산적인 정보를 좋아하는 컴퓨터에다가 현실의 연속적인(실무 또는 수학 계산) 계산값을 표현하려 애쓴 근성의 산물이다.

부동소수점은 자리수와 관계 없이 유효숫자가 일정하게 보장된다. 그렇기 때문에 -1 ~ 1 사이의 0.xxx 구간이 압도적으로 제일 정밀하다. 32비트건 64비트건, 부동소수점으로 표현 가능한 수의 무려 절반이 -1과 1 사이에 치우쳐 있다. 절대값 1 이상인 양수 지수부와, 그렇지 않은 음수 지수부가 반반씩이니까 말이다~!!

그리고 그 안에서도 0과 0.5 사이에 표현 가능한 수와 0.5와 1 사이에 표현 가능한 수는..?? 지수부의 크기에 비례해서 수백 배 이상 폭발적으로 차이가 난다. 이게 부동소수점의 심오한 세계이다. =_=;;
숫자가 커질수록 표현 가능 구간이 급격히 듬성듬성해지니.. 가장 흔히 쓰이는 축에 드는 32비트 single 부동소수점 기준으로 숫자가 1700만 정도로 커지고 나면 정밀도가 1이 되어 정수와 다를 바 없어진다.

또한, 1/2^n 형태가 아닌 모든 소수점은 원래 형태 그대로 정확하게 표현되지 못하고 유효숫자 이후의 뒷부분이 버려진다. 이 점 역시 감안해야 한다.
부동소수점 숫자를 하나 받아서 이 수의 바로 다음 크기인 수를 구하는 알고리즘을 구현해 보면 어떨까 싶다..;;

이 외에도.. x86에서는 정수끼리 나눗셈을 시키면 몫과 나머지가 같이 구해져서 레지스터에 저장된다. 그리고 0으로 나누는 건 CPU 차원에서의 오류/예외로 처리된다.
그러나 부동소수점에서의 나눗셈은 나머지라는 개념이 없다. 그리고 0으로 나눈 결과는 그냥 NaN이라는 값으로 처리된다. 이런 식으로 서로 관점과 동작이 차이가 있다.

초기화되지 않은 부동소수점 변수는 프로그래밍 언어 차원에서 NaN으로 초기화하는 게 한 가지 방법일 것 같다. NaN이 '쓰레기값' 역할을 수행하는 셈인데.. 내 기억으로 D 언어가 이걸 실제로 수행한다고 한다.
그리고 IEEE754 부동소수점 규격을 보면 NaN도 아직 에러까지는 아닌 quiet NaN, 그리고 에러인 signalling NaN으로 나뉘어 있다.

현실의 프로그래밍 언어에서는 IEEE32 (single, float) 내지 64 (double) 이 둘만을 제일 많이 볼 것이다. 당장 마소 Excel이 취급하는 숫자의 자료형만 해도 64비트 double이다.
그러나 사실은 표준 규격으로나 역사적으로는 이보다 더 다양한 부동소수점 규격이 존재한다.

같은 공간 안에서 유효숫자 개수와 표현 가능한 자리수 구획을 정하는 건 꽤 미묘한 고민거리인 것 같다. 한 가지 확실한 건 전체 공간이 커지더라도 exponent는 그에 비례해서 쭉쭉 커질 필요가 없으며, 로그함수 급으로 아주 느리게 증가해도 된다는 것이다. (비율이 갈수록 작아짐) 말 그대로 2의 exponent 승만큼의 자리수를 표현할 수 있기 때문이다.
exponent가 8만 돼도 0이 38개나 붙은 자리수를 표현할 수 있고, 바이트 경계가 딱 나뉘어서 처리하기 편하다. 그렇기 때문에 어지간한 부동소수점 규격들이 얘를 8비트로 잡은 걸 볼 수 있다.

MBF는 오늘날 같은 IEEE754 표준 규격이란 게 등장하기 전, 1980년대 마소의 BASIC 언어에서만 독자적으로 쓰였던 규격이다. 빌 게이츠와 폴 앨런이 젊은 시절에 나름 이런 것까지 독자적으로 만들어서 구현했다니..
MBF32는 IEEE32와 공간 크기와 분배 배율이 동일하지만, 비트 배치 순서가 다르다. 그렇기 때문에 서로 바이너리 차원에서 곧바로 호환되지는 않는다.

mantissa와 exponent 모두 내부적으로 부호 비트가 존재한다. 전자의 부호는 표현하는 숫자 자체의 양-음 여부를 결정하며, 후자의 부호는 숫자가 1보다 큰지 여부를 결정하게 된다.
저 표에서 mantissa-1을 3.3으로 나누면 (3.3의 의미는 ln(10)/ln(2)의 근사값) 10진법 기준의 유효숫자 개수가 나온다.
그리고 표현 가능한 범위도 exponent-1을 3.3으로 나누면 10진법 기준의 표현 가능 최대 자리수가 나온다.

맨 위의 16비트 부동소수점은 half-precison floating point라고 불리는데, 유효숫자가 3개밖에 안 되고 5비트짜리 exponent로는 최대 자리수도 겨우 10000대밖에 안 된다. 그러니 실용적인 가치는 매우 낮지만 이런 숫자도 머신러닝 계산용으로는 쓰이는가 보다. 그렇기 때문에 FP16이라는 옵션도 있는 거겠지?
그리고 볼랜드의 16비트 파스칼 컴파일러에만 전무후무 존재했던 6바이트 Real은 존재가 참 독보적이다. 4도 8도 아닌 그 중간.;;

부동소수점은 그 구조상 숫자 2개를 조합해서 한 숫자를 표현하니, 각종 산술 연산이나 비교 따위가 정수를 취급하는 것보다 무겁고 부담스럽다. 특히 자칫 잘못하면 동일한 숫자를 표현하는 방식이 여러 개 존재할 수 있게 되니, 이를 방지하기 위해서 자리수를 일정하게 맞추는 '정규화'라는 규칙이 필요하다.
그리고 부동소수점 연산은 초딩 시절에 배웠던 어림셈과 비슷한 면모가 있다. 아주 큰 수에다가 아주 작은 수를 많이 더하면 오차가 쌓이고 결과가 안 좋아진다.

쌍팔년도 시절엔 부동소수점 연산을 하드웨어 가속으로 보조해 주는 CPU 애드온이 별도로 존재했다. 일명 FPU, 코프로세서.. 그 시절엔 이거 하나만으로도 존재감과 가격이 지금으로 치면 고급 게임용 GPU나 마찬가지였다.

286~486 시절엔 모든 컴퓨터에 코프로세서가 있는 게 아니었다(486은 제일 저가 깡통 모델인 SX만). 그렇기 때문에 그 시절의 컴파일러들은 부동소수점의 처리 방식을 지정하는 옵션이 있었다. 무슨 x87을 지원할지, 그런 FPU 코프로세서가 없는 경우를 대비한 소프트웨어 연산 처리 코드를 넣을지를 말이다. =_=;;

자고로 컴퓨터 프로그램이라면 정수나 포인터를 어떤 형태로든 취급하지 않고 동작한다는 건 거의 불가능하다.
그러나 부동소수점을 전혀 취급하지 않는 프로그램은 분야에 따라서는 얼마든지 있을 수 있다. 그러니 부동소수점을 더 빠르게 다루는 건 소프트웨어로나 하드웨어로나 오랫동안 추가 옵션으로 간주되었던 것이다.

하드웨어 현질 없이 소수점 연산을 빠르게 하기 위해서 고정소수점이라는 편법도 쓰였다. 기존 정수에다가 자리수만 기계적으로 옮기고 곱셈과 나눗셈 결과를 보정하는 것 말이다. 32비트 정수를 16:16 내지 26:6 이런 식으로 분할했다. 단점과 한계가 명백하지만 이게 성능 하나는 워낙 탁월하니.. 옛날 게임이나 폰트 엔진 같은 일부 분야에서 제한적으로 쓰였다. ㄲㄲㄲㄲㄲ

그러다가 펜티엄이 돼서야 부동소수점 명령이 CPU에 기본 내장되고 지원되게 됐다. 그랬는데 그 펜티엄에서 바로 FDIV 나눗셈 결함이 발견되기는 했지만.. 가정용 컴에서까지 걱정해야 할 무슨 심각한 보안 문제 급은 아니었다. 아주 극단적으로 크거나 작은 수를 다룰 때 아주 미세하게 발생하는 문제이기 때문에.

80비트 long double의 경우, x87 프로세서에서도 지원 자체는 한다. 심지어 더 작은 32/64비트 부동소수점을 다룰 때도 중간 계산 결과는 다 80비트로 취급하기도 한다. 그러나 x87 이후에 도입된 SIMD 명령은 80비트 부동소수점을 지원하지 않기 때문에 80비트가 사실상 봉인돼 버렸다.

이거 무슨 분당선 전철이 훗날 8량 편성으로 고정되면서 처음에 미리 만들어졌던 수서-오리의 10량 기준 승강장의 일부 영역이 봉인된 것과 비슷한 것과 비슷한 느낌이다.;; ㅋㅋㅋㅋㅋ
하물며 128이나 256비트짜리 초대형 부동소수점은 어디 쓰이는 곳이 있기는 한지 잘 모르겠다.

본인이 과거에 만들었던 프로그램 중에 부동소수점 연산을 많이 하는 축에 드는 놈으로는 "3차원 그래픽 시연 프로그램"이 있다. 빌드된 실행 파일을 들여다보면 x87 명령이 많이 쓰인 게 눈에 띄었다.
그런데 얘를 컴파일러를 업글해서 다시 빌드하니 코드의 레이아웃이 싹 바뀌었다. x87의 구닥다리 fmul fld fadd fstp 대신, addsd movaps mulsd 처럼 SIMD 명령이 쓰인 것이다.

얘는 부동소수점 한둘의 연산을 넘어, 벡터· 행렬 같은 여러 데이터의 연산을 한 명령으로 한꺼번에 처리해 주는 확장 명령이다. 1999년, 펜티엄 III에서 도입됐다.
이미 Visual C++ 200x 시절부터 이 명령을 사용해서 컴파일하는 옵션이 /arch에 딸려 있긴 했다. 그러다가 2012부터는 별다른 옵션이 없으면 이 명령 세트를 사용하는 게 디폴트가 됐다~!!

이게 예전 198~90년대에 x87 명령 사용 여부와 비슷한 컴파일 옵션인 셈이다. 2012에서는 Windows XP 지원도 공식적으로는 최초로 끊겼는데 참 많은 변화가 있었다.

이상이다. 부동소수점과 관련하여 할 말한 얘기가 생각보다 많았다. ^^
x87에는 사칙연산뿐만 아니라 제곱근, 삼각함수, 2를 밑으로 하는 지수와 로그 같은 간단한 초월함수까지 CPU 명령 하나로 해치워 준다. 그러나 그렇다고 모든 수학 함수를 지원하는 건 아니어서 e를 밑으로 하는 지수와 로그는 지원하지 않는다. 2는 지원하고 e는 지원하지 않는다니.. 진짜로 수학 대신 컴퓨터 지향적인듯. ㅎㅎ

그러니 CPU빨이 없는 수학 함수는 C 라이브러리에서 어떻게 구현돼 있을까..?? 궁금해진다.
그리고 부동소수점을 10진법 문자열로 변환하거나 vice versa하는 것 말이다. 이거 은근히 어렵고 번거로울 텐데? exponent와 mantissa를 다 진법 변환하면서 두벌일을 해야 하니까..
에니악 같은 초창기 컴퓨터가 그 비효율 삽질에도 불구하고 숫자를 처음부터 10진법 단위로 묶어서 표현한 이유도 이와 무관하지 않았지 싶다.

여담: 숫자 자체를 컴퓨터가 primitive로 지원하는 숫자 unit들 여러 개를 묶어서 complex type처럼 취급하는 분야는 다음과 같다.

• 수십~수백 자리 어마어마하게 큰 정수: 공개(비대칭) 키 암호화 라이브러리에서 필요하다. 금융 거래 같은 데서..;; 얘만 기막히게 빠르게 처리해 주는 정수 연산 라이브러리도 있다.
• 유리수: 부동소수점 단독으로는 유리수 하나도 정확하게 표현이 안 되니 정수 2개 분자/분모를 따로 취급한다. Windows 계산기가 내부적으로 이렇게 동작한다고 알려져 있다.
• 복소수: 부동소수점 2개를 묶어서 실수/허수를 표현한다. 수학· 과학 일부 분야에서 쓰인다. C++에 complex라는 클래스가 있는데, 템플릿 형태여서 정수만으로 구성된 복소수도 만들 수는 있다.
• 소수점만 임의의 자리수로: 전용 수학 패키지에서 쓰인다.
• 행렬· 벡터, 사원수: 더 이상의 자세한 설명은 생략한다. 게임을 포함해 컴퓨터그래픽 분야에서 쓰인다.

Posted by 사무엘

1. 자동차 배터리와 컴퓨터 스택 메모리

자동차의 배터리 방전과 컴퓨터 프로그램의 스택 오버플로는 서로 완전히 다른 분야이긴 하지만 공돌이의 심상 면에서 공통점이 느껴지는 것도 좀 있는 것 같다.
지난 수십 년 동안 자동차는 엔진 효율이 크게 향상됐고 컴퓨터의 메모리도 동적 힙(heap)이야 넘사벽 급으로 용량이 뻥튀기 됐지만, 저것들은 용량이 획기적으로 크게 올라간 적이 없다. (특별히 그럴 필요가 없어서..)

그리고 저 둘은 남은 용량이나 고갈 징후를 미리 알려 주는 메커니즘도 딱히 존재하지 않는다.
자동차의 황산-납 배터리는 스마트폰이나 노트북의 리튬이온 배터리처럼 용량이 몇 % 남았다고 알려주는 기능이 없다. 블랙박스도 배터리의 전력 용량이 감소하면서 전압도 같이 감소하는 걸 감지해서 간접적으로 꺼진다거나 할 뿐이다.

컴퓨터 프로그램의 스택 메모리도 지역변수의 주소를 이용해서 남은 용량을 아주 간접적으로 유추할 수 있고, 시스템 exception을 이용해서 일이 벌어졌을 때 스택 overflow를 감지할 수도 있다. 하지만 이식성 있는 일반적인 방법은 존재하지 않는다. 그걸 일일이 체크하는 건 아주 비효율적이다. 이런 식으로 유사점이 있다.

2. TLS 슬롯

메모리와 관련하여 이렇게 아기자기하게 제약이 될 수 있는 게 본인이 보기엔 TLS 슬롯 공간이다.
사실, 한 사람이 만드는 프로그램이 수십~수백 종류의 코드가 동시에 실행되는 프로그램을 만들 일은 극히 드물겠지만, 문제는 내가 만들지 않은 프로그램(특히 DLL)들이 한 프로세스에 왕창 붙어서 실행될 때이다. 이런 코드들이 전부 TLS 슬롯을 하나씩만 요청하더라도 TLS 공간은 수십~수백 개씩 소모될 수 있다.

Windows 95 내지 NT 3.x시절에는 현실적으로 필요한 양과 그 당시 컴퓨터들의 평균적인 사양을 감안해서 스레드마다 TLS 슬롯이 64개씩 배당되었다. 이게 바로 TLS_MINIMUM_AVAILABLE라는 상수값의 의미이다. 역대 win32 환경 중에 TLS 슬롯이 제일 적었던 구현체가 제공했던 최소 개수가 64라는 뜻이다.

세월이 흐를수록 기본 제공되는 TLS 슬롯 수는 점차 늘어나서 Windows XP/2000부터는 64에다가 1024가 더해진 1088개라고 한다. 후대의 운영체제에서 슬롯 수가 이것보다 더 늘어났다는 얘기는 본인은 들어 보지 못했다. 힙 메모리처럼 엿가락처럼 한없이 더 늘어나야 할 필요는 없는 물건이기 때문이다.

스레드 단위로 전역적으로 공유돼야 하는 데이터가 많이 있거나 그 데이터의 길이가 들쭉날쭉 변한다면 별도의 heap 메모리를 할당하고 TLS 슬롯에다가는 포인터만 저장해야 한다. 즉, 응용 프로그램은 언제나 고정된 개수만의 슬롯을 사용하고, 슬롯 사용량을 최소화해야 한다.

내가 보기에 TLS가 꼭 필요한 때 중 하나는 사용하는 라이브러리가 너무 구닥다리여서 콜백 함수에 context 데이터를 넘겨주는 게 없어서 context 정보를 오로지 전역변수에 의지해야 할 때(+ 그런데 thread-safety가 보장돼야 할 때) 정도이다.
한 프로그램이 스레드 10개로 동작하건 100개로 동작하건 그건 소모되는 TLS 슬롯 개수와는 전혀 무관하다. 이건 그냥 실행되는 코드의 종류하고만 관계가 있다.

3. 복합 스레드 동기화

조금 부끄러운 얘기를 하자면.. 본인은 오래 전 학교의 컴공 운영체제 시간에 졸았는지, 아니면 다른 변고가 있었는지는 모르겠지만 나만의 스레드 동기화 오브젝트를 새로 만든다는 개념 내지 필요성을 지금까지 별로 이해하지 못했다. 그냥 운영체제가 제공하는 critical section이나 뮤텍스, 세마포어만 쓰면 끝이지 않은가..?? 그랬는데 회사 코드를 들여다보면서 뒤늦게야 '아...!!' 현타 비스무리한 걸 경험하게 됐다.

평범한 데이터 컨테이너가 멀티스레드 동작에 대비하여 곳곳에 뮤텍스 기반의 lock이 걸려 있는데.. 데이터를 건드리는 set쪽뿐만 아니라 단순히 read만 하는 get 메소드들까지도 내부가 전부 동일한 lock이 일일이 걸려 있었다. 흠, 이건 read일 뿐인데 여러 스레드가 동시에 접근해도 상관없지 않나? 저건 불필요한 삽질 오버헤드 아닌가? 이 lock은 빼 버려도 되겠는데?

그런데 알고 보니 그 생각은 절반만 맞았다. reader만 있을 때는 여러 스레드들이 동시에 접근해도 괜찮지만, 한 스레드라도 write를 할 때는 다른 writer는 물론이고 reader들도 다 줄 서서 기다려야 하기 때문이다. 그러니 get 함수도 lock이 전혀 없어서는 안 된다.

하지만 이렇게 정말 간단하고 범용적인 원리대로 lock의 종류를 구분하는 것이 운영체제 API로는 의외로 직통 구현돼 있지 않았다. 기존 동기화 오브젝트를 조합해서 사용자가 직접 구현해도 되며, 이런 복합 동기화는 읽기/쓰기 중 한쪽으로만 CPU가 너무 쏠리고 있을 때 분배를 어떻게 할지 같은 정책이 일방적으로 획일화 가능하지 않기 때문이다.

그래도 C++ 라이브러리의 스레드/동기화 클래스 중에는 이런 "다수 reader/단일 writer" 동기화를 구현한 놈이 혹시 있는지 모르겠다. 이런 클래스는 그냥 lock와 unlock만 있는 게 아니라 lock이 lockForRead와 lockForWrite로 세분화된다.

이렇게 custom 동기화 오브젝트를 만들면 기존 운영체제 API만으로는 바로 구현 가능하지 않은 복합 동기화를 시전할 수 있다. reader와 writer가 여러 놈이 동시에 경합할 때, 그리고 read와 write의 소요 시간이 차이가 많이 날 때 어떤 원칙으로 CPU를 배분할지 같은 세부 원칙도 손수 정할 수 있다.

그리고 디버그 빌드에서는 각종 참고 정보를 알려주고 오류를 검출하는 기능도 넣을 수 있다. 현재 포커스를 잡은 스레드, 또는 대기 중인 스레드들을 얻어 온다거나..
lock을 건 스레드가 아직 실행 중인데 그 동기화 오브젝트가 소멸되는 건 잘못된 상황이므로 곧장 예외나 assertion failure를 날린다.

(이 글을 쓰고 나서 나중에 알게 된 사실: Windows Vista에서부터 Slim Reader/Writer (SRW) Lock이라는 게 도입됐다. 크리티컬 섹션처럼 동일 프로세스 안에서만 사용 가능한 대신.. reader lock과 writer lock을 구분해서 요청 가능한 작고 가벼운 동기화 오브젝트이다. 역시 범용성이 있으니 2000년대 이후에야 도입됐구나 싶다.)

그리고 디버깅에 제일 도움이 되는 정보는.. 아무래도 deadlock 감지일 것이다.
응답이 멎은 프로그램을 강제로 break시킨 뒤, 스레드들의 스택 상태를 추적하다 보면 memory leak보다는 쉽게 찾을 수 있겠지만 크고 복잡하고 스레드를 왕창 많이 만드는 프로그램에서 이런 걸 프로그램이 디버그 정보를 통해 자동으로 찾아주면 디버깅에 큰 도움이 될 것이다. 물론 이 경우, 동기화 오브젝트가 락에 진입한 스레드들의 실행 정보를 일일이 관리하고 있어야 할 것이다.

Posted by 사무엘

1. 자연어 처리

우리나라 헌법 전문은 무진장 길고 복잡한 만연체인데, 결국 핵심은 "대한국민은 헌법을 개정한다"이다. ㄲㄲㄲㄲㄲㄲ
자, 문장 구조를 파악하기 위해 프로그램 코드처럼 들여쓰기를 적용해 주면 얼추 다음과 같다.

다만, 이런 요지의 문장 자체는 제헌헌법 시절부터 있었다고 한다. 따지고 보면 국민 교육 헌장이 기존 헌법 전문으로부터 영향을 받은 것이다.

2. AI

Posted by 사무엘

컴퓨터의 정보 기억장치는 다음과 같은 속성에 따라 분류 가능하다.

(1) 배열처럼 아무 지점이나 O(1) 시간 복잡도로 즉시 접근 가능한가? 아니면 링크드 리스트처럼 순차적으로만 접근 가능한가?
Random Access memory라는 건.. 아무렇게나 읽고 쓰기가 가능하다는 뜻이 아니라, 임의 지점 접근이 가능하다는 뜻이다.
물론 오늘날은 테이프 같은 극단적인 물건 말고는 RAM이 당연시되고 있다. 테이프는 임의 접근이 안 되니 번거로운 감기 기능이 필요했지만.. CD는 아무 트랙이나 바로 갈 수 있다.

(2) 읽고 쓰기 가능한가, 아니면 읽기 전용인가?
ROM이라고 불리는 물건들은 RAM의 속성을 지니면서 동시에 ROM인 셈이다. ROM은 RAM의 엄밀한 반의어가 아니니 유의할 것.
CD 같은 광학 디스크는 요즘 기술로 '쓰기' 자체는 가능하다. 하지만 아무 부작용이나 부담 없이 자유자재로 아무렇게나 쓸 수 있는 건 아니다.

(3) 휘발성인가, 비휘발성인가
아주 중요한 속성이다. 전원이 끊어지면 내용이 싹 다 날아가느냐, 아니면 그 뒤에도 내용이 남아 있느냐? 읽기 전용 메모리는 당연히 비휘발성이어야 할 테니 이건 읽쓰 겸용 메모리가 대상이다.
반도체 기반의 주메모리는 속도가 빠른 대신 전자이고, 나머지 보조 기억장치들은 느린 대신 용량 많고 후자의 속성을 지닌다.

(4) 매체와 reader/writer가 쉽게 분리 가능한가? 아니면 붙박이인가?
이거 무슨 철도 차량으로 치면 기관차-객차 vs 동차 같은 차이점 같다.

(5) 그리고.. 어떤 기술 배경에 따라 만들어졌는가?
다음과 같이 세 계열로 나뉜다.

1. 자기장: 테이프, 디스켓 // 디스크, 드럼.

매체 분리형에서는 테이프만이 무슨 방송국이나 데이터센터 급의 백업/아카이빙 용도로 쓰이고 있고 나머지는 도태했다. 디스켓이고 zip드라이브고 뭐고 다 망했으니까. 붙박이형은 디스크만이 '하드'의 형태로 남고 다 도태했다.
1950년대에 슈퍼컴퓨터 용으로 무려 5MB짜리 하드디스크를 지게차에다 조심스럽게 실어 나르던 시절을 보면 참 격세지감의 극치가 따로 없다.

여기는 전통적인 트랙이니 섹터니 하는 구조 구분과 '포맷'이라는 게 통용되는 기억장치이다. 하드디스크는 실린더라는 것도 있었고 말이다.
똑같은 디스켓이라도 운영체제에서 소프트웨어적으로 공간 구획을 구분하고 인식하는 방법이 다르다. 과거에는 플랫폼과 운영체제에 따라 이런 파편화가 더 심했기 때문에 디스켓들이 포맷되지 않은 채로 판매되곤 했다. 물론 IBM PC와 MS-DOS가 천하를 평정한 뒤부터는 디스켓들이 다 미리 포맷되어서 나오기 시작했다.

하드디스크는 전원이 끊어질 때 안전을 위해 파킹이라는-_- 마무리 동작도 권장되곤 했다. 물론 훗날 자동 파킹이 지원되면서 별도의 파킹 유틸리티는 화면 보호기만큼이나 별 필요 없는 눈요기 잉여로 전락했다.

2. 반도체: USB 스틱, SD카드 // SSD

메모리 반도체는 100% 전자식으로만 동작하는 물건이다. 빠른 대신에 비싸고, 무엇보다도 그 특성상 전기가 끊어지면 내용도 다 날아가는 '휘발성 메모리' 전용이었는데.. 기술의 발달로 보조 기억장치 역할도 가능한 메모리 반도체가 등장했다.
얘 덕분에 기존의 테이프나 디스켓이 완전히 전멸해 버렸다. 그리고 SSD도 가격 내려가고 용량 올라가면서 기존 기계식 하드디스크의 입지를 상당수 위협하고 있다.

SSD는 조각 모음이 필요하지 않으며, 동작하는 특성이 기존 디스크와는 많이 다르다.
USB 스틱은 매체와 구동부가 일체형인 반면, SD카드는 매체와 구동부가 분리돼 있다. (별도의 reader가 필요)
옛날 8비트 시절에 게임용으로 쓰였던 롬팩 카트리지도 1번이 아니라 2번 반도체 기반이었던 거지..??

전자기기에서 캐퍼시터(축전기)와 본격적인 화학 전지의 관계가 반도체 메모리와 타 보조 기억장치의 관계하고 비슷해 보인다~!!
전자는 충전· 방전이 아주 빠르고 용량이 아주 작으니까. 그리고 캐퍼시터를 용량을 왕창 키워서 배터리처럼 사용하려는 연구가 진행 중이기도 하다.

3. 광학(레이저)

얄팍하고 비까번쩍 빛나고 뭔가 하이테크스럽게 생긴 원반이다. 1990년대에 첫 등장했을 때는 얼마나 간지 뽀대 났겠는가.

얘는 그 특성상 붙박이라는 게 존재하지 않고 드라이버와 매체가 분리돼 있다. 기억장치들 중 디지털 방식의 음반· 영상매체와 가장 친화적이라는 특징도 있다. (그 반면, 테이프는 '아날로그' 방식의 매체..)
얘는 '쓰기'와는 그렇게 친화적이지 않다. 디스크에다가 작정하고 새로 기록 추가만 가능하며, 한번 새겨 버린 내용을 자유자재로 덮어쓸 수 없다. 평범한 디스크 저장이 아니라 종이에다 인쇄하는 것과 얼추 비슷하다고 생각해야 한다.

디스크의 영어 스펠링은 disk와 disc가 혼용되는 듯한데.. disc는 특별히 대놓고 원반 모양인 광학 매체에 한정되어 쓰이는 것 같다. 가령, 하드는 hard disk이지만, CD는 compact disc이다.
그리고 CD(+ DVD, 블루레이)는 지름이 12cm인 반면, 과거에 있었던 레이저 디스크는 지름이 12인치였다는 아주 흥미로운 차이점이 있다. 뭐, 거기에다 미니CD라고 지름 8cm짜리 규격도 있긴 하고 말이다.

한때 광학 기억장치는 용량이 방대하다는 장점이 있었지만 오늘날은 빛 바랜 장점이다. 이제는 컴퓨터에서 광학 드라이브 자체가 거의 퇴출되었고, 운영체제 설치도 그냥 네트워크나 USB로 다 되는 세상이 됐다.
그래서 DVD의 다음 규격인 블루레이는 용량이 더 방대함에도 불구하고 오늘날 존재감이 매우 미미하다. 블루레이에다가 수십 GB짜리 패키지 게임을 담아서 판매하는 시대도 아니니 말이다.

옛날에는 뭔가 레이저를 사용하는 컴퓨터 주변기기는 가격이 억소리 나게 비쌌던 걸로 악명 높았다. 레이저 프린터, 그리고 씨디 라이터.. 그게 어쩌다가 가격이 확 떨어지고 개인용 컴퓨터에 씨디를 굽는 기능까지 내장되어 들어갔는지.. 경이롭기 그지없다.
기껏 들어갔던 기능이 이제는 필요 없어져서 퇴출되는 지경이고..

※ 여담 1: 옛날 추억 더

• 1990년대에 VGA 이후로 SVGA 그래픽 카드들이 표준 규격 없이 난립했던 것처럼.. 확장 디스켓도 표준 규격 없이 너무 난립했던 것 같다. 더구나 USB니 plug & play니 없던 시절에는 하드나 디스크 드라이브를 하나 더 장착하는 것도 엄청나게 어렵고 컴퓨터 하드웨어 지식이 많이 필요하던 과업이었다. 그러니 그런 싸제 물건들이 성공적으로 보급되기가 어려웠다.
  
  
• 그나저나 이 바닥은 자동차 브레이크 말고도 '디스크와 드럼'을 쌍으로 구경할 수 있는 또 다른 분야인 게 신기하다. '자기 드럼'은 어떤 형태로 동작하는 물건이었을까..?? 개인적으로 무척 궁금하다.
  
  
• 옛날에는 테이프나 디스크에 물리적인 쓰기 방지 탭이나 딱지 같은 게 붙어 있기도 했지만.. 요즘은 그런 관행을 찾을 수 없다. (운영체제 셸이 그런 데다가도 메타데이터나 썸네일 캐시 같은 걸 임의로 써 넣곤 함)
  
  
• 옛날에는 광자기 디스크라는 것도 있었던 것 같은데.. 뭐지? 1번과 3번의 하이브리드인가 싶다.

카세트 테이프(자기장)나 롬 카트리지(반도체)는 8비트의 산물이다. 16비트 IBM 호환 PC급에서 저런 것들을 취급하는 사례는 내가 아는 한 없다.
그 대신 디스켓 FDD는 컴퓨터 붙박이 형태로 16비트 이후 시대를 풍미했다가 64비트 시대에는 사실상 전멸했다.
CD-ROM은 16비트 도스 시절에도 존재하긴 했지만 mscdex니 뭐니 하는 굉장히 무거운 드라이브를 실행해야 사용 가능했다. 그리고 386, 486급 이상 PC의 전유물이었다.
그 뒤로 USB 메모리는 도스와의 유의미한 접점이 없다. ^^

아무리 생각해도 1990년대 중후반에 plug & play와 USB는.. 2000년대 중후반의 64비트와 멀티코어하고 굉장히 비슷한 관계인 것 같다.
서로 담당하는 분야는 다르지만 결국 비슷하고 관련 있는 성격의 기술이었다는 점에서 말이다.

※ 여담 2: 정보 저장이라는 관점에서 성경 본문 고찰

성경에는 뭔가 정보 기록 매체를 암시하는 얘기가 있다. 가령, 요한복음의 21장 25절 제일 마지막 구절은 이렇다.
"예수님께서 행하신 다른 일들도 많으므로 만일 그것들을 낱낱이 기록한다면 심지어 이 세상이라도 기록된 책들을 담지 못할 줄로 나는 생각하노라."

"그 크신 하나님의 사랑"이라는 찬송가의 3절 가사는 이렇다.
"하늘을 두루마리 삼고 바다를 먹물 삼아도 한없는 하나님의 사랑 다 기록할 수 없겠네"

흠, 책이 아니라 SD카드라면 어떨까? 자기 테이프라면 어떨까..??
혹시 생명책이 실제로는 책이 아니라 무슨 SQL 서버가 돌아가는 IBM 메인프레임인 건 아닐까?

Posted by 사무엘

컴퓨터 알고리즘 문제 중에는.. "N개의 원소로 구성된 목록에서 majority.. 과반/다수파라는 게 존재하는가? 존재한다면 무엇인가?"를 구하는 문제가 있다.
목록에서 과반의 원소가 다 같은 값이면 그게 바로 majority라고 정의된다. 원소들은 꼭 대소 관계가 성립할 필요가 없고 그냥 동등성 판단만 가능하면 된다. 그러니 꼭 정수가 아니어도 된다.

또한, 반반이 아니라 과반이라는 특성상, majority는 존재하지 않거나, 유일하게 존재.. 언제나 둘 중 하나이다. 공동 1위 같은 것도 고려할 필요가 없다.

이 문제는 뭐랄까.. 단순하면서도 참 므흣하다.
일단, "목록에서 가장 자주 등장하는 원소--등장 빈도수가 가장 큰 원소를 구하시오"라고 접근하지 않는 게 핵심이다.
각 원소들의 빈도수를 일일이 관리하자면 알고리즘의 시간 복잡도가 기본이 O(n^2)에서 시작할 것이고, 균형 잡는 tree 기반의 컨테이너를 사용한다 하더라도 O(n log n)이 한계이다.

그러나 이 문제를 풀기 위해서는 일을 그렇게 크게 벌일 필요가 없다.
각 원소의 빈도수가 아니라.. "이 목록은 과반의 원소가 그냥 동일한 값인가?"라고 접근하는 게 좋다.

수학인지 논리학인지 거기에는 "비둘기집의 원리"라는 게 있다. N+1개의 물건을 N개의 상자에다 다 집어넣는다면, 적어도 한 상자에는 그 물건이 2개 이상 들어가 있다. 뭔가 미적분에서 말하는 중간값 정리처럼.. 너무 당연한 말 같은데 말이다.
그것처럼 어떤 목록에 같은 원소가 "과반"이라면 그 목록은 다음 둘 중 한 특성을 반드시 갖게 된다.

• 과반의 원소가 아무리 고르게 분산되어 분포한다 하더라도, 그 원소가 연달아 두 번 이상 등장하는 구간이 반드시 하나 이상 존재한다~! 1 1 2 1 특히 원소의 전체 개수가 짝수라면 이건 뭐.. 무조건 빼박이다.
• 만약 그게 아니라면.. 그냥 맨 마지막 원소가 다수파이다.

어, 정말 저렇게 단정할 수 있나 의아할 텐데.. 이런 과감한 주장은 다수파의 정의가 절반의 '초과', '과반'이기 때문에 성립 가능하다.
절반을 포함하는 '이상'이기만 해도 위의 조건들은 당연히 성립하지 못하게 된다. "1 2 1 2" 같은 것만 생각해 봐도 알 수 있다.

이렇듯, 다수파가 존재할 때 가질 수밖에 없는 목록 전체의 특성을 생각하면.. 다수파를 굉장히 단순한 절차만으로도 정확하게 구할 수 있다.

• 최초엔 맨 첫째 원소가 다수파라고 가정하고 후보로 지정한다. 연속 등장 횟수(이하 점수)도 1을 부여한다.
• 그 다음 원소가 후보 원소와 동일하면 점수를 1 증가시킨다. 그렇지 않으면 점수를 1 감소시킨다.
• 단, 이미 현재 점수가 0이 된 상태여서 더 감소시킬 것이 없으면 후보 자체를 지금의 새 원소로 교체한다. 그리고 점수를 1로 다시 부여한다.
• 이 과정을 모든 원소들에 대해 수행한 뒤, 현재 지정되어 있는 후보를 결과값으로 되돌린다.

위키백과에는 이 과정을 다음과 같이 시각적으로 잘 묘사한 그림이 있더라.
정말 허무할 정도로 단순하다. 이 알고리즘은 고안자의 이름을 따서 Boyer-Moore majority vote algorithm이라고 명명되어 있다. 1981년에 학계에 처음으로 발표됐다고 하는데.. 동작하는 방식을 보니 후보, vote 이란 워딩이 적절해 보인다.

Boyer-Moore 이거 혹시 "문자열 검색 알고리즘에도 나오는 이름이 아닌가?"라는 생각이 들 텐데.. 정확하다. 동일한 명칭이다. ㄲㄲㄲㄲ

단, 위의 알고리즘은 목록에 다수파라는 게 실제로 존재하지 않더라도 언제나 후보를 갖고 있다가 되돌린다. 그러니 목록에 다수파가 존재한다면 정확한 답을 되돌리지만, 애초에 다수파가 존재하지 않는다면 뭔가 임의의 엉뚱한 후보를 되돌린다.

그렇기 때문에 이 알고리즘에는 2nd-pass, 즉 후처리라는 게 필요하다. 앞의 1st-pass를 통해 구해진 후보가 진짜로 다수파가 맞는지, 얘만 개수를 처음부터 다시 세어 보는 것이다.
1st-pass 때 쓰였던 점수 변수는 증가했다가 감소하기를 반복했기 때문에 정확한 개수가 담겨 있지 않다.
이거 무슨 분수· 무리방정식을 풀고 나서 검산을 해서 무연근을 제거하는 것과 비슷한 느낌이다.

자, 두 pass 모두 시간 복잡도는 O(n)이고, 공간 복잡도는 지역변수 꼴랑 한두 개.. O(1)에 지나지 않는다. 정말 놀랍지 않은가?
얘는 알고리즘 자체는 쉽게 이해할 수 있지만, 정말 이렇게만 해도 언제나 문제에 대한 정확한 답이 구해지는지 correctness를 이해하는 게 좀 빡셀 수 있는 문제이다.

알고리즘이라 하면 복잡한 기법을 동원해서 무식하게 풀었을 때 O(n^2)짜리인 것을 O(n log n)으로 낮춘다거나, 팩토리얼/지수함수 급인 것을 O(n^2)나 O(n^3)으로 낮추는 형태인 게 많다.
그러나 최적화를 통해서 이렇게 O(n)을 만들 수 있는 문제는 흔치 않아 보인다.

이 다수파 구하기와 성격이 아주 비슷한 문제는 N개의 숫자 목록 내부에서 "합이 가장 큰 연속된 구간을 찾기"인 것 같다. 당연히 양수와 음수가 뒤죽박죽 섞여 있는 목록에서 말이다.

정답이 (x~y) 구간은 그야말로 1<=x<=y<=N 아무렇게나 가능하기 때문에 이것도 언뜻 보기에는 시간 복잡도가 O(n^2)이나 최하 O(n log n)이 될 것 같다. 그러나 얘도 아주 간단한 검사만 하면서 시간 복잡도 O(n)과 공간 복잡도 O(1) 만으로 아주 빠르게 풀 수 있다.

• 정답 구간이 맨 첫 원소에서 시작된다고 가정하고 각 원소들을 쭉쭉 더해 본다. 그 합이 지금까지 구한 max보다 더 크면 최대값을 갱신하고 정답 구간도 업데이트 한다.
• 그런데 그러다가 합이 음수가 돼 버리면... 그러면 지금까지 살펴봤던 구간은 "더 살펴볼 필요가 없고" 그냥 통째로, 아무 미련 없이 버리면 된다. 그 다음에 양수가 나오는 구간부터 시작점을 새로 설정하고 동일한 과정을 반복한다.

더 살펴볼 필요가 없기 때문에 시간 복잡도 O(n)이 가능한 것이다. 이게 아까 다수파 문제에서 점수가 음수가 돼 버린 시점에서 후보를 깔끔하게 바꿔 버리는 것과 비슷하다. 왜 이렇게 해도 되는지를 생각하는 게 이 문제의 관건이다.

Posted by 사무엘

1.
고층 건물에는 엘리베이터가 있다.
그런데 건물이 왕창 크고 층이 수십 개 이상으로 많고, 이용하는 사람도 왕창 많으면.. 엘리베이터도 한 대만으로는 감당이 안 되니 여러 대를 설치하게 된다.

그런데 이게 설치만 한다고 장땡이 아니다. 엘리베이터는 에스컬레이터나 다른 정규 노선 대중교통과 달리, 승객의 수요예 따라 그때 그때 이동하는 물건이다. 이 점에서는 버스보다는 택시에 더 가까운데, 그래도 중간 합승이 허용된다는 차이가 있을 뿐이다.
이런 특성상, 엘리베이터는 승객과 차량을 똑똑하게 분배하는 운영 시스템이 필요하다. 무식하게 운용하면 차량이 많아도 승객들은 엄청 오래 기다려야 하고, 탄 뒤에도 층마다 서면서 엄청난 비효율이 발생하기 십상이다.

그래서 엘리베이터를 똑똑하게 분배하는 시스템이 없던 과거부터 현재까지 제일 보편적으로 쓰이고 있는 단순한 방법은 (1) 각 차량의 용도를 그냥 층별로 물리적으로 분할하는 것이다. 저층부/고층부, 그리고 홀/짝 이렇게 말이다.
이건.. 모든 엘리베이터들이 바쁠 때야 그럭저럭 괜찮은 방법이다. 그러나 서로 다른 구간끼리 오가는 사람은 불편하게 환승을 하거나 인접층으로 이동해야 한다. 그리고 엘리베이터들이 전혀 바쁘지 않은데도 나와 더 가까이 있는 엘리베이터를 이용하지 못하고 먼 쪽의 엘리베이터를 강제로 이용해야 하는 비효율이 발생한다.

얘보다 약간 더 발전된 엘리베이터는.. 버튼을 누르면 그 층의 모든 엘리베이터의 버튼에 불이 켜진다. 그리고 (2) 지금 층에서 가장 가까이 있는 엘리베이터를 중앙 시스템이 알아서 골라서 보내 준다.
고급 호텔 같은 곳의 엘리베이터가 이런 형태인 경우가 있다. 각 엘리베이터들이 현재 몇 층에 있는지 표시도 해 주지 않는다. 그리고 더 신기한 건.. 밖에서 상행이나 하행 중 한 버튼을 누르는 게 아니라, 처음부터 가고 싶은 층을 찍게 돼 있는 것도 있다.

요런 엘리베이터는 어느 엘리베이터의 문이 열릴지 알 수 없어서 승객이 처음에 약간 헤맬 수 있지만, 그래도 물리적인 층 분담보다는 더 똑똑하고 효율적으로 동작할 가능성이 있다.
하지만 약간 아쉬운 점은.. 중앙 시스템이 찜한 엘리베이터가 승객의 층으로 오는 도중에 다른 승객 때문에 많이 지체되고 있을 때, 그냥 다른 엘리베이터를 대신 지정하는 게 안 될 확률이 높다는 것이다. AI가 그런 것까지 고려해서 만들어지지는 않기 때문이다.

이건 절대적인 정답이 없는 문제이다. (1) 엘리베이터를 이미 탄 승객, (2) 밖에서 기다리는 승객, 그리고 (3) 엘리베이터 자체의 주행 거리 총량(소모 전력) 사이의 trade-off 제로썸 게임이기 때문이다.

그래도 최적해에 근접하는 가장 효율적인 전략은.. (1) 엘베들이 바쁘지 않을 때는 층수 구분 따위 불문하고 가장 가까이 있는 차량을 보내 주고, (2) 도중 정차도 일단은 아무 요청이나 들어 주되, 이 방향으로 가는 동안 2번, 3번 이상 이미 정차를 했다면 그때부터는 요청을 서서히 안 들어 주고 다른 차량을 대신 보내는 식으로 유도리를 발휘하는 게 좋을 것 같다.
횟수 제한, 또는 앞으로 최소한 n층 정도는 무정차로 진행.. 이런 식으로 정차를 제한할 수 있다.

물론 대체 차량이 너무 멀리 떨어져 있다거나 하면 전략이 달라지게 된다.
그리고 처음에 찜했던 차량이 너무 오랫동안 '열림'으로 붙잡혀서 못 가고 있을 때도 가까이 있는 다른 차량을 대신 보내 줘야 한다.

이 정도면 거의 AI 기술까지 접목해도 되지 않나 싶다.;;
AI가 진짜 똑똑하게 동작하려면 승객을 목적지 층별로 분할하는 것까지 알아서 처리할 필요가 있다. 차량들을 강제로 홀/짝, 고/저로 구분하지 않더라도 말이다. 모든 차량에 모든 층 승객이 고르게 뒤섞여 있으면 AI 할아버지라 해도 효율이 떨어지는 걸 피하기 어렵기 때문이다.

그리고 그렇게 하기 위해서는 엘리베이터를 기다릴 때 가고 싶은 층을 미리 지정할 필요가 있다. 그러면 이 AI가 상황을 대충 파악하고는 "3층, 7층, 12층 가실 승객은 지금 오는 엘리베이터 B차량을 타십시오. 4층, 10층, 15층에 가실 승객은 1분쯤 뒤에 도착 예상되는 저쪽 A차량을 타십시오" 이렇게 구간을 적절하게 나눠서 교통정리를 할 수 있다.
물론, 다음 엘리베이터의 도착이 너무 늦어지고 있으면 한 엘리베이터가 좀 더 촘촘하게 정차하게 된다. 이걸 유동적으로 결정하는 것도 AI의 몫이다.

이렇듯, 엘리베이터 분배도 깊고 어렵게 생각하면 끝이 없는 문제라는 걸 알 수 있다.;; 실용성도 아주 높고 말이다. 오죽했으면 엘베 관제는 1989년 제1회 국제 정보 올림피아드의 문제로 나오기도 했다.
층수가 20? 30? 정도 넘어가면 주행 속도도 굉장히 빨라져서 도착하기 수 층 전부터 감속하는 게 느껴지는 고속 엘리베이터가 투입되는 듯한데.. 이런 건 본인도 태어나서 지금까지 경험한 게 극소수이다. 엘베가 다 같은 엘베가 아닌 듯하다.
딱 층에 맞게 정차하는 건 지하철 전동차가 역의 정차 위치에 정확하게 맞춰서 정지하는 것과 비슷한 테크닉이라 하겠다.

2.
고층 건물에서 다수의 엘리베이터를 분배하는 알고리즘은 자동차를 통제하는 신호 알고리즘과도 비슷한 구석이 있다.
특히, 도로 상황을 전혀 고려하지 않고 그냥 무조건 일정 간격으로 적록 신호를 주는 게 엘베로 치면 무식하게 홀/짝, 고/저를 나눈 것과 비슷하다.

모든 방향에서 차들이 엄청 많이 다닐 때는 묻지도 따지지도 말고 그렇게만 해도 충분히 공평하다. 그러나 차량 통행이 아주 적을 때도 그렇게 하면 쓸데없는 대기 시간이 길어져서 비효율적이고 불편하다.
그래서 작은 도로에서는 평소에는 적록 신호이다가 심야에는 황색 점멸로 신호가 바뀌어서 일말의 스마트함을 추구하기는 하는데.. 신호 종류가 바뀌는 기준은 그냥 밤 11시에서 아침 6시 사이처럼 미리 지정된, '하드코딩'된 시간대일 뿐인 게 좀 아쉽다.

그러니 미래에는 신호라는 것도 더 스마트하게 바뀌어야 하리라 생각된다. 아까 그 엘리베이터 분배 알고리즘에서 하던 고민이 그대로 적용된다. 트래픽이 많을 때와 적을 때의 전략이 서로 크게 달라지는데, 그 경계 판단을 잘 해야 한다.
그래서 운전자가 시험 든다거나 분노해서 신호를 위반하려는 충동을 느끼지 않게 해야 한다. (1) 다니는 차가 아무도 없는데 빨간불이어서 쓸데없이 멀뚱멀뚱 서 있는 것, 그리고 (2) "왜 나만 갖고 그래~ 왜 교차로마다 계속 신호에 걸리는 거야..?? 이런 걸 아주 없애지는 못하더라도 최소화해야 할 것이다.

좌회전을 위해서 비보호나 점멸 대신 감응 신호가 더 늘어나고, 교차로 건너편이 계속 막히고 있으면 애초에 파란불이 되지 않게 신호등이 더 똑똑해져야 할 것이다.
비보호를 대체하는 좌회전 감응 신호는 좌회전 차량이 요청하자마자 무작정 맞은편 방향을 틀어막는 게 아니다. 처음 20~30초 정도 동안은 맞은편에 차가 없어서 충분히 안전할 때만 파란불 신호를 준다. 그렇지 않고 너무 오랫동안 좌회전을 못 하고 있으면 그때에야 불가피하게 맞은편 방향을 막고 파란불 신호를 준다.

이전글에서 언급했던 것처럼 교차로 건너편에 차가 들어갈 자리가 없으면 우리 신호가 돌아왔더라도 파란불 신호를 주지 않는 것도 덤.. 꼬리물기도 원천 차단된다.
이런 스마트 신호 체계 하에서는 교통법규 위반 건수가 줄어들고 교통사고도 자연히 더 줄어들 것이다.

Posted by 사무엘

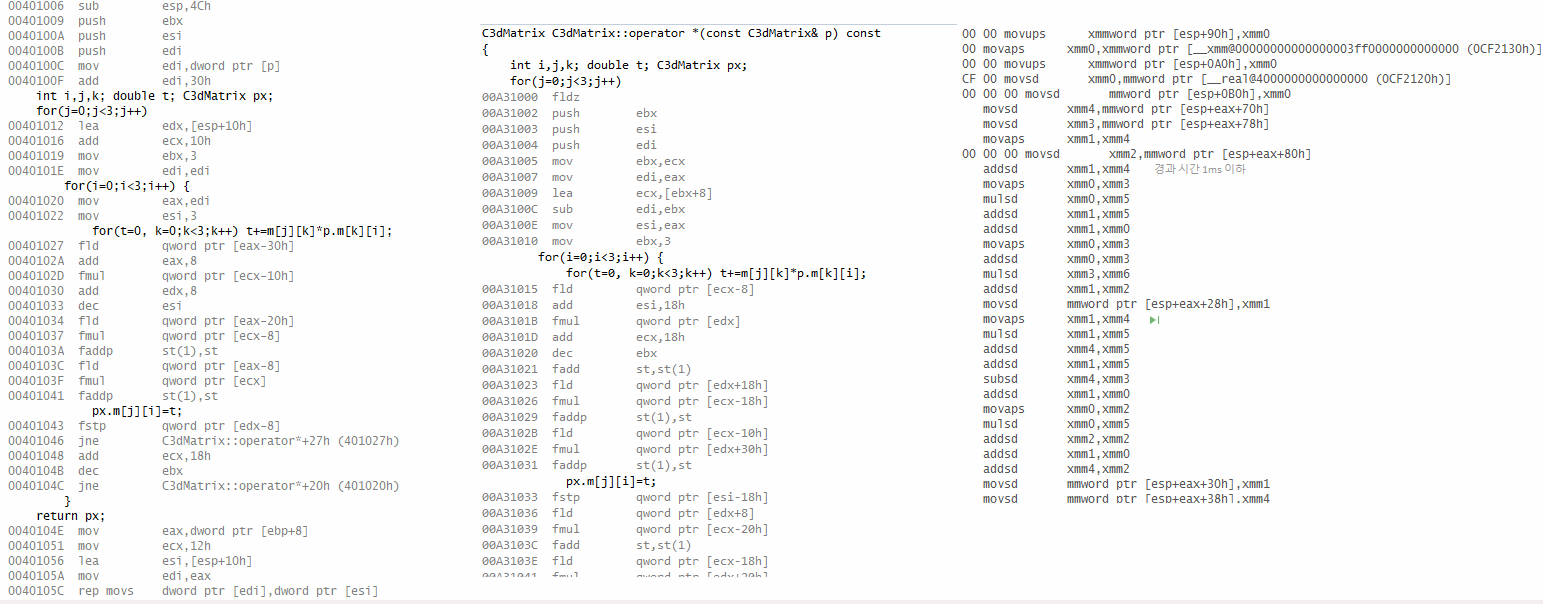
1. 성능과 알고리즘

(1) 현실의 퀵 정렬 알고리즘 구현체는 구간의 크기가 일정 기준 이하로 작아지면 그냥 O(n^2) 복잡도의 단순한 삽입 정렬로 대체하곤 한다. 그게 더 효율적이기 때문이다.

(2) 균형 잡힌 트리는 삽입, 탐색, 삭제가 모두 O(log n)의 복잡도로 되는 매우 유용한 자료구조이다. 그렇기 때문에 단순히 메모리 레벨의 set이나 map 컨테이너뿐만 아니라 파일 시스템이나 DB 같은 디스크 레벨에서도 쓰인다.
요즘 아무렇게나 DIR을 해도 파일 목록이 언제나 ABC 순으로 정렬되어 출력되는 이유는.. NTFS 파일 시스템이 내부적으로 이런 트리 구조를 사용하기 때문이다. (반면, 과거의 재래식 FAT는 연결 리스트 기반이어서 파일 목록의 정렬이 보장되지 않음)

단, 디스크 레벨에서는 단순한 이진 나무가 아니라, 이를 변형하여 한 노드에 딸린 자식이 좀 더 많은 B+ 같은 트리 구조가 쓰인다. 왜냐하면 디스크는 메모리보다 입출력 속도가 훨씬 더 느리며 랜덤 지점 탐색에 취약하기 때문이다.
그래서 한 노드 안에서 선형 검색을 좀 더 하더라도, 노드 하나를 탐색하고 읽는 횟수를 줄이는 게 더 이득이다. 다만, 이런 이념도 재래식 하드디스크가 아니라 플래시 메모리에서는 유효하지 않을 수 있다.

(3) 한 번에 한 스레드만 접근 가능해야 하는 코드가 있다면 보통 그 구간을 critical section이나 뮤텍스 따위로 둘러싼다.
그런데 이것도 "어? 다른 스레드가 이미 들어가 있네? 그럼 우리는 닥치고 바로 대기".. 이렇게 단순무식하게 하는 것보다,
loop을 돌면서 busy waiting, polling, spin lock을 n번만 더 시도해 보고 "그래도 여전히 다른 스레드가 나가지 않았으면 그때 대기 타자" 이런 유도리 전략이 좀 더 효율적일 때가 있다.

왜? 대기를 탔다가 깨어나는 작업 자체가 사용자 모드에서 커널 모드로 들어갔다가 나오는 것이며, 수천 사이클에 달하는 CPU 오버헤드를 요구하기 때문이다. 대기하고 있는 스레드는 CPU를 먹지 않지만, 대기 상태로 들어가거나 깨어나는 출입 과정은 공짜가 아닌 것이다.

더구나 요즘 컴퓨터는 코어가 여럿 있기 때문에 한 스레드에서 아주 잠깐 무식한 busy waiting을 하더라도 그게 타 스레드의 실행 성능에 영향을 주지 않는다. 그럴수록 대기 진입을 한 템포 늦춰서 신중하게 하는 게 가성비가 더 커진다.

일상 생활에다 비유하자면, 여러 잡다한 물건을 들고 있어서 무거운 채로 엘리베이터나 버스를 기다리는 것과 비슷하다. 이걸 바닥에 완전히 내려놓아 버렸다면 팔이 힘들지는 않지만, 그걸 다시 집어드는 것도 굉장히 번거로운 일이 된다. 그러니 버스나 엘리베이터가 수 초 안으로 금방 온다면 그냥 그 물건들을 들고 기다리고 있는 게 더 낫다.

이렇듯, 컴퓨터에서는 성능을 최대화하기 위해 한 방법만으로 만족하지 않고, 상황에 따라.. 특히 아주 제한된 문맥에서는 통상적으로 비효율적이라고 알려진 무식한 방법까지도 동원한다는 걸 알 수 있다. 스타로 치면 여러 유닛을 조합하는 것과 같다.

2. 자원의 회수

식물은 죽어서 말라 비틀어진 잎· 줄기나 썩은 열매 따위의 처리가 아주 간편한 축에 든다. 땅에 파묻기만 하면 거름이 되고 도로 자연으로 돌아가고 구성 물질이 회수된다.
뭐, 동물도 궁극적으로 그렇게 되기는 한다. 하지만 사체가 분해되는 과정이 식물보다 훨씬 더 더럽고 끔찍하고 더 오래 걸리는 편이다.

이런 물질의 순환은 뭔가.. 가상 머신에서 GC에 의해 자동 관리되는 메모리 같다는 생각이 들지 않는지?
본격적으로 물질의 메모리 누수가 문제되기 시작한 건 인류가 자연이 제대로 감당하지 못하는 플라스틱 같은 고분자 화합물을 만들어서 쓰기 시작하고부터이다. 그리고 반감기가 끔찍하게 긴 방사능 물질도 이런 범주에 든다고 볼 수 있겠다.

뭐, 썩지 않는 물질이 다 문제이고 골칫거리는 아니다. 수도관 같은 건 절대로 부식되거나 썩지 않는 재료로 만들어서 수백, 수천 년은 써야 할 테니 말이다.

3. 코드

(1) 우리나라의 모든 법조문들이 몽땅 github에 올라오고, 전체 개정 이력을 Show log 명령을 통해서 조회하고 싶다는 생각이 든다. 전철 노선도 같은 물건도 마찬가지이다.

(2) 대학교 컴터공학과 학부에서 시스템 프로그래밍 시간에 MIPS 어셈블리어 갖고 깨작깨작 실습하는 건.. 육사에서 승마나 백병전 총검술 잠깐 맛보기 하는 것과 정확하게 대응하지 싶다~ ㅋㅋㅋ
학교에서 뭔가 C/C++, Java, Python 같은 실용적인(?) 언어 말고 뭔가 비현실적인 언어를 다뤄 보는 게 이렇게 어셈블리어 같은 레거시 계열, 아니면 엄청나게 순수한 이론 이상을 추구하는 함수형 언어 계열.. 이렇게 둘로 나뉘는 듯하다.

(3) 자동차 취급설명서는 소스 코드 곳곳에 들어서 있는 조건부 컴파일의 완벽한 예시로 보인다. * 표시가 돼 있는 각종 선택사양들.. 그리고 악보의 음표 위에 붙은 각종 나타냄말? 스타카토, 스타카티시모 이런 건 매크로의 예시이다.
악보는 각종 반복과 분기가 복잡하게 꼬이면 흐름이 진짜로 어지간한 프로그램 코드처럼 바뀌기도 한다.

(4) 성경에서 '주의 책', '(어린양의) 생명책' 같은 상상 속의 거대한 책이 언급된 걸 보면.. 예수 믿는 컴터쟁이들은 하늘나라에 있는 거대한 데이터베이스와 DB 서버 정도는 떠올릴 수 있을 것 같다.
물론 인간이 만든 컴퓨터는 신의 주요 성품 중 하나인 '무한, 영원'이라는 걸 절대로 구현하지 못하는 물건이다. 그러니 DB 드립은 마치 "김 성모 스타일의 성경 이야기"만큼이나 그냥 웃자고 늘어놓는 말일 뿐이다.

(5) 요한복음의 마지막 구절인 "이 세상이라도 예수님의 행적을 기록한 책들을 다 담지 못할 것이다"는 정보량과 관련된 언급이다. 그리고 삼손의 수수께끼 놀이는 정보 보호· 보안과 관련된 통찰을 주는 이야기이다.

4. 자동과 수동

요즘 수동 변속기 차량을 몰 줄 아는 사람이 갈수록 드물어지듯, 컴터 업계도 C/C++처럼 메모리를 수동으로 관리하는 저급 언어를 제대로 다룰 줄 아는 사람이 갈수록 드물어지는 것 같다.
직장에서 부사수로 들어온 어린 신입 개발자에게 사수가 메모리 leak이라는 개념을 알려주는 게 굉장히 뜻밖이고 놀라워 보였다.

하긴, 공대 1학년의 기초 필수 프로그래밍 과목에서 가르치는 언어도 초창기엔 C/파스칼이다가 나중에 Java를 거쳐 지금은 파이썬이지 않은가. 프로그래밍을 위한 전산학적인 소양하고, C나 컴퓨터 특유의 지저분한 감각이랄까, 이 둘이 영역이 완전히 일치하지는 않기 때문이다.

고깃집의 경우, 직원이 알아서 고기를 다 썰고 구워 주는 곳은 자동 변속기-_- 같고, 손님이 직접 고기를 얹고 굽고 자르고 뒤집어야 하는 곳은 수동=_=;;에 해당된다. 후자보다는 전자가 아무래도 마음 편하게 고기를 먹을 수 있지만.. 인건비가 추가되어 고기값이 더 비쌀 것이다.

5. 전체 리셋

컴퓨터 시스템을 날리는 방법으로 sudo rm -rf 라든가=_= Windows의 레지스트리 날리기, 시스템 디렉터리 날리기 같은 게 있다.
운영체제가 아닌 DB에서는 delete * 내지 drop table 같은 파괴적인 쿼리가 있다. 손가락 까딱 잘못 건드려서 회사 재산과 관련된 DB를 날렸다간 짤리는 정도를 넘어 손해 배상 소송을 당할 수도 있을 것이다.

그런데 국가로 치면.. 헌법 제1조가 바뀌거나 날아가는 게 그런 급의 파괴적인 사건일 것이다. 헌정 체제가 쿠데타로 인해 싹 뒤집히거나, 아니면 전쟁에서 지기라도 해서 외적이 자국 행정부를 완전히 접수했을 때에나 있을 수 있는 일이다.

우리나라의 경우, 옛날에는 "대한민국은 민주공화국이다" 같은 몇몇 조항은 개헌조차 아예 영원히 불가능한 조항으로 못 박으려는 시도가 있었다. 컴퓨터로 치면 운영체제의 작동과 직접적인 관련이 있는 일부 시스템 파일을 절대 변조· 삭제할 수 없게 특수하게 보호하는 것과 비슷하다고 하겠다(업데이트 받을 때만 빼고).

하지만 법리적으로 볼 때 그렇게까지 할 필요는 없기 때문에 개헌 불가 조항 같은 건 과거의 해프닝으로 끝났다. 그리고 지금 6공화국 헌법은 그렇잖아도 개헌이 너무 어려운 형태가 된 감이 좀 있다.;; 과거에 널뛰기 하듯이 수시로 개헌하던 관행을 없애고 싶었던 심정은 이해가 가지만 지금은 그것 때문에 미래까지 발목이 잡힌 것 같다.

6. C++ export와 우주왕복선

2000년대 초에.. EDG 같은 일부 C++ 컴파일러 개발사에서는 희대의 흑역사 표준 기능이던 export를 구현하느라 상상을 초월하는 삽질을 했던 거랑,
NASA에서 2003년의 컬럼비아 우주왕복선 사고 이후에 이제는 우주왕복선을 띄울 때마다 옆에 구조용 예비 기체까지 같이 대기시키면서 정말 눈물겨운 삽질을 잠시 했던 것..
둘이 시기도 비슷하고 심상이 뭔가 묘하게 비슷하게 느껴진다.

전자는 지금까지 C++ 표준에 새로 추가되었던 복잡한 기능들과는 구현 난이도가 차원이 달랐다. 기존 언어 구조의 근간을 다 뒤엎어야 하는 헬 수준이었는데, 그렇다고 템플릿의 모듈화를 제대로 실현해 주는 것도 아니었다. 이건 정말 백해무익에 가까운 미친 짓이었다. 결국 export는 2010년대 C++11에서는 완전히 삭제되었다.

우주왕복선에다가 구조 미션까지 추가한 것 역시.. 셔틀 한 대에다가 사람을 11명이나 태우는 것(기존 승무원 7 + 구조 요원 4), 안 그래도 3대밖에 없는 셔틀을 매번 2대나 세팅해야 하는 것, 묘기에 가까운 어렵고 위험한 기동으로 조난 당한 셔틀에 접근해서 사람을 구조하는 것..
살인적인 비용 대비 사람을 살릴 가능성도 별로 없는 미친 짓이었다. 다행히 이 미션이 실전에서 쓰인 적은 없었으며, 우주왕복선 역시 C++11과 비슷한 시기인 2011년에 완전히 퇴역했다.

7. 나머지

(1) 생물은 번식할 때 동물과 식물을 막론하고 가까운 혈통끼리 교배하지 말고, 최대한 먼 촌수끼리 다양하게 섞여서 교배해야 유전병 없이 건강한 후세가 태어나고 안전하다고 여겨진다. 유전적 다양성이란 게 중요하다.
이런 걸 뭔가 숫자의 특성으로 표현하면 해시값의 충돌이 안 나는 것, 셸 정렬이 빠르게 수행되는 간격 수열을 구하는 것(무식하게 2^n에서 절반씩 줄이는 건 최악), 퀵 정렬의 pivot 중간값을 적절하게 잘 고르는 것에 대응하는 것 같다.

(2) 자동차나 자전거 운전하다가 상대방과 부딪칠 것 같아서 한쪽으로 피하는데..
골때리게도 상대방도 내가 피하는 방향과 같은 방향으로 피하고, 이 상황을 탈피하지 못해서 결국 부딪히는 경우가 있을 수 있다.
이런 게 머신러닝이나 방정식 근 찾기에다 비유하자면 처음에 시작점을 잘못 잡고 학습을 잘못 시켜서 최적해로 수렴을 못 하고 삼천포로 빠진 것과 비슷해 보이는 상황이다. 아니면 데드락을 극복하지 못했거나.;;.

(3) 옛날, 1955년쯤에 중공의 마오 주석께서는 하늘을 향해 삿대질을 하며 "저 새는 해로운 새.." 아니, "참새는 해로운 새"라고 교시하시였다는데..
1968년쯤에 네덜란드의 전산학자 다익스트라는 ACM 저널을 통해 "GOTO Considered Harmful".. 즉, 스파게티 코딩이 해롭다고 저격했었다. 오늘날은 저 두 말투가 모두 밈..처럼 쓰이고 있다. ㅋㅋㅋ

Posted by 사무엘

1. 숫자를 표현하는 방식

20세기 중반에 컴퓨터가 아직 진공관 기반으로 만들어지던 시절에는 전기식이 아닌 전자식으로 바뀐 것뿐만 아니라 10진법 대신 순수 2진법을 사용하기 시작한 게 큰 전환점으로 여겨진다. 그게 더 기계 지향적이고 직관적인 설계이기 때문이다.

이건 사람으로 치면 별도의 교육을 통해 암산 때 머릿속에서 아라비아 숫자 대신 주판알을 떠올리는 것과 비슷하지 않을까 싶다. 아라비아 숫자는 문자로서 실용적인 기능도 겸하려다 보니, 숫자의 본질과 연산에 직관적으로 대응하는 체계가 아니기 때문이다.
심지어 주판법에는 선주법과 후주법이 모두 존재한다. 이건 컴퓨터에서 big/little endianness와 거의 동일한 개념인 것 같다.

2. 색공간과 실제 공간

우리가 사는 현실의 공간은 길이· 너비· 높이라는 xyz 세 축, 즉 3차원이라고 여겨진다.
그런데 우리에게 시각을 인지시켜 주는 색이라는 것도 어떤 형태로 축을 나누든.. RGB건 HSL이건 CMY건 결국 3개의 축으로 이뤄진다는 게 시사하는 바가 커 보인다.
가령, 색에서 hue라고 불리는 빨주노초~파남보 요소는 가시광선 파장의 차이라는 1차원 축으로 변별된다. 하지만 채도(S)와 명도(L)는 또 다른 차원의 변수라는 것이다.

컴퓨터의 그래픽 카드에서는 RGB 각 축에 대해 8비트의 정보량을 부여해서 총 2^24, 1600여 만 가지 색상을 제공하곤 하는데, 정작 1픽셀의 크기는 3바이트 24비트가 아니다. 컴퓨터가 처리하기 편한 단위인 4바이트 32비트 단위를 사용하며, 나머지 남는 8비트에다가는 픽셀의 알파 채널 정보를 넣곤 한다. 이건 여러 이미지를 부드럽게 합칠 때 활용된다.

알파 채널은 색깔을 나타내는 축 자체는 아니지만 색의 표현과 관계 있는 정보이다. 이걸 포함한 pixel format을 RGBA 구조라고 한다. 하지만 Windows의 GDI API는 1980년대에 개발되었으며, 픽셀에서 상위 8비트를 팔레트 등 독자적인 다른 용도로 이미 사용하다 보니 훗날 알파 채널을 제대로 지원하지 못하는 촌극이 벌어졌다. 그 역할은 GDI+ 등 후대의 API가 계승하게 됐다.

RGBA라는 개념은 물리학에서 XYZ 공간 세 축에다가 시간을 더한 XYZT 4차원과 뭔가 비슷하게 느껴진다.;; 그것도 기하학적 의미에서 정확한 4차원을 말하는 건 아니니 말이다. 하긴, 생각해 보니 3차원 컴퓨터그래픽에서는 픽셀마다 알파 채널이 아니라 Z buffer 값이 부가 정보로 들어가기도 한다.

3. 구 그리기

중고교 미술 시간에는 4B 연필 한 자루 들고 스케치북에다가 구를 그리는 데생(?) 실습을 해 보고.. 이과 나와서 컴공 전산을 전공한다면, 구 렌더링 정도는 C 코딩으로 저수준부터 뚝딱뚝딱 짜 봤으면 싶다.
둘이 매우 훌륭한 대조가 되리라 생각된다~! 후자의 경우, 구를 렌더링 하라고 openGL 셰이더 명령 한 줄 던져주고 끗~~이 아니라, 저 모든 픽셀의 RGB 값을 직접 계산해서 구하는 것을 말한다.

(본인이 직접 그리거나 생성한 그림이 아니니 오해하지 말 것! ㄲㄲㄲ)

이 픽셀이 구의 영역에 포함돼 있는지, 있다면 거리가 얼마나 되는지를 구의 방정식으로부터 구하고, 광원으로부터는 거리가 얼마나 되고 빛과 면이 접하는 각도가 어찌 되는지.. 최종적으로 밝기가 얼마가 돼야 하는지를 직접 공식 집어넣어서 계산으로 구한다는 뜻이다.

그림자까지 생각하면 일이 너무 어려워질지 모르니 필수가 아닌 옵션으로 남긴다만, 구 자체만이라도..;;
그럼 이 엄청난 계산을 실시간 애니메이션 수준으로 해내는 오늘날 PC와 폰의 그래픽 카드들이 얼마나 대단한 물건인지도 알 수 있을 것이다.

이런 이론 공부 잉여질 체험을 회사 취업한 뒤에 직장에서 할 수는 없을 것이고, 취업 목적 코딩 학원에서 할 수도 없을 것이다. 그러니 아직 학생일 때 학교에서 해야지...!!

4. AI

요즘 아시다시피 AI니 머신러닝이니 하는 분야가 아주 각광받고 있다. 현실에서의 문제의 목표와 input/output을 머신러닝 라이브러리가 이해하고 해결할 수 있는 형태로 변환하고, 데이터를 학습시키고 결과물을 얻는 건 확실히 학교에서 맛보기로나마 가르칠 필요가 있어 보인다.

자연어 처리라든가 영상에서 뭔가를 인식하기, ‘관련 추천 아이템 제시’ 같은 분야에서 요즘 AI들은 정말 눈부시게 똑똑해지고 기술이 발달해 있다.
개인적으로 좀 개발됐으면 하는 AI는 “문자열을 보고 폰트 종류 판별하기”, 그리고 “넓은 군중 사진을 보고는 여기에 사람이 몇 명이나 있나 추산하기”이다.

요즘은 AI를 통해 없는 정보를 유추해 내서 흑백 사진도 컬러로 얼추 복원하고, 흐릿한 영상을 선명하게 바꾸기도 한다. 그런 계산 능력이면 폰트 종류 유추는 말할 것도 없고, 이런 획이 요런 모양이었으니 다른 글자는 요런 모양이어야 하겠다는 것까지 유추를 못 할 이유가 없다. 그러면 한글이나 한자 같은 폰트를 만드는 일이 노가다가 줄어들고 한결 수월해질 것이다.

군중 사진에서 머릿수 카운트도.. 쉬울 것 같으면서도 은근히 어려울 수 있어 보인다. 하지만 기술적으로 불가능한 일은 절대 아닐 것이다. 이를 응용하면 사진에 찍힌 쌀알이나 콩알 개수를 세게 할 수도 있다.

지금 Google 검색은 영어는 정말 사람 말을 알아듣고 인간의 두뇌 활동을 어느 정도 흉내 내는 경지에 도달해 있다. 경악스럽게 그지없다. 유튜브 동영상에서 영어 자막을 자동 생성하는 걸 보면.. 어지간한 음성은 다 정확하게 알아듣는다.

여주인공이 격투를 벌이는 어느 첩보 영화의 제목을 까맣게 잊어버려서 “2017 female spy movie”라고만 쳤는데.. 우와, 저것만 토대로 Atomic Blonde라는 영화를 딱 정확하게 알아 맞히려면 도대체 저 영화의 특성을 어디까지 다 파악하고 있어야 되는 걸까..?
정말 외계인을 고문하는 기업이 아닐 수 없다.

꼭 인텔처럼 컴퓨터의 하드웨어 근간인 반도체의 본좌가 아니어도, 마소처럼 소프트웨어의 근간인 운영체제를 꽉 독점하고 있지 않아도 된다. 그 위에서 돌아가는 소프트웨어 내지 웹 서비스 중에서도 억 소리 나는 기술을 개발할 것들이 저렇게 넘쳐난다.;;

5. 암호 해독과 번역

난해한 수수께끼 암호를 풀기 위해 과거에는 언어학자가 동원되었다. 뭐, 보이니치 문서라든가 롱고롱고 문자, 로제타석처럼 인간이 만든 난해 정보를 해독할 때야 당연히 해당 지역의 고대 언어를 아는 것이 도움이 될 것이다.
하지만 현재의 군사 내지 보안 암호는 인간이 아닌 기계가 생성하다 보니 언어적인 요소가 전혀 동원되지 않으며, 오로지 수학자의 직관만이 필요하다. 2차 세계 대전 때 앨런 튜링이 독일군 에니그마 암호를 풀 때 딱히 독일어 지식이 쓰이지는 않은 것과 같은 이치이다.

기계번역도 이와 비슷한 맥락의 변화를 겪고 있다. 기계번역 시스템을 개발하는 데 입력 언어나 출력 언어의 전문가 내지 언어학자가 동원되지 않는다. 그냥 전산학자, 데이터 과학자, 머신 러닝 전문가가 동원된다.
취급하는 언어의 고유한 특성은 기계번역 시스템의 동작에 영향을 주지 않는다는 것이 한편으로는 굉장히 섬뜩한 점이다. 기계가 자연어든 암호문이든 언어 데이터를 취급하는 방식 자체가 근본적으로 바뀐 것이다.

6. 다중 상속

객체지향 패러다임에서 다중 상속이라는 걸 생각해 보자. 클래스가 기반 클래스를 하나만 두는 게 평범하고 일반적이고 권장되는 반면, 얘는 좀 특수한 상황에서 "논란과 무리수를 감수하고라도 둘 이상 갖는 것"이라는 특성이 있다.

이걸 인생에다가 투영해 보면 좀 뜬금없는 얘기지만 일부다처...;; 내지 복수 국적과 비슷한 것 같다.
C++에서 다중 상속을 지원해 봤는데.. 이건 좀 아니다 싶었는지 후대의 객체지향 언어들은 생짜 다중 상속은 금지하고, 데이터 멤버가 없는 인터페이스에 대해서만 복수 구현을 허용했다. class A extends B implements C,D,E처럼 말인데.. 이건 일부일처다첩-_-;;;처럼 들린다.

우리나라는 조선은 말할 것도 없고 일제 시대와 대한민국 초기에 이르기까지 오랫동안.. 일부다처체는 아니지만 첩이라는 게 관행적으로 있었다.
그러다가 1960년대, 박 정희 때 사회 구조를 대대적으로 뜯어고치면서 공무원들부터 첩을 두는 게 금지되었고(있으면 직장에서 징계=_=), 완전한 일부일처제가 자리잡았다.

이게 대놓고 불륜을 조장한다기보다는.. 전근대 시절엔 지금처럼 미혼 여성이 혼자 돈 벌고 사회 생활을 하는 게 도저히 가능하거나 용납되지 않았기 때문이다. 서로 필요하기 때문에 작은 마누라라는 게 존재했었다.

이런 결혼 말고 복수 국적도.. 나라마다 허용되는 정도가 케바케이고 우리나라는 징병제 병역 때문에 더 민감한 측면이 있다. 자기 원래 국적을 유지한 채로 외국의 영주권을 취득할 수는 있지만 완전히 시민권, 국적을 취득하는 건 또 별개의 문제가 된다.
우리나라의 경우, 이 대한민국 땅에 있을 때만은 한국 국적만 행사해야 한다는 각서를 쓴 뒤에 외국인의 복수 국적 취득을 허용한다.

국적 말고 이중학적, 이중인격 이런 건 명백하게 비정상일 것이다. =_=;;

Posted by 사무엘