컴퓨터 알고리즘 문제 중에는.. "N개의 원소로 구성된 목록에서 majority.. 과반/다수파라는 게 존재하는가? 존재한다면 무엇인가?"를 구하는 문제가 있다.
목록에서 과반의 원소가 다 같은 값이면 그게 바로 majority라고 정의된다. 원소들은 꼭 대소 관계가 성립할 필요가 없고 그냥 동등성 판단만 가능하면 된다. 그러니 꼭 정수가 아니어도 된다.
또한, 반반이 아니라 과반이라는 특성상, majority는 존재하지 않거나, 유일하게 존재.. 언제나 둘 중 하나이다. 공동 1위 같은 것도 고려할 필요가 없다.
이 문제는 뭐랄까.. 단순하면서도 참 므흣하다.
일단, "목록에서 가장 자주 등장하는 원소--등장 빈도수가 가장 큰 원소를 구하시오"라고 접근하지 않는 게 핵심이다.
각 원소들의 빈도수를 일일이 관리하자면 알고리즘의 시간 복잡도가 기본이 O(n^2)에서 시작할 것이고, 균형 잡는 tree 기반의 컨테이너를 사용한다 하더라도 O(n log n)이 한계이다.
그러나 이 문제를 풀기 위해서는 일을 그렇게 크게 벌일 필요가 없다.
각 원소의 빈도수가 아니라.. "이 목록은 과반의 원소가 그냥 동일한 값인가?"라고 접근하는 게 좋다.
수학인지 논리학인지 거기에는 "비둘기집의 원리"라는 게 있다. N+1개의 물건을 N개의 상자에다 다 집어넣는다면, 적어도 한 상자에는 그 물건이 2개 이상 들어가 있다. 뭔가 미적분에서 말하는 중간값 정리처럼.. 너무 당연한 말 같은데 말이다.
그것처럼 어떤 목록에 같은 원소가 "과반"이라면 그 목록은 다음 둘 중 한 특성을 반드시 갖게 된다.
- 과반의 원소가 아무리 고르게 분산되어 분포한다 하더라도, 그 원소가 연달아 두 번 이상 등장하는 구간이 반드시 하나 이상 존재한다~! 1 1 2 1 특히 원소의 전체 개수가 짝수라면 이건 뭐.. 무조건 빼박이다.
- 만약 그게 아니라면.. 그냥 맨 마지막 원소가 다수파이다.
어, 정말 저렇게 단정할 수 있나 의아할 텐데.. 이런 과감한 주장은 다수파의 정의가 절반의 '초과', '과반'이기 때문에 성립 가능하다.
절반을 포함하는 '이상'이기만 해도 위의 조건들은 당연히 성립하지 못하게 된다. "1 2 1 2" 같은 것만 생각해 봐도 알 수 있다.
이렇듯, 다수파가 존재할 때 가질 수밖에 없는 목록 전체의 특성을 생각하면.. 다수파를 굉장히 단순한 절차만으로도 정확하게 구할 수 있다.
- 최초엔 맨 첫째 원소가 다수파라고 가정하고 후보로 지정한다. 연속 등장 횟수(이하 점수)도 1을 부여한다.
- 그 다음 원소가 후보 원소와 동일하면 점수를 1 증가시킨다. 그렇지 않으면 점수를 1 감소시킨다.
- 단, 이미 현재 점수가 0이 된 상태여서 더 감소시킬 것이 없으면 후보 자체를 지금의 새 원소로 교체한다. 그리고 점수를 1로 다시 부여한다.
- 이 과정을 모든 원소들에 대해 수행한 뒤, 현재 지정되어 있는 후보를 결과값으로 되돌린다.
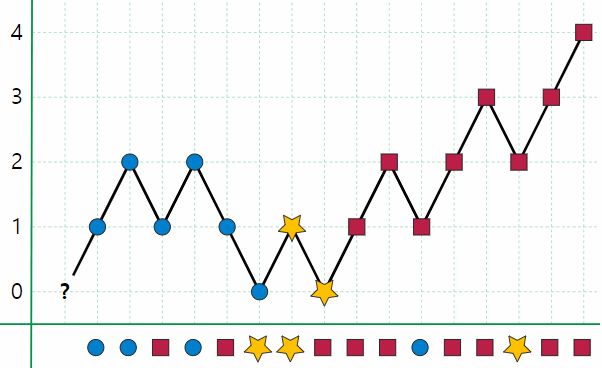
위키백과에는 이 과정을 다음과 같이 시각적으로 잘 묘사한 그림이 있더라.
정말 허무할 정도로 단순하다. 이 알고리즘은 고안자의 이름을 따서 Boyer-Moore majority vote algorithm이라고 명명되어 있다. 1981년에 학계에 처음으로 발표됐다고 하는데.. 동작하는 방식을 보니 후보, vote 이란 워딩이 적절해 보인다.
Boyer-Moore 이거 혹시 "문자열 검색 알고리즘에도 나오는 이름이 아닌가?"라는 생각이 들 텐데.. 정확하다. 동일한 명칭이다. ㄲㄲㄲㄲ
단, 위의 알고리즘은 목록에 다수파라는 게 실제로 존재하지 않더라도 언제나 후보를 갖고 있다가 되돌린다. 그러니 목록에 다수파가 존재한다면 정확한 답을 되돌리지만, 애초에 다수파가 존재하지 않는다면 뭔가 임의의 엉뚱한 후보를 되돌린다.
그렇기 때문에 이 알고리즘에는 2nd-pass, 즉 후처리라는 게 필요하다. 앞의 1st-pass를 통해 구해진 후보가 진짜로 다수파가 맞는지, 얘만 개수를 처음부터 다시 세어 보는 것이다.
1st-pass 때 쓰였던 점수 변수는 증가했다가 감소하기를 반복했기 때문에 정확한 개수가 담겨 있지 않다.
이거 무슨 분수· 무리방정식을 풀고 나서 검산을 해서 무연근을 제거하는 것과 비슷한 느낌이다.
자, 두 pass 모두 시간 복잡도는 O(n)이고, 공간 복잡도는 지역변수 꼴랑 한두 개.. O(1)에 지나지 않는다. 정말 놀랍지 않은가?
얘는 알고리즘 자체는 쉽게 이해할 수 있지만, 정말 이렇게만 해도 언제나 문제에 대한 정확한 답이 구해지는지 correctness를 이해하는 게 좀 빡셀 수 있는 문제이다.
알고리즘이라 하면 복잡한 기법을 동원해서 무식하게 풀었을 때 O(n^2)짜리인 것을 O(n log n)으로 낮춘다거나, 팩토리얼/지수함수 급인 것을 O(n^2)나 O(n^3)으로 낮추는 형태인 게 많다.
그러나 최적화를 통해서 이렇게 O(n)을 만들 수 있는 문제는 흔치 않아 보인다.
이 다수파 구하기와 성격이 아주 비슷한 문제는 N개의 숫자 목록 내부에서 "합이 가장 큰 연속된 구간을 찾기"인 것 같다. 당연히 양수와 음수가 뒤죽박죽 섞여 있는 목록에서 말이다.
정답이 (x~y) 구간은 그야말로 1<=x<=y<=N 아무렇게나 가능하기 때문에 이것도 언뜻 보기에는 시간 복잡도가 O(n^2)이나 최하 O(n log n)이 될 것 같다. 그러나 얘도 아주 간단한 검사만 하면서 시간 복잡도 O(n)과 공간 복잡도 O(1) 만으로 아주 빠르게 풀 수 있다.
- 정답 구간이 맨 첫 원소에서 시작된다고 가정하고 각 원소들을 쭉쭉 더해 본다. 그 합이 지금까지 구한 max보다 더 크면 최대값을 갱신하고 정답 구간도 업데이트 한다.
- 그런데 그러다가 합이 음수가 돼 버리면... 그러면 지금까지 살펴봤던 구간은 "더 살펴볼 필요가 없고" 그냥 통째로, 아무 미련 없이 버리면 된다. 그 다음에 양수가 나오는 구간부터 시작점을 새로 설정하고 동일한 과정을 반복한다.
더 살펴볼 필요가 없기 때문에 시간 복잡도 O(n)이 가능한 것이다. 이게 아까 다수파 문제에서 점수가 음수가 돼 버린 시점에서 후보를 깔끔하게 바꿔 버리는 것과 비슷하다. 왜 이렇게 해도 되는지를 생각하는 게 이 문제의 관건이다.
Posted by 사무엘


