디지털 컴퓨터가 취급하는 데이터라는 건 (1) machine word 하나에 다 들어가고 함수 인자에 값이 그대로 전해지는 primitive type이 아니면.. (2) 별도의 메모리를 할당해서 저장하고, 평소엔 그 메모리 주소를 가리키는 포인터만 대신 취급하는 complex type 이렇게 둘로 나뉜다.
그럼 primitive type은? (1) 정수, (2) 포인터, (3) 아니면 부동소수점으로 종류가 크게 나뉘는 것 같다.
문자열은 complex type이고, 문자 하나는 정수라는 primitive type에 속한다.
포인터는 물리적인 형태는 정수와 다를 바 없지만 그 숫자값의 성격, 의미와 용도가 여느 정수와는 전혀 다르다. 그리고 특정 프로그래밍 언어 이념이나 프로그래머의 편의를 구현하기 위해, 무슨 오프셋이나 카운터 같은 부가 정보를 곁들인 약간 뚱뚱한 포인터도 있다. (스마트 포인터, 자기 함수나 클래스의 바깥 문맥도 지원하는 포인터, 다중 상속을 지원하는 멤버 함수 포인터 등등~)
다음으로 부동소수점이 있다. 얘 역시 완전 별개의 영역이다. 얘는 잘 알다시피 과학 시간에 배우는 x.xxxx * 10^yy 이러는 숫자 표기법을 2진법 기반으로 컴퓨터에다 구현한 것이다. x를 mantissa, y를 exponent라고 한다.
얘는 딱딱 떨어지는 이산적인 정보를 좋아하는 컴퓨터에다가 현실의 연속적인(실무 또는 수학 계산) 계산값을 표현하려 애쓴 근성의 산물이다.
부동소수점은 자리수와 관계 없이 유효숫자가 일정하게 보장된다. 그렇기 때문에 -1 ~ 1 사이의 0.xxx 구간이 압도적으로 제일 정밀하다. 32비트건 64비트건, 부동소수점으로 표현 가능한 수의 무려 절반이 -1과 1 사이에 치우쳐 있다. 절대값 1 이상인 양수 지수부와, 그렇지 않은 음수 지수부가 반반씩이니까 말이다~!!
그리고 그 안에서도 0과 0.5 사이에 표현 가능한 수와 0.5와 1 사이에 표현 가능한 수는..?? 지수부의 크기에 비례해서 수백 배 이상 폭발적으로 차이가 난다. 이게 부동소수점의 심오한 세계이다. =_=;;
숫자가 커질수록 표현 가능 구간이 급격히 듬성듬성해지니.. 가장 흔히 쓰이는 축에 드는 32비트 single 부동소수점 기준으로 숫자가 1700만 정도로 커지고 나면 정밀도가 1이 되어 정수와 다를 바 없어진다.
또한, 1/2^n 형태가 아닌 모든 소수점은 원래 형태 그대로 정확하게 표현되지 못하고 유효숫자 이후의 뒷부분이 버려진다. 이 점 역시 감안해야 한다.
부동소수점 숫자를 하나 받아서 이 수의 바로 다음 크기인 수를 구하는 알고리즘을 구현해 보면 어떨까 싶다..;;
이 외에도.. x86에서는 정수끼리 나눗셈을 시키면 몫과 나머지가 같이 구해져서 레지스터에 저장된다. 그리고 0으로 나누는 건 CPU 차원에서의 오류/예외로 처리된다.
그러나 부동소수점에서의 나눗셈은 나머지라는 개념이 없다. 그리고 0으로 나눈 결과는 그냥 NaN이라는 값으로 처리된다. 이런 식으로 서로 관점과 동작이 차이가 있다.
초기화되지 않은 부동소수점 변수는 프로그래밍 언어 차원에서 NaN으로 초기화하는 게 한 가지 방법일 것 같다. NaN이 '쓰레기값' 역할을 수행하는 셈인데.. 내 기억으로 D 언어가 이걸 실제로 수행한다고 한다.
그리고 IEEE754 부동소수점 규격을 보면 NaN도 아직 에러까지는 아닌 quiet NaN, 그리고 에러인 signalling NaN으로 나뉘어 있다.
현실의 프로그래밍 언어에서는 IEEE32 (single, float) 내지 64 (double) 이 둘만을 제일 많이 볼 것이다. 당장 마소 Excel이 취급하는 숫자의 자료형만 해도 64비트 double이다.
그러나 사실은 표준 규격으로나 역사적으로는 이보다 더 다양한 부동소수점 규격이 존재한다.
| mantissa | exponent | |
| IEEE16 | 11 | 5 |
| IEEE32 | 24 | 8 |
| IEEE64 | 53 | 11 |
| IEEE128 | 113 | 15 |
| IEEE256 | 237 | 19 |
| MBF32 | 24 | 8 |
| MBF64 | 56 | 8 |
| Turbo Pascal Real | 40 | 8 |
| long double (IEEE80) | 65 | 15 |
같은 공간 안에서 유효숫자 개수와 표현 가능한 자리수 구획을 정하는 건 꽤 미묘한 고민거리인 것 같다. 한 가지 확실한 건 전체 공간이 커지더라도 exponent는 그에 비례해서 쭉쭉 커질 필요가 없으며, 로그함수 급으로 아주 느리게 증가해도 된다는 것이다. (비율이 갈수록 작아짐) 말 그대로 2의 exponent 승만큼의 자리수를 표현할 수 있기 때문이다.
exponent가 8만 돼도 0이 38개나 붙은 자리수를 표현할 수 있고, 바이트 경계가 딱 나뉘어서 처리하기 편하다. 그렇기 때문에 어지간한 부동소수점 규격들이 얘를 8비트로 잡은 걸 볼 수 있다.
MBF는 오늘날 같은 IEEE754 표준 규격이란 게 등장하기 전, 1980년대 마소의 BASIC 언어에서만 독자적으로 쓰였던 규격이다. 빌 게이츠와 폴 앨런이 젊은 시절에 나름 이런 것까지 독자적으로 만들어서 구현했다니..
MBF32는 IEEE32와 공간 크기와 분배 배율이 동일하지만, 비트 배치 순서가 다르다. 그렇기 때문에 서로 바이너리 차원에서 곧바로 호환되지는 않는다.
mantissa와 exponent 모두 내부적으로 부호 비트가 존재한다. 전자의 부호는 표현하는 숫자 자체의 양-음 여부를 결정하며, 후자의 부호는 숫자가 1보다 큰지 여부를 결정하게 된다.
저 표에서 mantissa-1을 3.3으로 나누면 (3.3의 의미는 ln(10)/ln(2)의 근사값) 10진법 기준의 유효숫자 개수가 나온다.
그리고 표현 가능한 범위도 exponent-1을 3.3으로 나누면 10진법 기준의 표현 가능 최대 자리수가 나온다.
맨 위의 16비트 부동소수점은 half-precison floating point라고 불리는데, 유효숫자가 3개밖에 안 되고 5비트짜리 exponent로는 최대 자리수도 겨우 10000대밖에 안 된다. 그러니 실용적인 가치는 매우 낮지만 이런 숫자도 머신러닝 계산용으로는 쓰이는가 보다. 그렇기 때문에 FP16이라는 옵션도 있는 거겠지?
그리고 볼랜드의 16비트 파스칼 컴파일러에만 전무후무 존재했던 6바이트 Real은 존재가 참 독보적이다. 4도 8도 아닌 그 중간.;;
부동소수점은 그 구조상 숫자 2개를 조합해서 한 숫자를 표현하니, 각종 산술 연산이나 비교 따위가 정수를 취급하는 것보다 무겁고 부담스럽다. 특히 자칫 잘못하면 동일한 숫자를 표현하는 방식이 여러 개 존재할 수 있게 되니, 이를 방지하기 위해서 자리수를 일정하게 맞추는 '정규화'라는 규칙이 필요하다.
그리고 부동소수점 연산은 초딩 시절에 배웠던 어림셈과 비슷한 면모가 있다. 아주 큰 수에다가 아주 작은 수를 많이 더하면 오차가 쌓이고 결과가 안 좋아진다.
쌍팔년도 시절엔 부동소수점 연산을 하드웨어 가속으로 보조해 주는 CPU 애드온이 별도로 존재했다. 일명 FPU, 코프로세서.. 그 시절엔 이거 하나만으로도 존재감과 가격이 지금으로 치면 고급 게임용 GPU나 마찬가지였다.
286~486 시절엔 모든 컴퓨터에 코프로세서가 있는 게 아니었다(486은 제일 저가 깡통 모델인 SX만). 그렇기 때문에 그 시절의 컴파일러들은 부동소수점의 처리 방식을 지정하는 옵션이 있었다. 무슨 x87을 지원할지, 그런 FPU 코프로세서가 없는 경우를 대비한 소프트웨어 연산 처리 코드를 넣을지를 말이다. =_=;;
자고로 컴퓨터 프로그램이라면 정수나 포인터를 어떤 형태로든 취급하지 않고 동작한다는 건 거의 불가능하다.
그러나 부동소수점을 전혀 취급하지 않는 프로그램은 분야에 따라서는 얼마든지 있을 수 있다. 그러니 부동소수점을 더 빠르게 다루는 건 소프트웨어로나 하드웨어로나 오랫동안 추가 옵션으로 간주되었던 것이다.
하드웨어 현질 없이 소수점 연산을 빠르게 하기 위해서 고정소수점이라는 편법도 쓰였다. 기존 정수에다가 자리수만 기계적으로 옮기고 곱셈과 나눗셈 결과를 보정하는 것 말이다. 32비트 정수를 16:16 내지 26:6 이런 식으로 분할했다. 단점과 한계가 명백하지만 이게 성능 하나는 워낙 탁월하니.. 옛날 게임이나 폰트 엔진 같은 일부 분야에서 제한적으로 쓰였다. ㄲㄲㄲㄲㄲ
그러다가 펜티엄이 돼서야 부동소수점 명령이 CPU에 기본 내장되고 지원되게 됐다. 그랬는데 그 펜티엄에서 바로 FDIV 나눗셈 결함이 발견되기는 했지만.. 가정용 컴에서까지 걱정해야 할 무슨 심각한 보안 문제 급은 아니었다. 아주 극단적으로 크거나 작은 수를 다룰 때 아주 미세하게 발생하는 문제이기 때문에.
80비트 long double의 경우, x87 프로세서에서도 지원 자체는 한다. 심지어 더 작은 32/64비트 부동소수점을 다룰 때도 중간 계산 결과는 다 80비트로 취급하기도 한다. 그러나 x87 이후에 도입된 SIMD 명령은 80비트 부동소수점을 지원하지 않기 때문에 80비트가 사실상 봉인돼 버렸다.
이거 무슨 분당선 전철이 훗날 8량 편성으로 고정되면서 처음에 미리 만들어졌던 수서-오리의 10량 기준 승강장의 일부 영역이 봉인된 것과 비슷한 것과 비슷한 느낌이다.;; ㅋㅋㅋㅋㅋ
하물며 128이나 256비트짜리 초대형 부동소수점은 어디 쓰이는 곳이 있기는 한지 잘 모르겠다.
본인이 과거에 만들었던 프로그램 중에 부동소수점 연산을 많이 하는 축에 드는 놈으로는 "3차원 그래픽 시연 프로그램"이 있다. 빌드된 실행 파일을 들여다보면 x87 명령이 많이 쓰인 게 눈에 띄었다.
그런데 얘를 컴파일러를 업글해서 다시 빌드하니 코드의 레이아웃이 싹 바뀌었다. x87의 구닥다리 fmul fld fadd fstp 대신, addsd movaps mulsd 처럼 SIMD 명령이 쓰인 것이다.
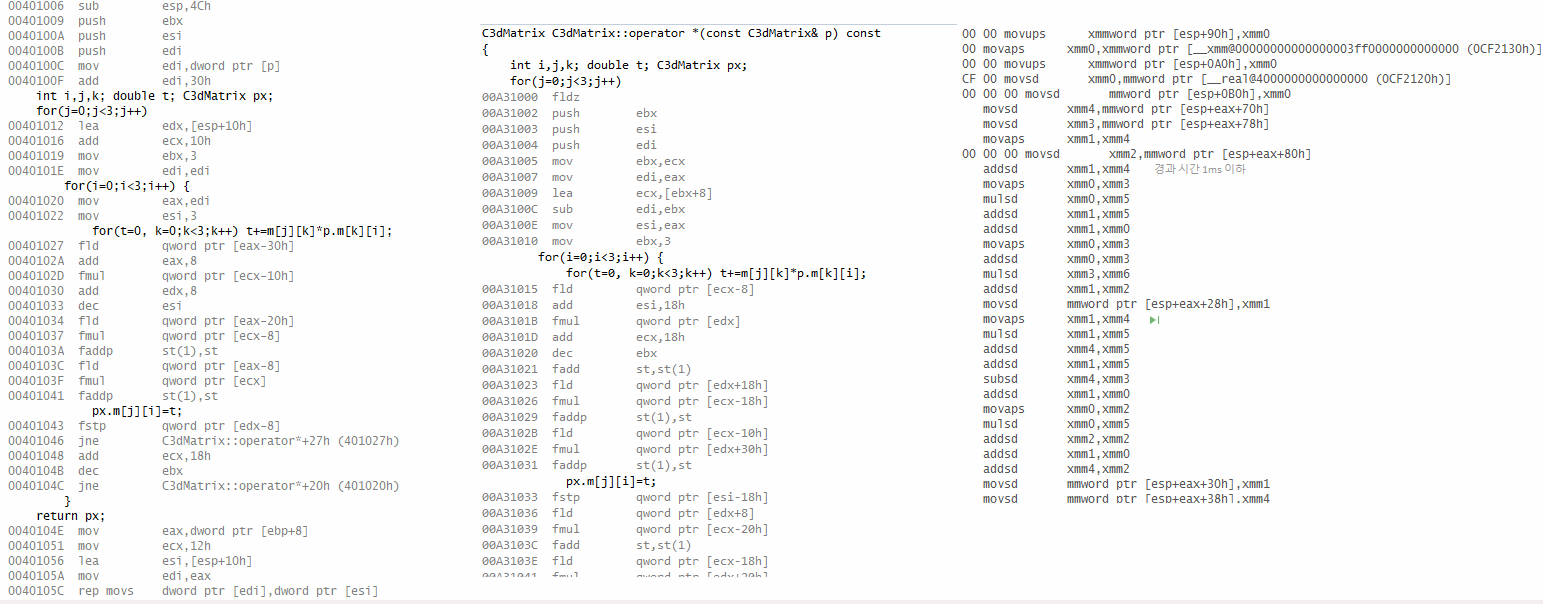
얘는 부동소수점 한둘의 연산을 넘어, 벡터· 행렬 같은 여러 데이터의 연산을 한 명령으로 한꺼번에 처리해 주는 확장 명령이다. 1999년, 펜티엄 III에서 도입됐다.
이미 Visual C++ 200x 시절부터 이 명령을 사용해서 컴파일하는 옵션이 /arch에 딸려 있긴 했다. 그러다가 2012부터는 별다른 옵션이 없으면 이 명령 세트를 사용하는 게 디폴트가 됐다~!!
이게 예전 198~90년대에 x87 명령 사용 여부와 비슷한 컴파일 옵션인 셈이다. 2012에서는 Windows XP 지원도 공식적으로는 최초로 끊겼는데 참 많은 변화가 있었다.
이상이다. 부동소수점과 관련하여 할 말한 얘기가 생각보다 많았다. ^^
x87에는 사칙연산뿐만 아니라 제곱근, 삼각함수, 2를 밑으로 하는 지수와 로그 같은 간단한 초월함수까지 CPU 명령 하나로 해치워 준다. 그러나 그렇다고 모든 수학 함수를 지원하는 건 아니어서 e를 밑으로 하는 지수와 로그는 지원하지 않는다. 2는 지원하고 e는 지원하지 않는다니.. 진짜로 수학 대신 컴퓨터 지향적인듯. ㅎㅎ
그러니 CPU빨이 없는 수학 함수는 C 라이브러리에서 어떻게 구현돼 있을까..?? 궁금해진다.
그리고 부동소수점을 10진법 문자열로 변환하거나 vice versa하는 것 말이다. 이거 은근히 어렵고 번거로울 텐데? exponent와 mantissa를 다 진법 변환하면서 두벌일을 해야 하니까..
에니악 같은 초창기 컴퓨터가 그 비효율 삽질에도 불구하고 숫자를 처음부터 10진법 단위로 묶어서 표현한 이유도 이와 무관하지 않았지 싶다.
여담: 숫자 자체를 컴퓨터가 primitive로 지원하는 숫자 unit들 여러 개를 묶어서 complex type처럼 취급하는 분야는 다음과 같다.
- 수십~수백 자리 어마어마하게 큰 정수: 공개(비대칭) 키 암호화 라이브러리에서 필요하다. 금융 거래 같은 데서..;; 얘만 기막히게 빠르게 처리해 주는 정수 연산 라이브러리도 있다.
- 유리수: 부동소수점 단독으로는 유리수 하나도 정확하게 표현이 안 되니 정수 2개 분자/분모를 따로 취급한다. Windows 계산기가 내부적으로 이렇게 동작한다고 알려져 있다.
- 복소수: 부동소수점 2개를 묶어서 실수/허수를 표현한다. 수학· 과학 일부 분야에서 쓰인다. C++에 complex라는 클래스가 있는데, 템플릿 형태여서 정수만으로 구성된 복소수도 만들 수는 있다.
- 소수점만 임의의 자리수로: 전용 수학 패키지에서 쓰인다.
- 행렬· 벡터, 사원수: 더 이상의 자세한 설명은 생략한다. 게임을 포함해 컴퓨터그래픽 분야에서 쓰인다.
Posted by 사무엘


