수치로 표현된 실험 데이터로부터 규칙를 추출하여 추세를 예측하는 것은 과학과 공학에서 아주 유용하게 쓰이는 통계 기법이다.
“input이 x1과 x3일 때 실험으로부터 얻어진 output이 각각 y1과 y3이었으니, 중간에 직접 실험을 해 보지 못한 x2에서는 결과가 아마 y2가 될 것이며(내삽), 더 나아가 범위를 벗어난 x5일 때는 결과가 y5 정도로 나올 것이다(외삽).”
n개의 실험 데이터 (x_1, y_1) 부터 (x_n, y_n)이 있다고 치자. x는 input이요, y는 output을 가리킨다. x_1...n은 꼭 균일한 등차수열 간격으로 분포해 있을 필요는 없다.
우리는 이 실험 데이터의 추세를 잘 나타내는 함수 F(x)를 얻고 싶다. F는 간단히는 그냥 직선을 나타내는 일차함수일 수도 있고 이차나 삼차, 혹은 임의의 계수를 지니는 지수나 로그 함수일 수도 있다.
그 디테일이 어떠하든 F(x_1)은 y_1과 최대한 비슷한 값이 나오고 그런 식으로 1부터 n 사이에 있는 자연수 i에 대해서 F(x_i)는 y_i와 최대한 비슷한 값이 나오면 된다. 그럼 그 F는 실험 데이터의 특성을 잘 나타내는 좋은 함수로 여겨질 것이며 내삽과 외삽에 활용될 수 있다.
최대한 비슷하다는 걸 수학적으로 어떻게 엄밀하게 표현할 수 있을까? i=1...n에 대해, 함수값과 실제 데이터의 차이인 F(x_i)-y_i가 작아야 할 것이다. 오차라는 건 양이든 음이든 절대값이 중요한데 절대값은 미분 같은 수치해석적인 처리가 어려운 연산이니 이럴 때 제곱이 쓰인다. 데이터의 분산을 구할 때와 같은 접근 방식이다. 결국 문제는
각 데이터들에 대한 오차들의 제곱의 합 = (F(x_1)-y_1)^2 + (F(x_2)-y_2)^2 + (F(x_3)-y_3)^2 … (F(x_n)-y_n)^2
이것을 최소화하는 F를 구하는 것으로 귀착된다.
그래서 이 계산법의 이름이 최소자승법/최소제곱법(least square method)인 것이다.
최소자승법이 하는 일은, 그 F(x)가 여러 함수들의 합으로 이뤄질 때, 각 함수들에 들어가는 적절한 계수를 구해 준다.
가령 F(x)가 계수가 3개 존재하는 2차함수여서 a*x^2 + b*x + c 의 형태라면, F(x) = a*f(x) + b*g(x) + c*h(x) 의 세 계수를 생각할 수 있다. 하지만 f, g, h가 실제로 무슨 함수인지는 최소자승법에서 중요하지 않다.
오차의 제곱의 합 함수를 이를 기준으로 다시 써 보면,
∑ i=1..n에 대해 ( a*f(x_i) + b*g(x_i) + c*h(x_i) - y_i )^2 가 된다.
이 식을 전개하면 제법 복잡한 항들이 줄줄이 나오겠지만, 겁먹을 필요 없다.
f, g, h는 언제든지 값을 집어넣어서 계산할 수 있는 함수이고, x_i와 y_i는 전부 상수일 뿐이다.
식에서 변수는 a, b, c이며, 제곱 버프 덕분에 오차의 제곱의 합은 a, b, c에 대한 이차식이 된다.
식의 값이 최소가 되려면, a, b, c에 대해 제각기 따로 생각했을 때, 해당 이차식의 미분계수가 0이 되는 지점에 a, b, c가 있어야 한다. 이것이 우리가 구하고자 하는 F(x)의 정체이다.
가령, x^2 + 2*x - 3 이라는 이차식을 생각해 보면, 이건 (x-1)(x+3)으로 인수분해가 되기 때문에 식의 값을 0으로 만드는 근은 1과 -3이다. 그러나 식을 x에 대해 미분하면 2*x+2가 되고 1과 -3의 중간 지점인 -1이 바로 도함수의 값을 0으로 만들어서 최소값 -4를 만들어 낸다.
우리가 풀고자 하는 문제가 다루는 식은 a, b, c 같은 여러 변수들이 존재하기 때문에, 동일한 식을 각 변수별로 편미분을 해야 한다. 그러면 다음과 같이 규칙성이 있는 3개의 연립 일차방정식이 완성된다. 세 개의 변수의 계수에 다른 변수가 포함되어서 서로 얽혀 있기도 하기 때문에, 각 변수별로 미분계수를 모두 0으로 만들 수 있는 변수들의 값은 이런 방정식을 풀어야 구할 수 있다.
2*f(x_i)*f(x_i)*a + 2*f(x_i)*g(x_i)*b + 2*f(x_i)*h(x_i)*c - 2*f(x_i)*y_i = 0 (a에 대해서)
2*g(x_i)*f(x_i)*a + 2*g(x_i)*g(x_i)*b + 2*g(x_i)*h(x_i)*c - 2*g(x_i)*y_i = 0 (b에 대해서)
2*h(x_i)*f(x_i)*a + 2*h(x_i)*g(x_i)*b + 2*h(x_i)*h(x_i)*c - 2*h(x_i)*y_i = 0 (c에 대해서)
변수가 3개보다 더 많더라도 결국은 이런 패턴의 식이 나온다! _i로 표현된 건 합계를 다 해 줘야 한다는 걸 잊지 말고.
고맙게도 양변은 2로 나눠 버리기 딱 좋게 돼 있으며, 상수항은 음수로 나와 있으니 우변으로 옮기기도 좋다.
위의 식은 결국 다음과 같은 Ax=b 꼴의 행렬로 너무나 깔끔하게 나타낼 수 있다. (행렬은 전치행렬과 자신이 서로 동일한 대칭행렬이다.)
[ F*F F*G F*H ] [ a ] [ F*y ]
[ G*F G*G G*H ] [ b ] = [ G*y ]
[ H*F H*G H*H ] [ c ] [ H*y ]
그리고 우리가 구하고자 하는 계수 벡터 x는 A의 역행렬에다가 b를 곱하면 구할 수 있다. 참 쉽죠?
이것이 행렬의 힘이다.
<날개셋> 타자연습에서 타자 속도 그래프를 얼추 비슷한 곡선 함수로 표시해 주는 기능,
그리고 엑셀에서 추세선을 그어 주는 기능들도 다 이 최소자승법 알고리즘을 써서 구현되어 있다.
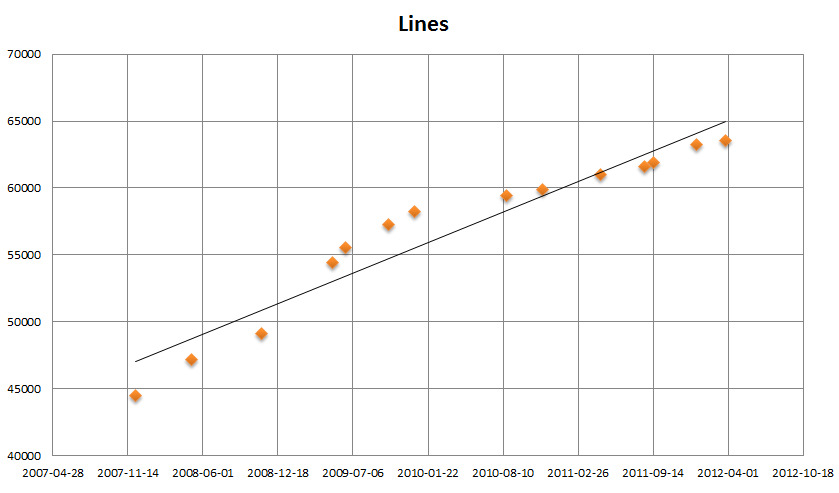
아래의 그림은 지난 5년간 <날개셋> 한글 입력기의 전체 소스 코드 라인 수의 증가 추이와, 이를 토대로 최소자승법으로 구한 추세선(직선) 그래프이다. 2009년 상반기에 5.3 버전이 개발되었을 때 약간 가파르게 소스 코드가 증가했지만, 그 후로는 증가가 비교적 원만했음을 알 수 있다. 1년에 약 4천 줄 꼴로 코드가 증가한 것인지?
Posted by 사무엘


