1. 평행사변형의 넓이, 평행육면체의 부피
2*2 크기의
(a b)
(c d)
행렬이 있을 때, 이 행렬의 행렬식이라고 불리는 D 값은 a*d - b*c로 정의된다. ax+by = 얼마, cx+dy = 얼마 요런 방정식의 근을 구하는 식을 세워 보면 행렬식은 x, y의 분모에 들어가 있다. 그러니 이 값이 0이면 근은 부정이나 불능으로 빠지게 된다.
한편, 행렬식에는 기하학적인 의미가 있다. 원점에서 (a,b)를 잇는 선분이 가로변, 원점에서 (c,d)를 잇는 선분이 세로변인 평행사변형의 넓이를 나타내기 때문이다.
그도 그럴 것이 이 행렬은 한 변의 길이가 1인 (0,0), (1,0), (1,1), (0,1)이라는 정사각형을 (a,b), (a+c, b+d), (c,d)라는 평행사변형으로 옮긴다. (a+b)*(c+d)라는 전체 직사각형에다가 주변의 합동인 삼각형 두 쌍의 넓이를 빼면, 평행사변형의 넓이로 남는 것은 ad-bc뿐이다. 아래 그림을 보시라.
(a+c)(b+d) - b(a+c) - c(b+d) = d(a+c) - c(b+d) = ad + cd - bc - cd = ad-bc
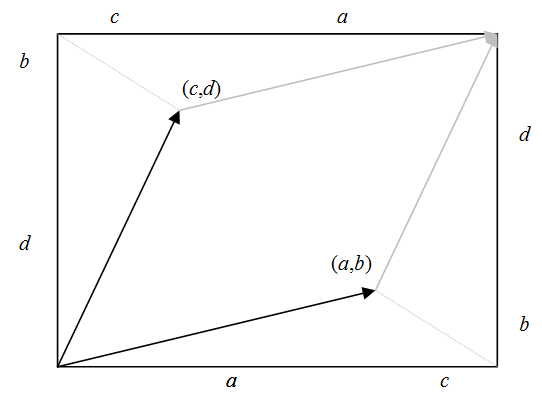
이 평행사변형에서 대각선을 구성하는 (a,b)와 (c,d)를 연결하면 사각형을 반으로 쪼갤 수 있다. 다시 말해 원점과 (a,b), (c,d)를 꼭지점으로 하는 삼각형의 넓이는 ad-bc의 절반이 된다.
다음으로..
저렇게 두 점 A(ax, ay)와 B(bx, by)가 있을 때, A-원점-B 자취의 방향을 판단하는 공식이 있다(시계 방향인지 반시계 방향인지). bx*ay - by*ax이며, 여기에는 배후에 삼각함수 sin( alpha-beta )가 숨어 있다.
그런데 위의 두 점 (a,b), (c,d)도 코싸인/싸인 alpha와 코싸인/싸인 beta라는 극좌표 형태로 표현하면, 행렬식 a*d-b*c 역시 결국은 sin( alpha-beta )과 패턴이 동일함을 발견할 수 있다. 두 쌍의 숫자를 각각 서로 엇갈리게 곱해서 빼는 것 말이다.
이렇듯, 행렬식에 두 벡터의 사잇각에 대한 삼각함수 값이 들어있으니, 벡터의 길이만 정규화하면 각도를 구할 수 있다. 또한 두 변의 길이와 그 사이의 끼인각을 알고 있는 삼각형의 넓이는 A*B*sin(theta)/2로 간단하게 결정된다.
그리고 이 식을 확장하면 삼각형뿐만이 아니라 여러 삼각형들로 분해 가능한 단순다각형(선분들이 서로 만나지만 않으며 볼록하거나 오목할 수 있음) 넓이 내지 폴리곤 패스 방향을 구할 수도 있다. 넓이와 방향(넓이의 부호)이 같이 구해진다.
2차원에서는 이 정도로 분석이 되고, 3차원으로 가면 어떨까?
짐작했겠지만 3*3 행렬의 행렬식은 그 행렬을 구성하는 3개의 벡터들을 축 내지 기저로 삼는 평행육면체의 부피와 같다. 직교좌표에서 모든 점들의 최대치에 해당하는 직육면체의 부피에다가 또 모서리 주변의 온갖 사면체들의 부피를 빼야 하니 식이 굉장히 복잡할 것이다. 3*3 행렬의 행렬식이 항이 6개나 되고 2*2의 것보다 훨씬 더 복잡한 것은 이 때문이다.
하지만 3차원에서도 언제나 부피만 구하는 건 아니다.
차원만 2차원이 아닌 3차원으로 확장한 뒤, 원점에서 출발하는 두 벡터를 가로변 세로변 축으로 삼는 평행사변형의 넓이는 어떻게 구하면 좋을까? (삼각형의 넓이도 당연히 자동으로 포함) 즉, 3차원 공간 안에서의 2차원 평면인 것이다. 이건 2*2 행렬식보다는 어렵겠지만 3*3 행렬식보다는 쉬울 것이다.
그리고 이것이 바로 벡터의 '외적'(벡터곱) 연산이 하는 일이다. 아마 고등학교에서는 내적까지만 하지 외적은 안 배우지 싶다. 단, 내적부터 먼저 개념을 좀 복습해 보자.
2. 벡터의 내적
왜 각 성분을 차례대로 곱한 것을 더하면 내적이 나오는 걸까?
이 원리의 배후에는 코싸인 제2법칙이 있다.
아까 두 변의 길이(두 선분의 길이를 각각 A와 B라 하자)와 그 사이의 끼인각을 아는 삼각형의 넓이를 구했는데, 이 경우 삼각형이 유일하게 결정되었으므로 나머지 한 변의 '길이' C도 당연히 구할 수 있다. 그 삼각형의 모든 특성이 파악 가능한 것이다. C^2 = A^2 + B^2 - 2*A*B*cos(theta) 이다.
이건 피타고라스의 정리의 일반적인 경우이며, 증명하는 방법이 상당히 많다. 여기에서는 제일 직관적인 해석학적 방법 하나만 소개하고 넘어가겠다.
선분 A와 B가 원점을 지나고 선분 A는 x 축에 평행하다고 한다면 선분 A는 (0,0)과 (a,0)을 지나게 될 것이며, 0도인 선분 A로부터 theta도만치 떨어진 선분 B는 선분 B는 (0,0)과 (b*cos(theta), b*sin(theta))를 지난다. 임의의 차원의 임의의 위치에 있는 어떤 삼각형 ABC라도 변환을 통해 그렇게 2차원 평면에서의 일반화가 가능하기 때문이다.
그럼 선분 C의 길이는 저 (a,0)과 (b*cos(theta), b*sin(theta)) 사이의 거리와 같다. 그러므로 길이의 제곱은 (a - b*cos(theta)^2 + (b*sin(theta))^2 가 된다.
이 식을 풀면 a^2 - 2*a*b*cos(theta) + b^2*cos(theta)^2 + b^2*sin(theta)^2 가 된다.
b^2항은 cos(theta)^2 + sin(theta)^2 이므로 1로 약분돼 없어지고, 결국 코싸인 제2제곱 공식이 고스란히 나온다.
그럼, A, B, C를 이제 벡터라고 생각하고 2차원이 아니라 각 축별 좌표를 코싸인 제2제곱 공식에다 대입해 보자.
A=(a1,...,an), B=(b1,...,bn) 같은 식이다. C는 두 벡터의 차이 A-B와 같다.
벡터의 절대값의 제곱은 잘 알다시피 거리의 제곱과 같기 때문에 각 성분들의 제곱을 모두 더한 것과 같다. 그러므로
∑ [i=1..n] (ai^2 + bi^2 - 2*ai*bi) = ( ∑ [i=1..n] (ai^2 + bi^2) ) - 2*A*B*cos(theta) 로 식이 대충 떨어진다.
A와 B에서 각 성분들의 제곱을 합을 구하는 부분은 좌우변 공통이므로 소거되고.. 남는 것은
2*A*B*cos(theta) = ∑ [i=1..n] 2*ai*bi 이다. 여기서 양변을 2로 나눠 주면 내적 공식이 아주 깔끔하게 유도된다. 콜?
벡터의 내적은 그냥 숫자 하나(스칼라)만으로 답이 떨어지며, 벡터의 각 성분들을 차례대로 곱해서 더하기만 하면 된다. 내적에는 두 벡터의 사이각의 '코싸인' 값이 들어있기 때문에, 두 벡터가 서로 수직인지를 벡터의 길이와 무관하게(= 정규화 안 하고도) 간편하게 판별할 수 있다. 코싸인 90도는 0이므로!
내적은 계산이 딱히 어렵지 않을 뿐만 아니라, 2차원이고 3차원이고 어느 차원이든지간에 계산법이 동일하다는 것도 큰 장점이다. 두 벡터의 사이각을 구하는 용도로는 완전 딱이다. cos(alpha-beta) = cos(alpha) cos(beta) + sin(alpha) sin(beta) 인 것에도 2차원일 때의 내적 공식이 숨어 있다는 걸 발견할 수 있다.
또한, 생긴 모양 덕분에 벡터의 내적을 행벡터(행이 하나. 수평선-_-)와 열벡터(열이 하나. 수직선)의 곱으로 표기하기도 한다. (행과 열뿐만이 아니라 횡과 종도 어느 게 어느 건지 종종 헷갈릴 때가 있다만..;;)
3. 벡터의 외적
그에 반해 외적은 결과값도 벡터이다. 그리고 3차원일 때에만 정의된다. 계산값의 각 차원과 피연산자들이 일대일로 딱 밀착해 있는 관계로 3차원 말고는 선택의 여지가 없기 때문이다.
성분이 (a1,a2,a3)인 벡터 A와, 성분이 (b1,b2,b3)인 벡터 B의 외적은
(a2*b3-a3*b2, a3*b1-a1*b3, a1*b2-a2*b1)이라고 정의된다.
어 그런데 이거, 두 쌍의 숫자를 각각 서로 엇갈리게 곱해서 빼는 게 2*2 행렬식을 구하는 것과 비슷해 보인다. 맞다.
그래서 벡터 A, B가 동일 평면상에 있어서 a3와 b3 같은 게 동시에 0이기라도 하면, 해당 변수가 포함된 항은 모두 소거된다. 이 경우 외적은 그냥 2*2 행렬식과 동일해진다.
또 생각할 점은.. 3*3 행렬식을 구하는 것도 특정 row와 col을 제외한 2*2 행렬식을 구하는 것의 연속이라는 점이다. 그래서 외적 구하는 공식을
(i j k )
(a1 a2 a3)
(b1 b2 b3)
의 행렬식이라고 표현하기도 한다. 물론 여기서 i~k는 스칼라값이 아니라 각각 (1,0,0), (0,1,0), (0,0,1)에 해당하는 단위벡터이다. 그러니 스칼라와 벡터가 뒤섞여 있는 저 행렬은 대수적인 의미는 딱히 없다. 외적 구하는 공식을 좀 더 뽀대나게 표현하는 용도로만 쓰이는 셔틀일 뿐이다. 그래도 결국은 3*3 행렬식과 닮긴 닮았다.
행렬식을 구하는 공식에서 j에 해당하는 부분은 더하는 게 아니라 뺀다. 그렇기 때문에 외적 공식에서는 1,3이 아니라 3,1 순서로 쓴 뒤에 더하는 것으로.. 다시 말해 양수를 빼는 게 아니라 음수를 더한다고 표현을 달리 했다. 둘 다 동일한 의미이므로 부호에 주의하기 바란다.
벡터는 스칼라와는 달리 '크기'뿐만 아니라 '방향'이라는 정보가 추가로 들어있다.
외적 연산을 통해 구해진 벡터는 일단 크기는 두 벡터의 크기의 곱에다가 사잇각의 sin값을 곱한 것과 같다. 그러므로 3차원 공간에서 두 3차원 벡터가 만드는 평행사변형/삼각형의 넓이를 구할 수 있다.
외적 식을 전개해서 크기의 제곱을 해 보면, 각각의 두 벡터의 크기의 제곱을 곱하고 거기에다 벡터의 내적값(양 벡터의 각 성분들을 서로 곱해서 더함)의 제곱을 뺀 것과 같다고 식이 전개된다. A^2 - B^2 꼴이 되기 때문에 (A+B)(A-B)로 인수분해를 하고 싶은 충동이 느껴지지만 여기서는 식을 다른 형태로 바꿔야 된다.
내적에는 역시 두 벡터의 크기의 곱에다가 사잇각의 cos이 들어 있으니 이것의 제곱이라면 두 항이 결국 |A|^2 * |B|^2를 공통으로 갖고 있고 (1 - cos^2 )가 남는다. 그리고 이것이 sin^2과 같다는 건 두 말하면 잔소리이고.
외적의 크기에 벌써 이렇게 유용한 정보가 들어있는데, 방향은 더욱 흥미롭다.
짐작하겠지만 두 벡터의 외적의 방향은 두 벡터와 수직이다. 물론 위쪽도 수직이고 아래쪽도 수직인데, 해당 좌표계의 동일 부호가 향하는 쪽으로 방향이 결정된다. 두 기저 벡터에 대한 외적을 구하면 나머지 기저 벡터가 튀어나온다.
애초에 두 벡터의 외적은 그 두 벡터와의 내적이 모두 0인 벡터 중에 크기가 저렇게 AB sin(theta)로 나오는 놈을 구한 것이다. a1*c1 + a2*c2 + a3*c3 = 0과 b1*c1 + b2*c2 + b3*c3 = 0을 만족하는 (c1,c2,c3)을 직접 구해 보면 안다. 저것만으로는 식보다 미지수 개수가 더 많으니 (c1,c2,c3)가 하나로 딱 떨어지지 않고 c1과 c2가 c3의 배수인 것처럼 관계식만 나온다. 그런데 c3의 특정값일 때 c1,c2에 있던 분모가 싹 소거되고 c1~c3이 저렇게 아주 대칭적이고 깔끔하게 나오는데 그게 바로 외적값이다.
이런 유용함 때문에 외적이 3차원에서의 전유물이라고 여겨지는 것이다. 이항연산에 딱 최적화돼 있지 않은가.
물론, 외적은 수직이라는 게 위아래가 모두 존재한다는 특성상 교환 법칙이 성립하지 않고 A×B=-B×A이다. 뭐, 4차원 이상에서는 두 벡터와의 내적이 모두 0인 벡터는 3차원일 때처럼 일직선상의 형태로 유일하게 떨어지지가 않는다. 그러니 외적과 같은 접근 방식이 큰 의미가 없어져 버린다.
끝으로, 3차원에서 벡터의 내적과 외적은 삼중곱이라는 연산을 통해 한데 만난다. 3개의 벡터 A,B,C를 축으로 하는 평행육면체의 부피를 구하고 싶으면 아까처럼 벡터들을 3차원 행렬의 행렬식으로 표현해도 되지만, 밑면에 속하는 두 벡터 A×B의 외적을 구한 뒤 거기에다 C와 내적을 구하면 된다. (A×B)·C! 그게 결과적으로 행렬식을 구한 것과 같은 계산 결과가 도출된다. 왜 그런지는 아까 그 외적 구하는 행렬과 일반 행렬의 행렬식을 늘어놓고, 거기에다가 내적을 구하는 공식까지 적용한 뒤 서로 비교하며 생각해 보면 된다.
Posted by 사무엘


