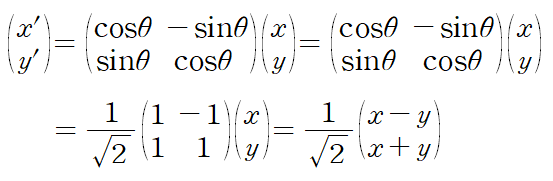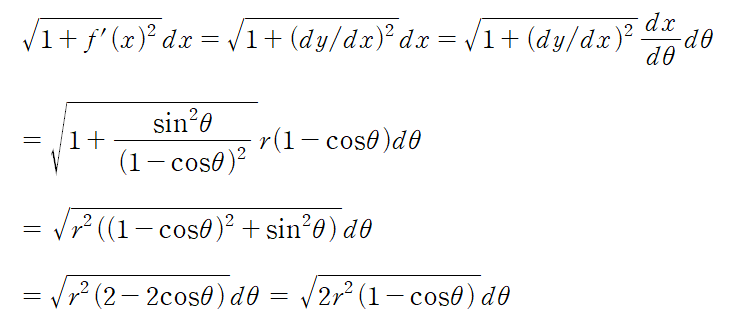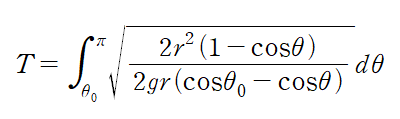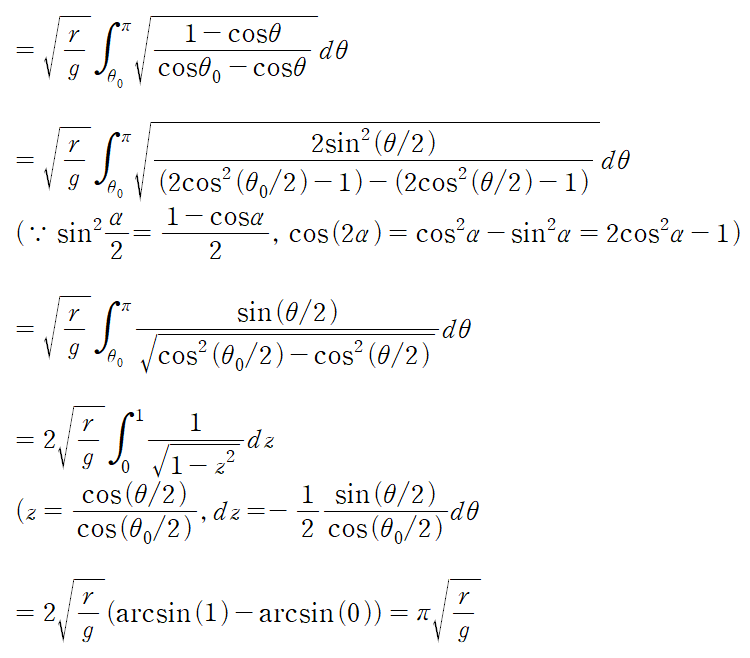김 용묵의 절대공간 - 블로그

1. 행렬의 기본연산

우리는 학교에서 방정식을 푸는 방법에 대해 배울 때, 등식에 대해 너무 당연해 보이는 원리를 배운다.
등식의 양변에 같은 수를 더하거나 빼거나 곱하거나, 나누더라도(비영) 등식은 성립한다는 거.

이건 사실 너무 당연한 얘기이다. 이미 값이 같은 두 수에다가 동일한 수로 동일한 연산을 하면 그 결과도 서로 일치할 수밖에 없다. 그런데 그 당연한 이치만 이용해서 복잡한 방정식을 푸는 게 수학의 묘미이다.
등식의 좌변과 우변을 마법 같이 변형하고 복잡한 항을 옮기거나 없애고, 궁극적으로 좌변에 x 하나만 남기니까 말이다.

그런데 행렬을 다루는 선형대수학으로 가면 이와 비슷한 방법론이 또 등장한다. 이른바 행렬을 줄 단위로 변형하는 기본 연산 말이다.
저 줄이라는 게 가로줄(row 행)인지 세로줄(col 열)인지는 중요하지 않다. 행렬에서 임의의 두 줄을 뽑아서 한 줄의 숫자를 그대로 또는 스칼라(상수)배 한 뒤, 다른 줄에다가 그대로 더해 준다. 두 벡터 A, B에 대해서 A = A + n*B 같은 셈이다.

행렬이라는 건 그냥 방정식이 아니라 변수도 여러 개, 식도 여러 개인 연립방정식을 풀기 위해 도입된 물건이다.
연립방정식을 풀기 위해서 우리가 하는 일은 식에서 변수를 하나씩 소거하는 것이다.
어떤 식은 x y z 변수가 모두 등장하지만 다음 식은 x를 소거하여 y z만 남기고, 마지막 식은 z만 남기고..
그러면 그 z를 y-z 식에다가 대입해서 y를 구하고, 이걸 x-y-z 식에다가 대입해서 x까지 모두 구하면 된다.

이 과정이 행렬로 치면 '삼각화'이다. 행렬이 나타내는 방정식의 특성(= 근)을 변형하지 않으면서 0이 아닌 숫자를 행렬의 반쪽에다가만 남기는 것이다.
그리고 그렇게 삼각화하는 수단이 바로 저 줄 단위 기본연산이다. 없애고 싶은 칸의 숫자를 스칼라배를 통해 동기화시키고 나서 빼 주면 그 칸은 0이 되어 소거된다.

행렬의 기본연산의 묘미는 바로..
한 줄 내용의 상수 배를 딴 줄에다가 아무리 더해 주더라도 행렬 내지 방정식의 전체 특성이 전혀 바뀌지 않는다는 것이다. 특히 그 행렬의 행렬식의 값이 변하지 않는다. 오로지 자기 자신을 상수 배 했을 때만 행렬식 값에도 그 배율이 반영된다.

왜? xyz축을 각각 가리키는 단위 벡터들을 생각해 보자. z축을 1만치 향하는 벡터에다가 완전히 다른 방향인 x, y축을 가리키는 벡터를 제아무리 더해 줘도 z축 방향은 영향을 받지 않는다.
커버하는 벡터 공간이 정육면체이던 것이 찌그러진 평행육면체가 될지언정, 그 육면체의 부피가 바뀌지는 않는다는 걸 생각하면 이해에 도움이 될 것이다. 오로지 z축 자체의 크기를 키워야만 육면체의 부피가 바뀔 것이다.

이 기본연산으로부터 유도 가능한 재미있는 특성이 또 있다.
행렬에서 서로 다른 임의의 두 줄을 맞바꾸는, 다시 말해 교환하는 것을 저 기본연산들의 조합으로 구현할 수 있다. 그리고 이렇게 교환을 하면 행렬식 값이 부호가 바뀐다.

• 임의의 두 줄 (A,B)가 있는데 먼저 A줄에다가 B줄 내용을 빼서 (A-B,B)를 만든다.
• 그 뒤 B에다가 지금 A줄의 값이 돼 있는 A-B를 더해 주면 B가 소거되어 (A-B,A)가 되고..
• A-B가 돼 있는 A줄에다가 지금 B줄의 값인 A를 빼면 (-B,A)가 된다.
• 이제 -B에다가 -1을 곱하면 (A,B)가 (B,A)로 교환이 완료되고.. 이때 행렬식의 부호도 -1이 곱해지면서 바뀐다. 이런 원리 때문이다. =_=;;

이 바닥에서는 피연산자의 순서가 바뀌면 결과의 부호가 달라지는 연산을 심심찮게 보는 것 같다. 벡터곱(외적)이라든가, 사원수 i,j,k끼리의 곱 같은 거 말이다. 행렬의 줄 교환 기본연산도 그런 축에 드는 셈이다.

2. 두 변수 교환

그리고 위의 저 로직은 컴퓨터 코딩깨나 하는 분들에게는 꽤 낯익을 것이다.
임시 변수를 사용하지 않고 두 변수 값을 맞바꾸는 swap 알고리즘과 개념적으로 일맥상통하기 때문이다. 즉, C 코드로 치면 아래 식을 적용한 거나 마찬가지이다. ㄲㄲㄲㄲㄲㄲㄲ

a -= b, b += a, a -= b; a=-a;

물론, 코딩을 할 때는 꼭 합성 대입 연산자에만 집착할 필요는 없으니, 피연산자의 배치 순서를 바꿔서 부호 전환을 축약시키곤 한다.

a += b, b = a-b, a = a-b;

덧셈과 뺄셈 대신, 곱셈과 나눗셈을 써도 되기는 한다. 그러나 이건 실용성이 최악이다.
그렇잖아도 임시 변수 안 쓰는 swap 자체가 실무에서는 딱히 쓰이지는 않고 "이런 테크닉도 있다" 수준으로 짚고 넘어가는 잉여이다. 근데 하물며 swap을 위해서 덧셈-뺄셈보다도 더 무거운 곱셈과 나눗셈이라고??
오버플로 가능성, 피연산자에 0이 있을 때의 문제, 부동소수점인 경우에는 오차 문제.. 정말 할 짓이 못 된다.

사실, 컴퓨터의 입장에서 이런 맞교환 용도로 덧셈· 뺄셈보다도 더 낫고 최고 적합한 연산자는 바로 비트 xor이다. 얘는 같은 피연산자를 두 번 적용하면 도로 원래 숫자로 돌아온다는 마법 같은 특성이 있기 때문이다. (A ^ B)^B = A 다시 말해 xor은 항등원이 0이고 역원은 걍 자기 자신.. 그래서 프로그래머라면 잘 아시다시피

a ^= b, b ^= a, a ^= b;

정말 매끄럽고 단순한 합성 대입 연산자 3방으로 swap이 바로 구현된다. 컴퓨터의 입장에서 xor은 산술 연산보다 속도도 더 빠르며, overflow 문제도 전무하니.. 가히 최적이다.

다만, 다시 얘기하지만 임시 변수 안 쓰는 swap은 실용성이 별로 없다.
연산이 병렬화 이념과 맞지 않으며, 실수로 a와 b에다 같거나 겹치는 메모리 주소를 줘서는 절대로 안 된다.
"하이고, swap 때 변수 하나 줄여 갖고 메모리 얼마나 절약했고 얼마나 팔짜 폈나? ㅋㅋㅋ" 이런 비아냥이 나올 만도 하다.

임시 변수 안 쓰는 swap의 자매품으로는..
O(1)을 초과하는 추가 메모리를 쓰지 않는 n log n 정렬 알고리즘(heap 정렬)이라든가 parent node가 없는 트리 자료구조를 생각할 수 있을 것 같다.
하지만 현실에서는 안정성 있는(stable) n log n인 merge sort라든가, 아예 n^2이지만 아주 가벼운 insert sort가 소규모 한정으로 선호된다. heap sort가 막 메리트가 있다고 여겨지지는 않고 있다.

그리고 parent node 없이 스스로 균형잡는 tree 자료구조의 삽입· 삭제를 구현하는 것 자체는 당연히 가능하다.
그러나 C++에서 제공하는 set, map 부류의 컨테이너들은 가벼운 포인터 기반의 iterator로 원소 순회 기능을 제공하다 보니.. 어차피 다들 node에다가 parent 포인터를 갖추고 있다.

이게 없으면 iterator가 자체적으로 스택을 가진(= 현 순회 상태를 저장) 복잡한 클래스가 돼야만 트리 내부를 순회할 수 있기 때문이다.
뭐, 노드 하나당 8바이트짜리 포인터 오버헤드가 추가됐다고 해서 요즘 세상에 컴퓨터가 메모리가 부족하다고 징징대지는 않는다. ^^

3. 여담

(1) 행렬 얘기를 하다가 프로그래밍 얘기가 너무 길어졌군..;;
아무튼 선형대수학에서 행렬을 다루는 기법을 보면 원소들을 쭉쭉 옮겨서 행렬을 ＼ 모양의 삼각형 형태로 가공하는 게 많다. 삼각형 모양이 된 행렬은 그 대각선상에 있는 원소만 쭈룩 곱하면 행렬식을 구할 수 있고 여러 모로 취급이 편하기 때문이다.

행렬식이나 역행렬을 구할 때는 행렬에다가 앞서 언급했던 기본연산을 적용하면서 행렬을 삼각화하게 된다. 그런데 이 과정을 기록으로 남겨서 원본 행렬을 아예 하삼각행렬과 상삼각행렬의 곱으로 일종의 분해를 할 수 있다. 단, 앞서 등장하는 하삼각행렬은 주대각 성분이 모두 1... 이걸 LU 분해라고 부른다.

(2) LU 분해 말고 PD(P^-1)이라는 세 형태로 행렬을 분해하는 더 어려운 기법도 나중에 다뤄진다. 이건 행렬의 고유값/고유벡터와 관계 있는 더 어려운 개념이어서 나중에 다뤄지는데.. 행렬식이 아니라 행렬의 거듭제곱을 단순한 형태로 표현하게 해 주는 아주 강력한 도구이다.

(a+b) 기호의 다항식을 n승 하면 항이 더덕더덕 늘어나는데, 이는 행렬도 마찬가지이다. 그런데 주대각성분에만 값이 붙어 있는 대각행렬은 n승 해도 항이 늘어나지 않고 마치 스칼라값처럼 자기 자신의 지수만 늘어난다.
PD(P^-1)은 행렬을 대각행렬 D를 포함한 형태로 분해하는 기법이다. 이에 대해서는 나중에 추가로 글로 정리하도록 하겠다.

(3) 임의의 a,b,c...꼴의 원소에 대해서 행렬의 곱셈뿐만 아니라 행렬식이나 역행렬을 구하는 일반적인 공식도 유도할 수는 있다. 그러나 행렬식 하나만 생각해 보면, n 크기 정사각행렬의 행렬식은 계수가 n인 항이 2n이나 n^2, 심지어 2^n개도 아니고 n!개씩 달라붙는다.;; 아시다시피 그 행렬식은 이전 n-1크기 행렬식들을 n개만치 더하고 쪼개는 걸 반복하는 형태로 재귀적으로 정의되기 때문이다.

그렇기 때문에 큰 행렬을 다룰 때 실무에서는 일반적인 공식은 사실상 의미를 갖지 않는다. 그냥 행렬에다 기본연산을 열나 적용한 뒤에 주대각 성분을 곱하고 말지. 이러면 O(n^3) 정도의 복잡도가 나온다. 얘들은 중간 계산 결과들이 저 복잡한 항의 개수를 줄여 주는 거나 마찬가지이다.

FM대로 재귀적으로 행렬식을 구하더라도 다이나믹 기법으로 이전 계산 결과를 적절히 저장하면 시간 복잡도를 팩토리얼에서 다항함수로 바꿀 수는 있을 것이다.
하지만 이건 쪼개진 sub행렬을 기술하는 게 생각보다 빡세고 쉽지 않다.;;; (직접 생각해 보면 이게 무슨 말인지 알 거임. ㄲㄲㄲㄲㄲ) 크기가 다양한 행렬들의 곱셈 횟수를 최소화하는 문제와는 상황이 좀 다르다. 그러니 이러나 저러나 FM은 실용성이 떨어진다는 건 어쩔 수 없어 보인다.

Posted by 사무엘

'초등함수'에 속하는 '초월함수'들 중에 지수함수인 e^x는 미분을 하던 적분을 하던.. 도함수나 부정적분이 전부 자기 자신과 동일한 굉장히 특이한 기본 함수이다.
지수는 저렇고, 삼각함수/쌍곡선함수는 그냥 답정너 정의에 가깝게 미분-적분 순환고리를 그냥 외운다.
그럼 e^x의 역함수인 ln x는 부정적분이 과연 어찌 될까?

ln x는 도함수가 1/x라는 간단한 형태로 정의되는 덕분에, '부분적분'으로 부정적분을 구하는 아주 교과서적인 예로 다뤄진다.
부분적분은 곱의 미분법으로부터 유도되어 두 함수 F, G의 곱에 대해

F(x)G(x) = ∫ F'(x)G(x) dx + ∫ F(x)G'(x) dx

가 된다는 원리이다. 보통은 저것보다는 순서를 바꿔서

∫ F'(x)G(x) dx = F(x)G(x) - ∫ F(x)G'(x) dx

요런 형태로 더 소개되는 편이다.
ln x의 경우, 위의 부분적분에서 F는 그냥 x로, G는 ln x를 집어넣으면 바로 풀린다. 그러면 F'(x)는 1이라는 상수가 되고 G'(x)는 1/x가 되므로

∫ ln x dx = x*ln x - ∫ x/x dx = x*ln x - x = x(ln x - 1)

이렇게 답이 구해진다. x*(ln x)' 가 x/x로 바뀌어서 1로 상쇄되는 것이 백미이다.;;

그럼 ln x의 0..1 정적분의 값은 얼마일까? 다시 말해 위의 그래프에서 선이 y축의 0 아래로 뚝 떨어지는 구간의 면적은 얼마일까?
저 역도함수에다가 0과 1을 대입해서 차를 구하면 -1임을 알 수 있다. 그러나 더 직관적으로 아는 방법도 있다.
저 구간은 ln x의 역함수인 exp(x)에서 x의 음수 구간 면적과 동일하기 때문이다.

그러니 exp(x)를 0부터 -∞까지 적분해 봐도 동일한 값을 더 쉽게 구할 수 있다. exp는 그냥 자기 함수에다 값을 대입하는 것만으로 적분값을 구할 수 있으니 말이다.

그리고 더 흥미로운 사실이 있다.
ln x의 부정적분인 x(ln x - 1)의 의미는 바로..
저 X축의 x, 그리고 Y축의 ln x라는 직사각형에서.. 맞은편의 역함수 exp(ln x) 구간의 면적을 뺀 나머지 면적이라는 것이다. -x의 의미는 바로 -exp(ln x)라는 것..!!

부분적분에서 곱을 구성하는 두 함수 중의 하나가 그냥 x 자체인 덕분에, 기하학적으로 이런 의미까지 지니게 된 셈이다.
앞서 부분적분 식에서는 x가 x*(1/x)를 적분해서 얻어졌었는데.. 여기서는 exp와 ln이 상쇄되어 얻어졌다는 게 흥미롭다.

이런 부분적분은 삼각함수 등 다른 초월함수들의 '역함수'의 부정적분을 구할 때도 요긴하게 쓰인다.
부분적분의 특성상 원함수의 도함수도 알아야 하는데, 그건 역함수의 미분법을 동원해서 구하면 된다.

다음으로, ln x를 넘어서 (ln x)^2의 정적분을 구하려면?
부분적분 패턴에서 F'(x)와 G(x)를 모두 ln x로 잡으면 된다. 그러면 F(x)는 x*(ln x -1)에 대응하고, 최종적으로는 아래와 같은 복잡한 식이 도출된다.

이를 일반화해서 (ln x)^n의 부정적분은

x*(ln x)^n - a*x*(ln x)^(n-1) + b*x*(ln x)^(n-2) ... +- z*x*(ln x) +- z*x + C (적분상수)

이런 꼴이 된다. 모든 항에 x는 기본으로 붙어 있고 그 다음에 (ln x)의 n승에 대한 항이 형성되어 항의 수는 총 n+1개..
부호는 -와 +가 번갈아가며 바뀐다.
맨 앞의 제일 고차항인 (ln x)^n의 계수는 언제나 1이지만, 그 다음 항인 a...z로 갈수록 n과 n-1, n-2... 가 차례로 곱해져서 n=2일 때는 2 2.. n=3일 때는 3 6 6, n=4일 때는 4 12 24 24... 이렇게 계수가 정해진다.

그러므로 0에서 1까지의 정적분 값은 n의 홀짝 여부에 따라 부호가 교대로 바뀌는(홀-음수, 짝-양수) n!이 된다.
원함수에다가 미리 -를 씌운 (-ln x)^n라고 해 주면 0..1 정적분은 간단하게 n!로 떨어진다. n이 홀수승일 때는 (ln x)^3의 값이 음수이던 것이 - 부호를 만나서 양수로 바뀌고, 짝수승일 때는 거듭제곱이 음수를 양수로 바꾸기 때문에 팩토리얼이 언제나 양수로 나오는 것이 보장된다.

로그의 거듭제곱의 적분이 팩토리얼과 관련이 있다니.. 신기한 노릇이다. 이 덕분에 지수뿐만 아니라 팩토리얼조차도 정의역이 단순히 자연수에 국한되지 않고, 지수함수와 적분와 동급인 실수 영역에 연속적인 형태로 정의될 수 있게 됐다.

(-ln x)^n의 0..1 정적분은 치환적분 기법을 동원해서 다음과 같은 형태로 바꿀 수 있다.

뭐.. 로그를 쓰면 구간이 0~1인데, 지수를 쓰면 구간이 0~무한대로 바뀐다는 차이가 있다. ㄲㄲㄲ
요 함수가 일명 '감마'(Γ) 함수라고 불린다. 단, 감마 함수는 모종의 이유로 인해 팩토리얼과 완전히 같지는 않아서 Γ(n+1)의 값이 n!에 대응한다.

x^x은 0일 때와 1일 때의 함수값이 동일하고, 그 사이엔 함수값이 살짝 작아졌다가 1 이후부터 폭발적으로 커진다.
감마 함수도 양의 실수 구간에서는 이와 비슷한 성질이 있어서 1과 2일 때의 함수값이 동일하다. 그 사이에는 함수값이 약간 작아졌다가 2 이후부터 폭발적으로 커진다.

단, x^x는 미분을 통해 그 최소값을 해석적으로 정확히 구할 수 있는 반면, 감마 함수는 대략 x≒1.46163에서의 최소값 0.88560...을 수치해석으로 구할 뿐이다. 이 수의 정확한 특성은 알려져 있지 않은 것 같다.
그런데.. 감마 함수는 소수점이 .5 인 수.. 다시 말해 자연수에다가 1/2이 첨가된 수에 대해서는 π(원주율)의 제곱근의 배수인 그 무언가를 되돌린다. 이런 것도 여느 지수함수나 그쪽 바리에이션에서는 발견할 수 없는 면모이다.

특히 Γ(1/2)의 값은 딱 정확하게 sqrt(pi)인데, 이것은 정규분포 함수의 원형인 e^(-x^2)의 전구간 적분 면적과 동일한 값이다.
1/2일 때 감마 함수 적분식은 적분변수 x를 sqrt(t)로 치환하면 딱 정확하게 e^(-x^2)의 전구간 적분과 동일한 식이 나오기 때문이다. ㅎㄷㄷㄷ..

물론 e^(-x^2)은 부정적분이 초등함수의 형태로 표현되지 않는 괴상한 물건이며, 가우스 적분이라는 완전히 새로운 방법론을 동원해야 전체 면적만을 구할 수 있다. 이 과정이 뱅그르르 회전과 관계가 있기 때문에 갑자기 원주율이 튀어나오는 것이다. 하지만 이건 이 글의 범위를 한참 넘어서기 때문에 더 자세한 얘기를 생략하겠다.

다시 본론으로 돌아오면.. 로그의 n승을 정적분 했더니 n팩토리얼이 튀어나왔다. 반대로 팩토리얼 값에 로그를 씌운 것도 로그와 관련이 있다. log N!은 수가 증가하는 정도가 N log N과 얼추 비슷하다.
왜 그런가 하면 N!은 1*2*3...*N이니 log N!은 log 1+log 2+log 3+ ...log N과 같기 때문이다. 그리고 이건 log N에 대한 적분에다 근사시킬 수 있으며, 그 부정적분에는 N log N이 포함되어 있다.

컴퓨터 알고리즘 중에서 정렬이라는 건 n개의 원소들을 나열하는 순열 최대 n!개의 가짓수 중에서 오름차순/내림차순 순서를 만족하는 것을 찾아내는 과정이다. 그런데 비교 연산을 한 번 할 때마다 그 가짓수를 이분 검색 하듯이 최대 절반으로 줄일 수 있다.

그러니 가짓수도 팩토리얼로 폭발적이고, 매 단계마다 가짓수를 줄이는 규모도 지수로 폭발적인데.. 결국 비교 연산을 수행하는 정렬 알고리즘의 이론적인 시간 복잡도는 팩토리얼의 로그급인 n log n으로 귀착되는 것이다.

팩토리얼 내지 팩토리얼의 로그를 근사하는 공식을 더 엄밀하게 파고들면 n log n에다가 다른 자잘한 항들도 여럿 붙는다. 이런 건 감마 함수를 변형해서 만들어지는데, '스털링의 근사 공식'이라고 한다.
애초에 x^n * e^(-x)도 e^(n ln x - x)로 바뀌니, n log n이라는 결론이 달라지지는 않는다.

이상이다. 로그에 이렇게 심오한 의미가 많이 담겨 있는 줄 몰랐다.;; 얘기가 꼬리에 꼬리를 물고 이어지는데, 로그의 밑 얘기만 하고 글을 맺도록 하겠다.

이공계에서 쓰이는 로그의 밑은 사실상 딱 세 종류.. 2, e, 아니면 10이라고 보면 되겠다.
2는 컴퓨터과학 전산학에서 특별히 아주 좋아하는 숫자이고, e는 지금까지 봐 왔듯이 천상 수학 미적분 해석학 전용이다. 10은 10진법과 관계가 있다 보니 데시벨이나 pH (산/염기 지수) 같은 로그 기반의 현실 과학 단위에서 쓰인다. 단, 복소해석학으로 가서 로그를 복소수 범위로 확장하면.. 0과 1만 빼고 -1이나 i조차 로그의 밑이 될 수 있으니 참 ㅎㄷㄷ하다.

현실에서 엄청 큰 측정값을 표기할 일이 있으면, 어지간해서는 메가· 기가· 테라· 페타 같은 접두사를 동원해서 자릿수를 줄이는 걸로 퉁칠 것이다. 아예 로그를 동원해서 자릿수를 후려친다는 건 정말 그 분야에서 얻을 수 있는 측정값의 스케일이 0의 개수 자릿수 차원에서 극단적으로 널뛰기 한다는 걸 뜻한다.

원래는 log 다음에 아래첨자로 밑을 일일이 써 주는 게 정석이다. 그러나 쓰이는 밑이 분야별로 저렇게 뻔히 답정너이니.. 그런 번거로운 표기는 잘 쓰이지 않는다. 밑이 e인 로그는 자연로그라고 해서 그냥 ln이라고 쓰는 정도?
밑을 생략한 log 표기는 밑이 무엇이건 중요하지 않고, 수가 증가하는 게 log 스케일이라는 것만이 중요할 때 쓰인다. 앞서 언급했던 시간 복잡도 표기처럼 말이다.

Posted by 사무엘

일반적인 수라는 건 제곱하면 값이 폭발적으로 커지거나(>1 발산), 반대로 0으로 급격히 오그라는 것으로 여겨진다.
다만, 1은 그 양극단의 딱 중앙에서 자기 형태가 변하지 않는다. 그리고 -1이나 i 같은 건 제곱하면 다른 수가 되었다가 도로 자기 자신으로 돌아오며 순환한다.

망델브로(만델브로트) 집합이라는 게, 0부터 시작해서 더하고 제곱, 더하고 제곱을 반복했을 때 발산하지 않는 복소수의 집합인 걸 생각해 보자. 꽤 오묘한 개념이다.
리만-제타 함수도 그렇고, 평범해 보이는 함수가 복소수 범위로 가면 난이도와 복잡도가 눈 튀어나올 정도로 치솟는 것들이 좀 있다. 제곱해서 -1이 되는 수를 하나 정의함으로써 사고 체계가 이 정도로 확장된다는 것이다.

수학이란 게 발명인지 아니면 발견인지에 대한 논쟁이 있다. 대부분의 업적들은 엄밀한 논리 체계를 찾아낸 발견에 가깝겠지만, 허수와 복소수는 아무래도 발명의 범주에 넣어야 할 것 같다. "제곱해서 -1이 되는 수도 있다고 가정해 보자" 이건 아무래도 자연 세계에서 존재하는 개념을 추상화한 건 아니니까 말이다.

복소수가 그런 것처럼 행렬도 발명에 가까운 도구가 아닐까 싶다. 그리고 가로와 세로 크기가 같은 정방행렬에 대해서는 거듭제곱을 생각할 수 있다.
행렬은 거듭제곱을 하면 행렬식 값도 거듭제곱 된다.
그런데 모든 원소가 몽땅 0이 아니어도 행렬식 값은 0일 수 있으며, 이로 인해 단독 숫자의 연산에서는 생각하기 어려운 특성이 존재할 수 있다.

제일 작고 단순한 2*2 크기의 행렬의 제곱은 일반적으로 다음과 같다.
[a b]^2 = [a^2+bc  b(a+d)]
[c d]     [c(a+d)  bc+d^2]

이를 토대로 이런 행렬을 생각해 보자.
2*2 행렬이란 게 원래 2변수 연립방정식을 푸는 도구인데, 얘 분석을 위해서 4변수 연립방정식을 풀게 생겼다.;;

1. 영행렬이 아니면서 제곱하면 영행렬이 되는 행렬

원소 중 적어도 하나 이상은 0이 아닌 행렬 중에 제곱 했을 때 완전 영행렬이 되는 행렬은 원소가 이런 꼴인 녀석이다. 요러면 제곱해 보면 모든 원소들이 x^2와 -x^2가 상쇄되는 식으로 소거되어 0이 된다.
[   x     y]
[-x^2/y  -x]

y가 원소 단독과 타 원소의 분모에 동시에 존재하니, 원소 중 하나는 반드시 nonzero여야 함이 보장된다.
이걸 전치시킨 것도 동일한 속성을 지니므로, nonzero 원소가 꼭 저 자리에만 있어야 할 필요는 없다.

y에다 1을 대입해서 식을 좀 간소화시키면 이런 형태가 되며..
[  t    1]
[-t^2  -t]

t에 1을 대입하면 일례로 요런 행렬이 나온다. 이런 게 제곱하면 영행렬이 된다는 것이다.
[ 1  1]
[-1 -1]

2. 영행렬이나 단위행렬이 아니면서 제곱하면 늘 자기 자신이 되는 행렬 (멱등행렬)

이건 프로그래밍 언어로 치면 자기 소스 코드를 그대로 출력하는 콰인 같은 느낌이다.;;;
사실은 너무 어렵게 생각할 것 없이, 단위행렬뿐만 아니라 거기서 숫자 일부를 0으로 바꾼 얘라든가, 0과 1이 일렬로 나란히 늘어서 있는 행렬도 다 멱등행렬이다.
[1 0]    [1 1]
[0 0] or [0 0]

이렇게 trivial한 경우 말고, 네 원소들이 모두 nonzero라고 가정하고 식을 세워 보면.. 반드시 a+d = 1이어야 한다는 조건이 먼저 나오고, 최종적으로 답이 이렇게 나온다.
[    x+1      y]
[-x*(x+1)/y  -x]

이런 행렬의 구성 원소는 아까 제곱-영행렬의 경우와 마찬가지로, 2개의 변수만으로 원소 4개의 값이 모두 결정됨을 알 수 있다. 또한, 오른쪽의 b와 d 원소를 동기화시켰을 때 a와 c는 저런 차이가 있다는 점이 매우 흥미롭다. 왼쪽에서 x가 x+1로 바뀐 정도의 차이가 전부이다. ㄲㄲㄲㄲ

저 식은 뭔가 미묘하게 규칙성이 있어 보인다. y=1인 경우만 생각해 보면 아래 row는 위의 row에다가 단순히 -x배를 한 것일 뿐이다. 예를 들어 이런 식이다.
[-2 1]    [ 2  1]
[-6 3] or [-2 -1]

그러니 행렬식 값은 당연히 0이다. 사실, 행렬식이 0이 아닌 멱등행렬은 단위행렬 단 하나밖에 존재하지 않는다.
이렇게 행렬식이 0인 2*2 행렬에다가 평면의 궤적을 선형변환 시키면, 평면도형을 일직선 위로 다 찌그러지게 된다. 제곱 결과물의 차이(영 또는 자기 자신)는 서로 다른 점조차 동일한 점에다가 겹쳐지는지 정도의 차이만을 만들 뿐이다.

제곱했을 때 특정 원소의 값이 확 커진다 하더라도, 행렬식이 0이면 그 일직선에서 엄청 먼 점까지 선형변환을 시킬 뿐, 일직선을 벗어나서 면적을 만들어 내지는 못한다. 이것이 이런 행렬이 갖는 대수적 의미이다.
3 이상의 더 큰 정사각행렬에서는 멱등행렬의 원소 관련 공식이 당연히 훨씬 더 복잡할 것이다. 그래도 규칙성은 갖추고 있을 것이다.

Posted by 사무엘

1. 수학
첫 5개인 3, 5, 17, 257, 65537은 소수라는 게 1600년대 사람인 페르마에 의해 밝혀졌다. 하지만 컴퓨터가 없던 시절이니, 그 뒤의 큰 수들도 모두 소수일지는 떡밥의 영역이었다. (17세기)

천문학
수 금 화 목 토성까지는 육안만으로 밤 하늘에서 관측 가능했기 때문에 아주 오래 전부터 알려져 있었다. 1600년대 사람인 갈릴레이 갈릴레오는 목성의 위성을 추가로 발견한 정도였다. (17세기)

2. 수학
65537 다음으로 4294967297 (약 43억ㅋ)은 641 * 6700417인 합성수임이 밝혀져서 페르마의 추측은 반증이 나와 버렸다. 컴퓨터가 없던 시절에 레온하르트 오일러라는 수학자가 무려 1732년에 겨우 20대 중반의 나이로 이걸 찾아냈다. (18세기)

천문학
천왕성은 1781년, 망원경 우주 관측 덕후이던 윌리엄 허셜에 의해 발견됐다. 태양계에서 발견자의 이름이 과학사에 기록돼 있는 가장 가까운 행성이 천왕성이다. 참고로 태양-토성 거리와 토성-천왕성 거리가 서로 비슷하다!
천왕성의 발견은 인류의 오랜 우주 식견을 확장시킨 위대한 발견이었다. 저 43억짜리 수를 소인수분해 한 것처럼 말이다. (18세기) 이건 답이 제안된 걸 검산하는 것만으로도 사람 손으로는 시간이 얼마나 걸릴까..?? ㄲㄲㄲ

3. 수학
2^32 +1 다음으로 2^64 +1은 이제 형언하기 어려울 정도로 큰 수이다. 오일러 이후로 100년이나 더 지난 1855년에야 얘 역시 합성수임이 밝혀졌다. (19세기)
발견자는 토머스 클라우센이라는 수학자인데, 아무래도 오일러보다야 훨씬 덜 유명한 사람이다.

천문학
천왕성 다음으로 해왕성은 1845~46년에 걸쳐서 마치 남침 땅굴 찾듯이 여러 학자들의 계산과 추적, 관측이라는 공동 기여를 통해 발견되었다. 천왕성처럼 근성가이가 망원경으로 하늘을 끈질기게 수색하다가 혼자 발견한 게 아니라는 뜻이다. (이쪽은 숨겨진 공동 기여라고 해 봤자 주변 가족 지인이나..)
그렇기 때문에 해왕성의 발견자는 천왕성의 발견자보다야 훨씬 덜 유명하다. (19세기)

4. 수학
페르마의 수 2^32 +1과 2^64 +1은 각각 F5와 F6에 대응한다. 얘는 2의 거듭제곱과 관련이 있다.

천문학
천왕성과 해왕성은 티티우스-보데의 경험 법칙에서 각각 6과 7에 대응한다. 이 법칙에서 제안하는 수식도 2의 거듭제곱이 들어있다.

5. 수학
F6은 컴퓨터가 발명되기 전에 인간의 수작업만으로 완전히 소인수분해를 해낸 가장 큰 마지막 수이다. 컴퓨터의 도움 없이 더 큰 페르마 수 몇 개가 합성수임이 증명된 사례가 있긴 하지만, 소인수분해를 몽땅 다 해서 증명한 건 아니었다.
F6 다음의 F7만 해도 전체 소인수분해가 완료된 때는 무려 1970년이었다! (20세기)

천문학
해왕성은 현재까지 태양계에서 알려진 마지막 행성이며, 티티우스-보데의 경험 법칙의 적중률도 한계에 도달하는 시점이다.
해왕성 다음으로 명왕성은 무려 1930년에야 발견됐다. (20세기)

6. 수학
페르마 수를 20번대 이후까지 찾아봐도 그 수들은 prime이 전혀 없이 모두 합성수였다. 페르마의 추측은 65537을 끝으로 더 적중하지 않았다.
그러니 후대의 수학자들의 견해도 점점 부정적 회의적으로 바뀌었지만.. 그렇다고 소수가 전혀 존재하지 않는다고 증명이 된 건 또 아니다. 난감한 지경이다.

천문학
명왕성은 2006년에 왜행성으로 강등 재분류됐다.
여기보다 더 먼 곳은 궤도가 너무 방대하고 태양의 인력도 너무 약하니, 뭔가 자기 궤도를 독차지하는 행성이 존재하기가 현실적으로 굉장히 어렵다. 관측하기도 난감하니 제9, 제10의 행성 떡밥은 가능성이 매우 낮다.

Posted by 사무엘

수학의 여러 분야에는 그 분야가 존재 가능한 이론적인 근간을 제공하는 '기본 정리'(fundamental theorem)라는 게 있다. 그 중 매우 대표적인 것은 다음 네 가지이다.

1. 산술의 기본정리(arithmetic)

모든 자연수는 유일한 소인수분해를 갖는다. 가령, 91이라는 수가 7*13이라는 수로 소인수분해가 된다면, 7과 13이 아닌 다른 소수의 곱으로 91을 만들 수 있는 가능성이 전혀 없다는 뜻이다. (가령, 근처의 비슷한 31*3으로는 93을 만들 수 있을 뿐..)
정리라고 할 것도 없는 너무 당연한 소리 같지만 RSA 암호화도 이런 기본정리가 성립하기 때문에 존재 가능하다는 걸 생각해 보자.

2. 선형대수의 기본정리

쉽게 말하면 선형 변환(linear transform)과 행렬은 표현 능력이 서로 동치라는 뜻이다. 전산학에서 "람다 대수와 튜링 기계는 계산 능력이 서로 동치이다" 이러는 것처럼 말이다.
이것도 그냥 당연한 말장난처럼 들리지만, 온갖 평행이동· 회전· 확대를 수반하는 복잡한 다단계 선형 변환을 몽땅 행렬의 곱으로 합성해서 한꺼번에 간편하게 짠~ 할 수 있는 이론적 근간이 바로 이 기본정리이다.
여기 하위 범주로 가역행렬의 기본정리라는 것도 있다.

3. 대수학의 기본정리(algebra)

일변수 n차 방정식은 복소수 범위에서 적어도 1개 이상, 최대 n개의 근이 존재하는 것이 언제나 보장된다. 즉, 복소수라는 '체'(field)는 대수적으로 닫힌 체이다.
2차 방정식의 근을 허근까지 일관되게 온전히 표현하기 위해서, 허수와 복소수라는 개념이 처음 도입됐다. 하지만 그 이상 100차 방정식의 근을 구해서 표현하기 위해서, 혹은 제곱해서 i가 되는 수를 표현하기 위해서 수 체계를 그런 식으로 매번 또 확장할 필요는 없다는 것이 이 기본정리의 핵심이다. 복소수만으로 족하다~!! 이건 굉장히 위대한 업적이다.

4. 미적분의 기본정리(calculus)

(1) 적분은 미분의 역연산 관계이다~!! 이건 서로 다른 기원에서 출발한 지수와 로그가 한데 만나고, 물리에서 전기와 자기가 한데 만나서 전자기학이 된 것과 같은 엄청난 발상의 전환이 됐다.
그리고 (2) 구간 정적분 값은 부정적분의 끝점값과 시작점의 차이를 통해 아주 '간편하게' 구할 수 있다.
배배 꼬아 놓은 복잡한 미적분 문제 끌어안고 끙끙대기 전에 한번쯤.. 도대체 어떻게 해서 이 엄청난 일이 가능한지 생각을 좀 하고 곱씹을 기회가 있어야 학교 수학 시간이 덜 괴로울 것이다.

교회에서 배운 '일곱 침례, 일곱 심판, 다섯 왕관' 이런 게 떠오르더라.
요한의 침례, 회개의 침례, 물 침례, 불 침례 등등..
그리고 생명의 왕관, 썩지 않을 왕관, 환희의 왕관, 의의 왕관 등등..처럼.
수학에 기본정리가 분야별로 몇 가지가 좀 존재하듯 가끔은 성경도 좀 이꽈 마인드로 엄밀하게 접근하고 분류· 분석하고 파고들 필요가 있다. 온갖 무질서와 혼돈을 예방하려면 말이다.

• i로도 모자라서 j, k 까지 갖다붙인 사원수라는 것도 있다. (서로 모두 다른 세 수 i,j,k가 존재하여 i^2 = j^2 = k^2 = ijk = -1인 체계. 마치 행렬처럼 곱셈의 교환 법칙이 성립하지 않음) 하지만.. 이건 대수적인 필요에 의해 만들어진 수 체계는 아니다.
• 수학에서는 유한 번이냐 무한이냐를 따지지만, 전산학에서는 컴퓨터의 계산 성능을 현실적으로 감안하여 다항함수(polinomial) 시간이냐 지수함수 시간이냐를 따지는 편이다.

* 수와 함수

정수/유리수 계수 방정식의 근이 될 수 있는 수를 '대수적인 수'라고 하고, 그렇지 않은 수를 초월수라고 부른다. 그런데 5차 이상의 방정식의 일반해는 분명 복소수의 범위를 벗어나지 않고 대수적인 수이기까지 함에도 불구하고 유한 번의 사칙· 거듭제곱· 제곱근 조합으로 표현할 수 없다.
이는 정말 기괴하고 독특한 성질이다. 단순히 지수함수 수준으로 미치도록 복잡해지기만 하는 게 아니라 "답이 아예 없음. 절대 불가능"이 되는 것이다.

함수도 다항함수나 유리· 무리함수를 넘어서 지수· 로그· 삼각함수 같은 것들은 유리수(특히 정수가 아닌..)를 집어넣었을 때 어지간하면 다 초월수가 튀어나오기 때문에 '초월함수'라고 불린다. 그런데 고등학교 수준의 저런 함수들은 비록 초월함수이지만 해석학의 관점에서는 e^x 어쩌구에서 크게 벗어나지 않는 친근(?)한 놈들인 관계로.. '초등함수'라고 해서 별도로 분류된다.

부정적분은 미분과 달리 '초등함수'에 대해 닫혀 있지 않다. x^x나 e^(x^2) 같은 함수만 해도.. 미분과 달리 부정적분은 기존 초등함수들의 조합이나 사칙연산 합성으로 표현할 수 없는 형태가 나온다.
이건 대수적인 수가 기존 산술 연산에 대해 닫혀 있지 않은 것처럼 아주 신기한 면모이다.

* 방정식

방정식은 미지수의 성격 내지 풀이 방법론에 따라 다음과 같이 범주가 나뉜다.

• 일변수 n차 대수: 앞서 대수학의 기본정리에서 언급한 바로 그놈이다. 변수는 하나인데 그 변수가 스스로 곱해질 수 있다.
  다항식 형태가 아닌 유리· 무리방정식은 양변을 적절히 곱하고 나눠서 다항식 형태로 변형한 뒤에 푸는데, 이것들은 애초에 다항식이 아니기 때문에 다항식 변형 버전에만 존재하는 무연근을 걸러 줘야 된다.
• 다변수 연립: 차수는 높지 않은 대신, 변수와 식이 많은 동네이다. 변수와 식이 하나 추가될 때마다 식을 분석하는 원론적인 시간 복잡도는(행렬식의 일반항) 팩토리얼 급으로 복잡해지고, 실용적으로 문제를 푸는 복잡도는 행렬의 곱셈에 준하는 3제곱으로 증가한다.
• 점화식: 재귀적으로 정의되는 식의 일반항을 구하는 문제인데.. 이것도 항이 하나 늘어날 때마다 특성방정식의 차수가 하나씩 올라가고 복잡도가 급격히 올라간다.
• 미분방정식: 연속적인 물리량의 변화를 중요하게 따지는 공대에서 매우 중요하게 다루는 도구이다. 어떤 함수의 부정적분, 즉, 역도함수를 구하는 문제부터가 아주 기초적인 미분방정식을 푸는 것과 같다. 그런데 이것도 해석적으로 정확하게 풀 수 있는 문제가 별로 없고 극도로 어렵다.

방정식의 바리에이션으로는 이런 것들이 있다.

(1) 부등식: 방정식 풀듯이 풀면 되는데, 여기서는 부등호의 방향을 좀 생각해야 한다. 그리고 부등식은 그 특성상 복소수는 생각하지 않고 도메인이 다시 실수로 좁아진다.
방정식 동네에 상호 동치를 나타내는 항등식이라는 게 있다면, 부등식 동네에는 어떤 수를 넣어도 성립하는 절대부등식이라는 게 있다. 중등 수학 수준에서는 코시-슈바르츠 부등식이라든가 산술-기하-조화평균 부등식이 유명하다.
다변수 연립으로 있는 부등식을 푸는 건 최적화와 관련하여 실용적으로도 매우 중요한 문제이다.

(2) 합동식: 여기는 범위를 실수보다도 더 좁혀서 자연수만 상대하는 동네이다. 어떤 수로 나눈 나머지가 같은 수들을 합동이라고 간주하면서 여기만의 굉장히 복잡한 조건을 만족하는 수를 찾는다. 이건 정규 교육과정에서 다루지 않고 공대에서도 딱히 다루지 않기 때문에 수학 올림피아드 하는 애들의 전유물이다.

다음 둘은 영역이 서로 별개이지만, 둘 다 끔찍하게 어려우며 대수적으로 정확한 일반해를 구할 수 없는 문제라는 공통점이 있다.

• 공기가 있는 곳에서 비행체의 운동을 기술하는 나비에-스토크스 방정식..
• 공기가 없는 곳에서 천체의 운동을 기술하는 3체/다체 문제..

전자의 경우 수치해석이나 시뮬레이션, 심지어 풍동 실험실이 여전히 유효한 지경이다.
후자는.. 우주에서 일부 듣보잡 소행성들이 깔끔 단순한 원뿔곡선이 아니라 훨씬 더 복잡하고 꼬불꼬불하고 무질서한 궤도를 그리는 이유가 이 때문이다.

Posted by 사무엘

자동차가 나아가면서 그리는 궤적은 직선 아니면 원호이다. 핸들을 꺾은 채로 가만히 있으면 좌우 어디로든 원호 궤적을 그린다.
그렇기 때문에 도로의 커브 역시 이런 모양을 염두에 두고 설계된다. 고속도로는 커브의 회전 반경이 더 크다. 하지만 직선과 원호만이 궤적의 전부가 아니며, 그 중간 단계에 속하는 궤적도 쓰인다.

그것은 바로 클로소이드(clothoid curve)이다. 얘는 정속 주행하면서 핸들을 일정한 각속도로 돌릴 때 차량이 그리는 궤적이다.
핸들이 돌려져 있긴 하지만 그 각의 변화가 없는 채로 차가 정속 주행하면 잘 알다시피 원호가 그려진다. 그러나 그 곡률도 일정하게 변하면 저런 더 복잡한 곡선이 나온다는 것이다. 간단히 코딩을 해서 궤적을 그려 볼 수도 있다.

차를 몰고 이런 커브를 돈다고 생각해 보자. 핸들을 서서히 더 꺾어야겠다는 생각이 절로 들 것이다.
이 궤적은 보다시피 각에 정비례해서 중심으로부터의 거리를 일정하게 줄였을 때 나오는 소용돌이 궤적과는 다르다. 매개변수를 통해 수학적으로는 이렇게 표현된다고 한다.

원호라면 [cos(t), sin(t)]라고 너무 간단하게 표현되겠지만, 움직이는 동안 각도가 계속 변하다 보니 식이 저렇게 이상하게 바뀌었다.
극좌표로는 어째 표현할 방법이 없는가 모르겠다. 원호는 아예 상수가 되어 버리는데 말이다. 다만, 얘는 직교좌표에 친화적인 직선과도 접점이 있는 물건이기 때문에 극좌표를 동원한다고 해도 더 간편· 간단한 형태가 나오지는 않을 것 같다.

cos(x)^2가 아니라 cos(x^2)라는 걸 유의하시라. 이건 고등학교 수준의 삼각함수 덧셈 정리의 제곱 법칙 등으로도 전혀 요리할 수 없다. 저 함수의 부정적분은 같은 초등함수들의 조합으로 나타낼 수 없다.

이 궤적은 그래도 중심점에 완전히 붙어 버리지는 않고 뱅글뱅글 돌게 된다는 게 특징이다. 그래도 현실의 자동차는 핸들을 무한히 꺾을 수 없기 때문에 도로에서는 이 궤적의 극히 일부만을 이용해서 직선과 원호를 연결하게 된다. 이런 식으로 말이다.

직선과 원호만 적절히 연결해도 수학적으로는 연속이고 미분 가능한 궤적이 나온다. 하지만 그걸로 충분치 않아서 운전자가 핸들을 돌리는 속도까지 감안한 완화 곡선이 쓰인다는 게 신기하지 않은가?
이 개념은 심지어 핸들이라는 게 존재하지 않는 철도에서도 예외 없이 쓰인다. 그래서 R=400, R=3000짜리 커브라고 해도 그 지도에다가 반지름이 그만 한 원을 그려 봐도 철길의 선형은 그 원보다 훨씬 더 완만해 보인다.

이게 천체의 운동이나 우주 탐사선의 궤적을 기술하는 식과 접점이 있으려나..?? 당장 사고실험을 해 봐도 그건 운동하는 방식이 완전히 다른데 같을 리가 없어 보인다. 하지만 심상이 서로 미묘하게 비슷해 보인다.

이렇듯, 몇백 년 전에 유럽의 수학자들은 자연과 일상생활에서 발생하는 어지간한 운동들을 몽땅 다 미적분 해석학으로 기술해 냈다. 예전에 다뤘던 사이클로이드, 현수선 같은 것 말이다. 그것도 컴퓨터나 계산기가 없던 시절에 머리와 종이만으로 증명을 해 내다니.. 생각하면 생각할수록 경이롭다.

Posted by 사무엘

두 초점 A, B가 있을 때 A에서의 거리와 B에서의 거리의 차가 동일한 점들의 집합을 쌍곡선이라고 한다. x^2 - y^2 = a 이런 음함수로 정의되며, 그래프를 그려 보면 곡선이 둘 그어지는 것이 특징이다.
그 반면, 합이 동일한 점들의 집합은 잘 알다시피 타원이며, x^2 + y^2 = a 꼴로 정의된다.

그런데 y=a/x, 다시 말해 xy = a 꼴인 반비례 함수는 x^2나 y^2처럼 단일 변수의 제곱이 존재하지 않는다. 하지만 우리는 이게 이차곡선인 쌍곡선의 표준형을 45도 돌린 형태라고 얼추 알고 있다.
어째서 그런 것일까? 수학적으로 더 엄밀히 증명해 볼 수는 없을까?
반비례 함수를 회전 행렬을 이용해서 45도 돌린 뒤, 이 함수가 쌍곡선 표준형과 동치임을 보이면 될 것이다.

45도일 때는 cos와 sin의 값이 sqrt(2)/2로 동일하다. 그렇기 때문에 (x, y)라는 점은 45도 회전하고 나면

요렇게 된다. 그럼 다음으로 45도 돌아간 x', y'를 기반으로 우리의 목표인 쌍곡선 방정식을 재구성하면 된다.
그러면 기존의 x, y 변수를 없애야 하는데, 위의 식을 그대로 제곱해서 빼기만 해도 x'^2 - y'^2 = -2xy로 놀랍게도 x^2와 y^2이 소거되어 없어진다. 이는 앞서 살펴보았듯이 각도가 45도여서 cos와 sin의 함수값이 서로 동일한 덕분에 가능한 일이다.

마지막으로 남은 xy야 원래 반비례 그래프의 정의상 a로 치환하면 되니 금방 처리된다.
그러면 x'^2 - y'^2 = -2a가 되고 쌍곡선과 동일함이 입증된다. 뭔가 허무해 보이지만.. 이차곡선 중에서 x나 y의 제곱이 없는 식은 이렇게 쌍곡선으로 귀결된다.
45도가 아닌 다른 각도라면 기존 x, y가 이렇게 쉽게 소거되지 않기 때문에 문제가 이런 식으로 단순하게 풀리지 않게 된다.

가만히 생각해 보니, 애초에 Ax^2 + Bxy + Cy^2 + Dx+Ey+F = 0에 대해서 그래프의 모양을 결정하는 판별식도 있다. A,B,C 중 적어도 하나 이상은 0이 아닐 때, B^2 - 4AC가 0이면 이 그래프는 포물선이요, 음수이면 타원 또는 원, 양수이면 쌍곡선이 된다. 구체적인 유도 과정은 쉽지 않을 텐데.. 이거 정도면 중등 교육과정 범위에 있다.
그러니 xy=1이야 B만 비영이고 A, C는 0.. 판별식 값은 당연히 양수가 되고 쌍곡선으로 귀결된다. 오오~~

판별식의 형태가 1계수 이차방정식의 근 판별식과도 매우 유사하다. 이차방정식의 경우 A만 비영이라는 조건이지만, 이차곡선 내지 원뿔곡선 방정식의 판별식은 아까 상술하였듯이 A,B,C 중 아무거나 하나 이상만 비영이면 된다.

그리고 A부터 F까지 아무 숫자나 집어넣는다고 해서 원뿔곡선이 튀어나오는 게 아니다. 상수항이 0이거나 하면 원이 극도로 작아져서 그냥 점이 되기도 하며, 쌍곡선은 점근선을 나타내는 직선 두 개로 귀착된다. 당장 xy=0만 해도 x축과 y축을 동시에 나타나내는 직선이 되니까.. 그럼 다음으로 포물선은..? 평행한 두 직선이 돼 버린다.
이차방정식이 x^2+1 = 0 같은 경우 실수 근이 존재하지 않는 것처럼.. 이것의 이변수 상위 호환인 원뿔곡선 방정식도 실수 범위에서 공집합이 될 수도 있다.

이 개념을 degeneracy(축퇴.. 축 쪽으로 퇴화)라고 부른다. 뭔가 행렬에서 행렬식의 값이 0이 돼 버리는 상황 같은 느낌이 들지 않는가? 계수가 주어졌을 때 축퇴 여부를 판별하는 판별식도 있다. 이건

(b^2-4ac)f + ae^2 - bde + cd^2

으로, 곡선 종류 판별식을 포함하면서 다소 복잡한 편이다. 이걸 유도하는 건 확실하게 중등 이상의 더 어려운 영역이며, 더 추상적인 수학 개념이 동원된다. 딱 봤을 때 각 항들에 변수가 2개가 아니라 3개씩 곱해진 것부터가 매우 인상적이다.

쌍곡선에서 시작해서 이차곡선에 대한 더 원론적인 얘기로 주제가 옆길로 좀 샜는데.. 다시 쌍곡선 얘기를 하며 글을 맺겠다.
반비례 그래프는 xy=a, 즉 x의 역수를 구하는 함수인지라 y=-x의 그래프에 대칭인 쌍곡선이 튀어나온다. e^x가 도함수가 자신과 동일한 함수라면, a/x는 역함수가 자신과 동일한 함수이다. f(f(x)) = x가 성립하는 게 어찌 보면 not이나 xor 연산 같아 보이기도 하다..

원의 방정식이 그 정의상 (cos(t), sin(t))라는 매개변수로 표현될 수 있는 것처럼 쌍곡선의 방정식은 (cosh(t), sinh(t))라는 매개변수로 표현될 수 있다. cosh와 sinh의 배치가 바뀌면 쌍곡선의 위치가 상하 또는 좌우로 바뀐다.

그리고 원의 방정식이 y=sqrt(a-x^2) 같은 꼴로 양함수로 표현될 수 있는 것처럼 쌍곡선의 방정식은 y=sqrt(x^2+a)의 꼴로 표현될 수 있다. a의 부호가 무엇이냐에 따라 쌍곡선의 배치(상하 또는 좌우)가 바뀐다. 한편으로 저 모양만 봐도 x의 값이 너무 작거나 커지면 y=x에 가까워질 소지가 다분해 보임을 알 수 있다.

Posted by 사무엘

피보나치 수열이란 첫 두 항 F(1)와 F(2)의 값이 1이고, 그 다음부터는 n>=3인 자연수에 대해 F(n) = F(n-1)+F(n-2)이라고 재귀적으로 정의되는 수열이다.
1, 1, 2, 3, 5, 8, 13, 21, 34 …와 같은 순으로 숫자가 나열되며, 수가 커질수록 인접한 두 항의 비율은 황금비 (1+sqrt(5))/2로 수렴한다. 즉, 얘는 1 2 4 8 같은 등비수열과 동일한 형태는 아니지만, 수가 증가하는 정도가 등비수열과 동급이다.

그런데 다른 F 값에 의존하지 않고 F(n)의 값을 곧바로 구할 수는 없을까? 다시 말해 F(n)의 일반항을 구할 수는 없을까?

결론부터 말하자면.. 구할 수 있을 뿐만 아니라 더 나아가 0이 아닌 아무 a,b,c와 초기값 F(1), F(2)에 대해서 a*F(n+2) + b*F(n+1) + c*F(n) = 0꼴의 점화식 자체의 일반항을 구하는 것도 가능하다.
저런 점화식의 일반항은 X^n ± Y^n 의 형태로 귀착된다(X, Y는 임의의 상수). 피보나치 수열은 저기서 a=1이고 b=c=-1, F(1)=F(2)=1인 경우일 뿐이다.

이 점화식을 푸는 것의 핵심은 점화식을 동일하게 유지하면서 기존 a, b, c 계수를 각각 1, -(p+q), p*q라는 형태로 바꾸는 것이다. a는 a, b, c를 똑같이 a로 나눠 주면 1로 바꿀 수 있고, b와 c는 합이 -b이고 곱이 c인 p, q라는 또 다른 숫자쌍을 구해서 바꾸면 된다. 이런 식으로 일반성을 유지하면서 계수의 형태를 치환하는 건 3차나 4차 같은 대수방정식을 풀 때도 볼 수 있는 테크닉이다.

계수의 형태를 저렇게 바꿈으로써 우리는 동일한 점화식을 F(n+2) - p*F(n+1) = q*( F(n+1) - p*F(n) )이라고.. 우리가 처리하기 더 유리한 단순한 형태로 변형할 수 있다. 어떤 점에서 더 유리한지는 곧 알게 될 것이다.
p와 q 둘 중 하나가 0이면 F(n)은 그냥 평범한 등비수열이 되겠지만, 단서가 더 추가됨으로써 변형이 가해진 좀 더 복잡한 수열을 만들 수 있다.

가령, F(1)=F(2)=1이면서 p=2, q=-1이면 이 수열은 1 1 3 5 11 21 43 ... 즉, 앞의 수의 2배에다가 1을 더하거나 뺀 형태가 되며,
p=3, q=-2이면 1 1 7 13 55 133 463 1261 ... 앞의 수의 3배에다가 각각 4, -8, 16, -32를 더한.. 기묘한 수열이 만들어진다.

이런 유형의 수열을 저 점화식으로 표현할 수 있다는 것이다. 그리고 피보나치 수열은 p+q=1, pq=-1인 경우이다.
(그러고 보니 다른 수학 교재에서는 이때 p, q 대신 알파와 베타를 쓰는 편이더라만.. 그건 그냥 기분과 취향 문제이니 이 글에서는 계속해서 p, q를 쓰도록 하겠다.)

F(n+2) - p*F(n+1) = q*( F(n+1) - p*F(n) ) 이라는 식을 잘 살펴보면.. 그 정의상 초기항인 F(2) - p*F(1)에다가 q를 곱해 주는 것만으로 F의 등급을 쭉쭉 올릴 수 있다. 무슨 얘기냐 하면, n>=1에 대해서 F(n+2) - p*F(n+1) = q^n * (F(2) - p*F(1))이라는 것이다. 이런 놀라운 특성 때문에 점화식을 이런 형태로 바꾼 것이다.

저렇게 하면 식의 우변이 p, q, F(1), F(2)라는 상수 형태로 완전히 바뀐다. 아, 우변이 F(n)에 대한 의존도만 없어졌지 n에 대한 지수함수이기 때문에 완전한 상수는 아니다. 완전한 상수라면 이 형태만으로 문제가 다 풀렸을 것이다.
이 상태에서 식을 더 단순화시키기 위해서 우리가 활용하는 특성은 바로.. p, q의 값이 서로 뒤바뀌어도 생성되는 순열 결과는 달라지지 않는다는 것이다.

애초에 덧셈과 곱셈은 교환 법칙이 성립하는 연산이다. 그러니 p, q의 등장 순서를 뒤바꿔도 합 -b와 곱 c는 바뀌지 않을 것이다. 위의 점화식을 F(n+2) - q*F(n+1) = p*( F(n+1) - q*F(n) ) 이라고 바꿔 줘도 달라지는 것은 전혀 없다.

기하학적으로 생각하자면 저건 쌍곡선(곱이 같음 = 반비례)과 직선(합이 같음 = 정비례)의 교점을 구하는 것과 같다. 그 직선이 쌍곡선의 점근선 중 하나와 수직-평행 관계가 아닌 한, 교점은 “둘” 존재하게 될 것이다.

대수적으로 생각한다면야 저건 평범한 이차방정식을 푸는 것과 같다. -(p+q)와 p*q는 이차방정식 (x-p)(x-q)와 정확하게 대응한다. (x-p)(x-q)를 하든 (x-q)(x-p)를 하든 식이 달라지는 것은 없다. 너무 당연한 얘기이다.

F(n+2) - p*F(n+1) = q^n *( F(2) - p*F(1) )
F(n+2) - q*F(n+1) = p^n *( F(2) - q*F(1) )

그래서 위의 등식에서 아래의 등식을 그대로 빼 버리면.. F(n-2)가 없어지고 등식 전체에서 F(n+1) 하나만 남게 된다.
F(n+1)의 앞에 붙은 q-p라는 계수로 양변을 나누고, n을 n-1로 치환하면 일반항 유도가 완료된다. 대략

F(n) = ( (q*F(1) - F(2))*p^(n-1) - (p*F(1) - F(2))*q^(n-1) ) / (q-p)

라는 비교적 깔끔한 식이 나온다. 이 정도는 심하게 복잡하지는 않으니 이미지 대신 그냥 문자 형태로 때웠다. ㄲㄲ
양변을 덧셈이 아니라 뺄셈을 했기 때문에 F(1)과 F(2)의 부호가 반대로 바뀌었다.

피보나치 수열의 일반항은 저기에서 F(1)=F(2)=1, 그리고 p와 q에다가는 x^2 - x - 1 = 0의 근인 (1+sqrt(5))/2와 (1-sqrt(5))/2를 각각 대입하기만 하면 구할 수 있다.
번거로운 계산이 많긴 하지만 F(n) = (p^n - q^n)/(p-q)의 형태가 된다. 형태가 꽤 복잡해 보이는데, 그래도 n에다가 자연수를 대입해 보면 근호(루트)는 거짓말처럼 없어져서 최종 결과값이 자연수로만 딱딱 떨어진다.
분자의 거듭제곱은 그렇다 쳐도 분모는 p-q는 sqrt(5)로 깔끔하게 나오기 때문에 표기가 그리 복잡하지 않다.

이상이다. 글을 쭉 쓰면서 본인도 이 분야에 대한 공부를 확실하게 다시 할 수 있었다.
메이플이나 매스매티카 같은 수학 패키지에는 점화식을 푸는 명령이 물론 존재한다.
F(x+2) - (p+q)*F(x+1) + p*q*F(x) = 0의 일반항은 단순무식 F(x+2) + b*F(x+1) + c*F(x) = 0 보다 훨씬 더 간단하게 나오는 걸 알 수 있다. 후자는 내부적으로 sqrt(b^2-4*c) 같은 근의 공식이 잔뜩 섞여서 매우 복잡하다.

그리고 끝으로 생각할 점은..
피보나치 수열 정도는 이전 항의 이전 항.. 즉 2단계까지 역참조하는 점화식인데, 그 단계가 3단계 정도로만 올라가도 식의 복잡도는 상상 이상으로 치솟을 거라는 점이다. 특성 방정식은 2차가 아니라 3차가 될 것이고, 변수들을 연립해 주는 식도 2차가 아닌 3차가 될 것이고.. 실용적인 방법으로 일반항을 구하는 게 도저히 가능하지 않겠다.

Posted by 사무엘

이제 우리는 오일러 방정식 말고 다른 방식으로도 사이클로이드의 최단 강하 성질을 유도해 보고자 한다.
이것은 뉴턴 말고 동시대의 다른 천재 과학자이던 요한 베르누이가 최초로 발견했다.

물리 과목이 고전역학과 유체역학, 열역학, 전자기학을 넘어 파동과 입자 파트로 넘어갈 즈음에, 우리는 스넬의 법칙이란 걸 접하게 된다.
빛이 한 매질 속에서 v1이라는 속도로 나아가다가 속도가 다른(v2) 매질로 진입했을 때 잘 알다시피 굴절이 발생하는데.. 그 굴절 각도 사이에

sin θ1 : v1 = sin θ2 : v2

비율이 동일하게 유지된다는 법칙이다.
물리학이라는 게 딱딱한 물체의 가시적인 움직임만 기술하는 줄 알았는데.. 물 속에 비치는 물체가 실제보다 얕게 보이는 이유와 정확하게 얼마나 얕게 보이는지까지 수식으로 알려준다는 것이 경이롭다. 이건 게임에다 비유하자면 말 그대로 오브젝트들의 운동 역학뿐만 아니라 그래픽 렌더링에까지 관여한다고 볼 수 있다.

뭐, 0도~90도 사이에서 sin x는 x 자체와 별 차이 없을 정도로 단조증가만 하니, 위의 법칙이 아주 특이한 결과를 만들지는 않는다. 빛의 속도가 빠른 곳에서는 각도가 작아지고, 느린 곳에서는 각도가 대체로 커진다. 단지 고각이 될수록 그 정도에는 선형적이지 않은 차이가 발생할 뿐이다.
(낮은 각도에서 x와 sin(x)는 그리 크게 차이가 나지 않는다는 점은 단진자 주기의 근사값을 구할 때도 쓰인다. 이에 대해서는 곧 다시 다루어질 것이므로 참고하시라.)

그런데 빛은 애초에 질량이 없는 물건이고 구슬처럼 데구르르 구르지도 않을 텐데 저 법칙이 사이클로이드 내지 최단 강하 곡선과 무슨 관계가 있는 걸까..??
고지대는 매질이 진해서(...;) 빛의 속도가 제일 느리고, 아래로 갈수록 점진적으로, 선형적으로 매질의 농도가 옅어져서 빛이 더 빠르게 진행할 수 있다고 가정해 보자. 이게 빛에게 중력 역할을 하는 거나 마찬가지이다.

다시 말해, 공기 아니면 물 같은 이산적인 흑백이 아니라, 그러데이션을 생각하면 된다.
이런 상황을 만들어 놓고 위에서 아래로 빛을 조금이라도 비스듬하게 쏘면.. 빛 역시 단순무식하게 직선 형태로 나아가지 않게 된다. 최고 속도를 낼 수 있는 방향으로 쭈루룩 휘어지고, 그 궤적이 놀랍게도 사이클로이드가 된다.

즉, 궤적의 어느 점에서나, 어느 높이에서나 sinθ / v의 값은 일정해야 한다.
출처에 따라서 sinθ / sqrt(h) = C(상수) 라고 표기하기도 한다. 앞서 값을 구한 바와 같이, 속도 v는 sqrt(2*g*y)로, 높이의 제곱근에 비례하기 때문이다. y축이나 높이 h나 동일한 개념인 것은 다들 아실 테고..

그리고 여기서 각도 θ라는 건 보다시피 y축(세로선) 기준의 값이다. 이를 x축 기준으로 환산하면 90도-θ나 마찬가지이다. 즉, y축 기준 입사각 90도는 x축 기준 0도와 같다는 뜻.. 그러므로 y축 기준으로 sin θ는 우리 입장에서는 cos θ와 같은데..;;

여기서 놀라운 발상의 전환이 가능하다.
cosθ는 1/sqrt(tan(θ)^2 + 1) 로 형태를 바꿔치기 할 수 있다! (sinθ^2 + cosθ^2 = 1이니까)
여기서 탄젠트라는 건? 고맙게도 x축 대비 y의 변화량.. dy/dx, 다시 말해 y' 그 자체이다.

그러므로 sinθ/v에서 분자는 1/sqrt(1+y'^2)로 깔끔하게 나왔고, 분모 v에다가는 sqrt(2gy)를 집어넣으면..
이게 곧 미분 방정식

1/( sqrt(2gy)*sqrt(1+ y'^2)) = C

이 나오는데, 이건 앞서 오일러-라그랑주 방정식에서 d/dy 안에다 대입해서 집어넣었던 ∂F/∂x'와 같은 형태이다. 그때는 x를 먼저 구했지만 지금은 y를 먼저 구할 뿐... 그리고 그때도 지금처럼 y를 먼저 구하는 식으로 풀 수 있다.

잡다한 상수와 근호를 치우고 식을 정리하면 y(1+y'^2) = C 를 얻는다.
제곱이 좀 압박스럽게 보이긴 하지만, 얘는 dx = dy sqrt( y/(C-y) ) 로 변형 가능하며 이건.. 역시 이전 방식에서 얻었던 x'의 형태와 같다.
그러니 y를 삼각함수의 제곱으로 치환해서 계속 풀어 나가면 된다. 이상.. 더 이상의 자세한 설명은 다른 참고 사이트에서 열람하시기 바란다. (☞ 참고 1, 참고 2)

사이클로이드는 공대 1학년의 기초 필수 코스인 벡터 미적분학 교육과정에서 정말 최고로 적합한 교보재인 것 같다.
스넬의 법칙 덕분에 풀이의 일부가 좀 간소화된 듯한 느낌인데.. 사실 스넬의 법칙도 직접 유도해 보면 물리에 앞서 오일러-라그랑주 방정식과 동급의 수학 원리가 이미 깔끔하게 담긴 것이나 마찬가지이다.

빛이 속도를 최대화하기 위해 사이클로이드 궤적 형태로 굴절된다니, 이건 우주 로켓 발사와도 동일하지는 않지만 비슷한 구석이 있어 보인다.
공기가 가장 짙고 공기 저항도 극심한 지상에서는 이 구간을 빨리 빠져나가는 게 중요하므로 로켓이 닥치고 수직 상승한다. 하지만 공기가 충분히 옅어지면 이제 수평으로도 속도를 내서 지구 궤도에 진입할 채비를 하니까 말이다.

그렇게 각 고도별로 수직과 수평 동력을 잘 배분하여 연료를 가장 적게 쓰고 궤도에 진입할 수 있다. 그리고 그 경로를 짜는 건 굉장한 노하우가 필요하다. 여기에도 사이클로이드 궤적이 쓰이는지 궁금하다.

2. 등시 곡선

아이고 힘들다.. 최단 강하 곡선 얘기가 이렇게 길어질 줄 몰랐네.. 그런데 이게 사이클로이드의 역학적 특성의 끝이 아니다.
얘는 최단 강하 곡선인 동시에 놀랍게도 ‘등시 곡선’이기도 하다.
무슨 말이냐 하면.. 공을 곡선의 맨 꼭대기에서 굴리든, 밑바닥 근처에서 살살 굴리든, 목적지인 밑바닥에는 동일한 시간 후에 도착한다는 것이다! (공기 저항과 마찰을 무시하는 한)

이 말을 들으면 같이 떠오르는 게 있다. 바로 단진자의 운동.
학창 시절에 배운 기억으로는 단진자도 각도라든가 추의 무게와 무관하게 왕복 주기가 동일하다. 오로지 실의 길이 l과 중력가속도 g의 영향만 받아서 2π*sqrt(l/g)라는 공식이 나왔었다. (줄 길이의 제곱근에 비례)

그런데 공중에 대롱대롱 매달린 단진자가 그리는 궤적은 사이클로이드가 아니라 그냥 원호이다. 둘이 어떻게 동일할 수가 있지?
관련 자료를 다시 찾아보니, 단진자의 주기는 각도와 완전히 무관한 게 아니었다. 중등 수준에 맞게 난이도 보정을 하느라 θ가 충분히 작아서 sinθ가 θ와 얼추 같다고 “치고” 식을 유도한 것이었다. 원래 미분방정식은 θ'' + sinθ *g/l = 0 이렇게 나오는데, sinθ를 놔두면 미분방정식이 너무 어렵고 복잡해지기 때문이다.

언젠가 물리 시간에 뭔가 “sinθ가 θ와 얼추 같다고 치고” 식을 유도하는 걸 접한 기억은 있지만 그게 단진자 주기 공식이었다는 건 오랫동안 잊고 있었다.
sinθ를 살려서 문제를 해석학적으로 정확하게 풀려면 타원 적분이란 걸 동원해야 하며, 최종적인 답이 무한급수의 형태로 튀어나오게 된다. 이런 복잡한 항들이 2π*sqrt(l/g)의 뒤에 덕지덕지 추가적으로 곱해진다. 자세한 것은 타 사이트의 설명을 참고하시기 바란다. 단진자가 이 정도로 까다로운 물건이었다니..;;

그럼 60도짜리 진동과 15도짜리 진동이 일치할 정도가 되려면.. 진자도 원호 궤적이 아니라 사이클로이드 궤적을 따라 움직여야 한다. 사이클로이드는 원 궤적이 아니라는 것을 이미 앞서 설명한 바 있다. 진자의 궤적이 사이클로이드가 되게 바꾸는 방법은 다음과 같이 따로 있다..!

바로 이렇게.. 반지름 a/2짜리 원을 굴려서 얻어지는 사이클로이드 모양의 벽을 반반 쪼개서 양 옆에 배치하면 된다. 그러면 아무 지점에서 진동시켜도 사이클로이드 궤적을 그리면서 완벽한 등시 등주기가 실현된다. 얘는 각도와 무관하게 진동 주기에 π*sqrt(l/g) 다음으로 원운동 진자 같은 복잡한 항이 덕지덕지 붙지 않는다. 이것을 첫 발견자의 이름을 따서 호이겐스 진자라고 부른다.

사이클로이드 궤적은 어째서 등시 강하가 보장되며, 저렇게 진자를 진동을 보정하면 어떤 원리로 사이클로이드가 되는 걸까?

우린 임의의 궤적 함수가 주어졌을 때 구슬이 끝까지 다 굴러가는 데 걸리는 시간을 구하는 함수 T를 이미 구한 바 있다. 분자는 sqrt(1+f'(x)^2) dx이고, 분모는 sqrt(2*g*f(x))이던 그 식 말이다.
그걸 써먹으면 된다. 얘를 임의의 시작점을 집어넣어서 끝까지 적분을 하더라도 항상 동일한 값이 나온다는 것을 입증하면 등시 강하 특성을 입증할 수 있다.

그런데 사이클로이드는 매개변수 형태로 표현돼 있으므로..
x = r*(θ-sinθ), y = r*(1-cosθ) 로부터
dx/dθ = r*(1-cosθ), dy/dθ = r*sinθ 를 얻는다.
그러므로 dy/dx는 양변을 r로 나눈 sinθ / (1-cosθ)가 된다.
이 점을 염두에 두면 식의 분자 부분을 다음과 같이 깔끔하게 dx 대신 dθ로 치환할 수 있다.

다음으로 분모는? f(x), 아니 y에 해당하는 r*(1-cosθ)만 대입해 주면 되는데...
우리의 문제를 풀기 위해서는 약간의 변화를 줘야 된다.
일반적인 상황이라면 최고점인 y=0일 때 속도가 0이었지만, 우리는 y>0이고 더 낮은 임의의 지점에서 가속을 시작하여 구슬을 굴리더라도 끝까지 다 구르는 데 걸리는 시간이 동일하다는 걸 입증해야 한다.

그 임의의 지점을 단순 높이로 나타내건 각도로 나타내건 그건 중요하지 않다. 하지만 우리는 원을 0도에서 180도(pi!) 반원 각도만치 굴려서 사이클로이드 궤적을 굴리는 상황을 설정할 것이므로 각도 표기를 계속 사용할 것이다.
θ0이라는 각도에서 처음으로 공을 굴렸다면 속도가 어떻게 될까?
v = sqrt(2g*(y-y0)) 로부터 sqrt( 2g*r*( cos(θ0) - cos(θ) )) 이 나온다. 각도를 빼는 게 아니라 y축 관점에서 cos 결과값을 빼 주면 된다.

무슨 말이냐 하면, 사이클로이드의 y축 매개변수 r*(1-cosθ)에서 1이 cos(θ0)로 바뀐다는 것이다.

자, 그냥 제일 높은 곳에서 처음부터 구른 것이면 θ0는 0도이기 때문에 분자와 분모에서 2a*(1-cosθ)가 통째로 약분되어 없어진다. 적분식은 θ와 무관한 상수가 되며(= 극값), 사이클로이드가 고정된 최단 강하 곡선임이 증명된다.
다음으로 분모의 1을 cos(θ0)이라는 상수로 바꾸고, 얘를 θ0부터 pi까지 정적분한 값도 θ0와 무관하게 고정된 값이 나온다는 것을 입증하면.. 이건 구르는 소요 시간이 θ0의 값과 무관한 등시 곡선임을 추가로 증명할 수 있다.

얘도 다루기가 많이 까다로워 보이지만.. 그래도 끝자락이 삼각함수에서 비교적 취급하기 쉬운 상수인 pi이며, 삼각함수들을 반각/배각 공식을 이용해 제곱으로 치환하면 제곱근 근호를 걷어내고 적분을 그럭저럭 격파할 수 있다. 이렇게 말이다.

아.. 경이롭다. =_=;; 특히 마지막에 arcsin으로 치환되는 적분 부분이 정말 압권이다.
이를 통해 θ0은 싹 사라져 버리고, θ0가 있더라도 그냥 θ0=0일 때와 동일하게 상수 시간이 도출된다는 것을 알 수 있다.

이상이다. 사이클로이드를 제대로 마스터 하려면 호이겐스 진자의 진동 궤적이 왜 사이클로이드가 되는지도 해석학적으로 유도해야겠지만.. 그건 이 자리에서는 생략하겠다.
아무쪼록 (1) 사이클로이드가 원이나 타원의 호가 아닌 이유, (2) 저게 최단 강하 곡선인 이유, (3) 어느 위치에서건 등시 강하 곡선인 이유를 제대로 설명할 수 있다면 당신은 대학 나온 훌륭한 이과생 공돌이라고 불릴 자격이 될 것이다.

1600년대 중후반은 갈릴레오와 케플러에 이어 뉴턴, 라이프니츠, 베르누이 같은 사람이 등장하면서 미적분학이 태동하고 고전역학이 전성기를 맞이한 시기였다. 그 옛날 사람들이 사이클로이드라든가 단진자 운동의 특성을 갖고 저런 고민을 하고 있었던 것이다.

특히 저 때는 괘종시계가 현역이던 옛날이었기 때문에 단진자 운동을 정확하게 기술하고 등주기를 실현하는 것이 매우 중요했다. 그게 시계의 정확도와 직결됐기 때문이다.
그러다 1700년대에 가서는 오일러와 라그랑주가 나오면서 이 바닥은 더 세련된 계산법이 개발되고 발전을 이루게 되었다.;;

Posted by 사무엘

이전 글들에서는 현수선 얘기를 하면서 한창 쌍곡선함수 얘기를 늘어놨는데, 이 글에서는 분위기를 바꿔 정통(?) 삼각함수 얘기를 좀 하겠다.
수학에서 다루는 많고 많은 곡선 중에는 “원을 직선 위에서 굴릴 때 그 원에 놓인 정점이 그리는 궤적”이란 게 있다. 이걸 ‘사이클로이드’라고 한다.

반지름 r인 원이 (0, r) 위치에 놓여 있다. 그리고 궤적을 추적하고자 하는 점은 처음에 바닥의 원점 (0, 0)에 있다고 치자.
수학 좌표계는 x의 양의 방향이 오른쪽이고 y의 양의 방향은 위쪽이다. 이 상태로 원이 x의 양의 방향으로 굴러가려면 시계 방향으로 굴러가야 하며, 각도는 처음에 270도에서 시작했다가 줄어들어야 한다. 각도가 늘어나는 방향은 반시계 방향이기 때문이다.

즉, (cos(3π/2 - θ), sin(3π/2 - θ)+1) 정도 될 텐데..
cos(3π/2 - θ)는 sin(-θ) → -sin(θ)로 간소화시킬 수 있다.
sin(3π/2 - θ)도 -cos(θ)로 간소화시킬 수 있다.

이건 원이 제자리에서만 빙글빙글 도는 상황이다.
실제로 굴러간다는 조건을 추가하면 원은 아주 단순하게 x축의 양의 방향으로 r*θ만치만 이동하게 된다. 원의 전체 둘레는 2πr이고 θ는 각도 겸 원호의 둘레와 정확하게 대응하기 때문이다.

그러므로 사이클로이드의 궤적은 ( r*(θ-sinθ), r*(1-cosθ))라고 깔끔하게 나온다. 원이 헛돌지 않고 제대로 굴러가는 이상, 점이 아예 뒤로 후퇴하는 일은 어떤 경우에도 절대 없다는 걸 알 수 있다.

사이클로이드는 원이나 타원의 호와 비슷하게 생겼지만, 실제로는 이와 무관한 별개의 궤적이다. 아래의 그림 비교와 관련 설명을 참고하시라.

그리고 얘는 x와 y의 위치를 매개변수를 통해 제각기 나타낼 때는 식이 저렇게 아주 깔끔하게 구해지는 반면, y=f(x) 꼴의 단순한 양함수로 나타내는 건 굉장히 복잡하고 까다롭다. x축이 그냥 sin(t)가 아니라 t-sin(t)인데.. 이게 역함수를 구하기가 몹시 난감하기 때문이다.

그나마 x=g(y)라는 일종의 음함수에 가까운 형태로 나타내는 게 y=f(x)보다는 더 할 만하다. 원이 굴러간 거리에 대한 함수가 아니라 원의 범위 영역에 대한 함수 말이다.
사이클로이드는 이렇게 까다로운 면모가 있음에도 불구하고 한 사이클 궤적의 길이라든가 그 궤적 아래의 면적은 적분을 통해 깔끔하게 떨어지는 형태로 구할 수 있다. 이쪽으로 더 관심 있으신 분은 위키백과 등의 타 사이트를 참고하시라.

이 글에서 현수선 다음으로 사이클로이드를 소개한 이유는 얘도 현수선과 동급으로 역학적으로 아주 흥미로운 특성이 있는 물건이기 때문이다.

1. 최단 강하

먼저, 얘는 일명 ‘최단(최고속) 강하 곡선’이다. 높은 지점에서 낮은 지점으로 공을 굴리는데 무작정 최단 거리인 직선 경사로가 아니라, 사이클로이드를 상하 반전시킨 형태의 경사로를 만드는 게 좋다. 그러면 공이 중력 버프를 받아서 목적지에 더 빨리 도달하게 된다! (지면 마찰과 공기 저항 따위는 모두 무시)

그렇다면 비행기의 비상 탈출용 미끄럼틀도 직선이 아니라 이런 형태로 만드는 게 더 나을 것 같다. 물론 현실적으로는 무리이겠지만, 그래도 어린이용 미끄럼틀 중에는 이런 과학 고증(?)을 반영하여 사이클로이드 곡선을 흉내 낸 모양인 것도 있다.

그런데 의문이 든다. 이것도 까놓고 말해 그냥 포물선이라든가, 사분원이나 2차 베지어 곡선, 혹은 아예 역학적인 안정성이 검증돼 있는 현수선이 최단 강하일 수도 있을 텐데 왜 하필 사이클로이드가 당첨인 걸까? 직선보다 아래로 볼록한 모양이어야 하겠다는 건 수긍이 가지만 왜 하필 저 모양이 최적인지는 직관적으로 납득이 잘 안 된다.

먼저 우리는 구슬이 처음 놓여 있는 좌측 최상단 꼭대기가 원점 (0, 0)이라고 가정하자. 그리고 계산의 편의를 위해, y축은 중력이 향하는 방향(=아래)이 +로 증가하는 방향이라고 간주하도록 하겠다. 즉, 통상적인 수학 좌표가 아니라 컴퓨터 화면의 좌표계를 사용한다는 것이다.
그러면 구슬은 아래로 굴러가면서 x축과 y축 모두 값이 일관되게 증가한다고 생각할 수 있으며, 저 사이클로이드 공식도 y축의 부호를 뒤집을 필요 없이 그대로 사용할 수 있다.

이 문제를 푸는데 매우 중요하게 활용되는 단서는 (1) "역학적 에너지 보존의 법칙"이다. 구슬이 직선 경사로를 쫙 구르건 그 어떤 꼬불꼬불한 곡선을 타고 오르내렸건, y축 중력 가속도가 g인 상태에서 y라는 높이만치 내려가 있다면 그 당시에 물체의 속도는 mgy = mv^2 /2를 근거로 v=sqrt(2*g*y)가 된다. 위치 에너지가 그만치 운동 에너지로 바뀌었음을 뜻한다. 당연한 말이지만 x축과는 전혀 무관하다.

이 속도는 xyz 같은 축을 총체적으로 고려한 단위 시간당 이동량이다. 그 속도를 얻은 상태에서 수평 이동을 한다면 구슬은 공기 저항과 마찰이 없는 한, 영원히 등속 운동을 할 것이다. 상승하면 속도가 점차 느려질 것이고, 하강하면 속도가 붙어서 빨라질 것이다.

여기까지 준비가 완료됐으면 사이클로이드 문제는 크게 두 방법으로 풀 수 있다.
하나는 뉴턴이 터를 닦으시고 오일러-라그랑주가 끝장을 낸 (2) 변분법을 동원하는 것이다. 하드코어한 고전역학의 범주에서 끝을 보는 것이다.
다른 하나는 파동 분야에서 정립된 (3) 스넬의 법칙을 접목하는 것이다. 겉보기로 수식의 압박이 변분법보다는 '약간' 덜할지 모르지만, 그럼 스넬의 법칙은 왜 어째서 성립하는지를 일일이 따지고 든다면 난이도는 비슷하게 안드로메다로 치솟는다.

그럼 변분법 버전부터 먼저 살펴보도록 하겠다.
통상적인 미분이 함수의 극점을 구해서(= 도함수가 0) 특정 구간에서 함수의 최소/최대값을 구하는 데 쓰인다면, 변분법이란 범함수의 최소/최대값을 구하는 방법론을 말한다.
그럼 범함수란 무엇이냐? 프로그래밍에는 평범한 숫자나 객체가 아니라 함수 자체나 람다를 다른 함수의 인자로 넘겨주는 게 있다. 그것처럼 수학에도 함수를 받아들여서 스칼라 형태의 값을 되돌리는 함수가 있는데, 그걸 범함수(functional)라고 한다. 특정 함수가 특정 구간에서 미분 불가능한 지점의 개수.. 그런 것도 범함수의 일종이 될 수 있다.

변분법을 이용하면 두 점을 잇는 가장 짧은 경로가 직선인 이유처럼 공리 수준의 너무 당연해 보이는 것부터 시작해서..
둘레가 동일한 도형 중에 면적이 최대인 놈이 원의 형태가 되는 이유, 물방울· 비누 방울이나 잠수정이 전부 구형으로 만들어지는 이유(단위 면적당 압력 최소화) 같은 것도 다 수학적으로 엄밀하게 유도할 수 있다.

최단 강하 곡선 문제에서 우리가 구해야 하는 것은 길이나 면적 따위가 아니라 "도달 시간"의 최소값이다.
구슬이 위에서 아래로 굴러가는 궤적을 y = f(x)라는 함수로 나타낸다면, a라는 임의의 x축 지점에서 구슬의 진행 속도는 f(a)의 값으로부터 구할 수 있다. 속도는 앞서 공식을 구한 바와 같이 전적으로 y축에 의해서만 결정되고, y축의 값은 x축 대한 함수 f로부터 구할 수 있으니 말이다.

그렇다면 (2-1) 이 함수를 어째 잘 적분해서 f(x)라는 함수에 대해 구슬이 다 내려갈 때까지 걸리는 시간도 구할 수 있을 것이다.

이건 흔히 떠올릴 수 있는 상황은 아니다. 속도 함수를 적분해서 구하는 건 보통은 거리이기 때문이다. 시간에 대해 적분하면 끝이다. (예: 시속 100km로 2시간을 달린 거리는 200km)
그런데 반대로 소요 시간을 구하기 위해서는 반대로 함수 궤적의 거리가 주어져 있어야 한다. (예: 시속 100km로 300km를 달리는 데 걸리는 시간은 3시간) 그래도 이것도 적분이긴 하다.

앞서 sqrt(2*g*y)이라고 값을 구한 속도 v는 거리/시간, 즉 ds/dt라는 개념이다. 그런데 이 ds라는 건 역시 x 변화량 대비 y의 변화량을 거리화한 것이며, y 변화량은 곧 f(x)의 변화량과 같다. 그러므로 이것은 sqrt(1 + f'(x)^2 )로 나타낼 수 있다.
v = ds/dt 에서 sqrt(2*g*f(x)) = sqrt(1 + f'(x)^2 ) / dt 가 되고..
이 관계로부터 dt = sqrt(1 + f'(x)^2 ) / sqrt(2*g*f(x))이 된다.

오.. 그러므로 구슬이 구르는 궤적 함수가 f이고 중력 가속도는 g, 구슬이 다 구른 오른쪽 끝의 x축 지점이 a라 할 때, 구슬이 다 구르는 데 걸리는 시간 T는 다음과 같이 깔끔하게 구해진다.

여기까지 도달했으면 문제가 반 정도는 해결됐다고 볼 수 있다. 우리는 a와 g가 고정돼 있을 때 T를 최소화하는 f(x)를 구하면 된다.

1/sqrt(2*g)는 그냥 상수이므로 적분 기호 밖으로 옮겨도 아무 상관 없다. 그리고 범함수에서는 그 정의상 x라는 변수뿐만 아니라 그 x에 대한 함수 f(x)까지 범함수의 parameter가 될 수 있다. 그렇기 때문에 f(x) 대신 그냥 y로 표기하며, 도함수도 f'(x) 대신 dy/dx라고 표기하는 걸 더 일상적으로 보게 된다. 애초에 사이클로이드도 f(x) 대신 x, y축 따로 매개변수 형태로 표기하는 게 더 유리하기도 하고 말이다.

이 문제를 풀기 위해 쓰이는 도구는 바로 (2-2) 오일러-라그랑주 방정식이다.
x, y라는 변수가 있고 F가 y, y', x에 대한 범함수라고 하자. 우리가 푸는 문제에서는 x, y는 구슬의 궤적을 나타내며, F는 그 궤적으로 끝까지 구르는 데 걸리는 소요 시간을 구하는 구간 적분이 된다.
오일러-라그랑주 방정식에 대해 제일 간단하고 엉성하게 요점만 말하자면, F가 극값(최소 또는 최대)이 나올 때 이들은 다음 등식을 만족한다.

(왜 그런지 궁금하면 이변수함수의 연쇄법칙을 동원해서 저 식을 직접 유도하면 된다. 하지만 이 자리에서는 시간과 지면의 부족으로 증명을 생략하겠다. ㄲㄲ)

저 식에서 F에다가는.. 우리가 구한 처음 식 T에서 상수배 항과 dy 적분을 걷어낸 sqrt((1+x'^2)/y), 즉 순간 변화량을 대입한 뒤, 식을 x'에 대해 풀면 된다.
중요한 것은 우리의 경우, ∂F/∂x가 0이 보장된다는 것이다. 앞서 살펴보았듯이, 물체의 속도는 x축 위치와는 전혀 무관하고 y축 높이에 의해서만 결정되기 때문이다.

그러니 저 식에서 d/dy (∂F/∂x')도 같이 0이어야만 한다. F를 x'에 대해 편미분한 뒤, 양변에 sqrt(y)를 곱한 결과는 아래와 같이 된다. (x가 어떤 함수인지 정확한 정체를 모르기 때문에 x와 x'는 서로 독립변수로 간주됨) 이 식을 x'에 대해서 정리하면..

헥헥.. 이제 x'이 구해졌다. 그러면 함수 x는 y에 대해 적분을 해서 구할 수 있긴 하지만.. sqrt(x/(1-x))라는 함수는 부정적분을 호락호락 쉽게 구할 수 있는 놈이 아니다.
쟤를 수월하게 적분하는 방법은 x, y를 다른 변수 형태로 치환하는 것이다. 애초에 사이클로이드는 x, y 궤적을 매개변수 형태로 치환해야 표현하거나 취급하기 용이한 물건이다.

y를 sin(t)^2 / C^2 으로 치환하면 거추장스러운 C가 없어진다. 그리고 근호 안의 식이 sin(t)^2 / cos(t)^2로 바뀌고 근호도 없어져서 식 전체가 tan(t)로 바뀌는 마법이 펼쳐진다.
단, dy도 sin(t)^2의 도함수인 sin(t)*cos(t) dt로 바뀌기 때문에 저 tan(t)에다가 sin(t)와 cos(t)를 곱해 줘야 한다.
tan은 sin/cos이므로 cos는 서로 약분되어 없어지고.. 최종적으로 적분해야 하는 식은 sin(t)^2 dt가 된다.

그리고 sin(x)^2은 삼각함수 덧셈 정리로부터 유도된 반각 공식에 의거하여 (1-cos(2x))/2로 처분 가능하다. 이게 적분하기 훨씬 더 편하다.
사이클로이드를 기술하는데 각도가 t건 2t건 그건 중요하지 않으므로 x축의 궤적은 각도 θ에 대해 C*(θ-sin(θ))가 도출되며, y축은 이미 sin(t)^2의 간소화형인 C*(1-cos(θ))로 답이 나와 있다. 이것으로 유도 끝..

우리는 사이클로이드의 x, y축별 매개변수식에서 아주 중요한 특성을 하나 주목하게 된다. 바로 매개변수 t에 대해서 x축의 궤적 함수는 y축 궤적 함수의 부정적분이라는 것이다! 반대로 y축의 궤적 함수는 x축 궤적 함수의 도함수이다. 애초에 이런 관계였구나..

이것은 사이클로이드를 매개변수가 아닌 양/음함수로만 기술할 때는 간파할 수 없는 특성이다. 그리고 이런 특성이 존재하기 때문에 사이클로이드의 x, y 궤적은 앞서 제시되었던 미분 방정식을 만족하고 해당 범함수에 대해 오일러 방정식을 충족하고, 최단 강하 곡선 역할까지 한다고 볼 수 있다.

이상이다. 현수선하고 뭔가 비슷한 구석이 있는 것 같으면서도 현수선을 분석하는 것보다는 확실히 더 어려운 것 같다..;; 현수선이 역학적으로 자연스럽고 안정된 궤적이라면, 사이클로이드는 좀 더 인위적이고 최적화된 듯한 느낌이 드는 궤적이다. 다만, 둘 다 중력이 있기 때문에 존재한다는 공통점이 있다.

얘는 중력이 작용하는 지표면에서 공을 몇 도로 던졌을 때 제일 멀리 날아가냐 하는 문제와도 비슷한 느낌이 든다. 삼각함수의 반각 공식이 쓰였다는 공통점도 있으니 말이다. 하지만 사이클로이드는 그것보다도 당연히 훨씬 더 복잡하고 난해하다.
글이 이것만으로도 너무 길어졌으니, 최단 강하 증명의 다른 풀이법 등 나머지 얘기는 다음 시간에 계속하도록 하겠다. =_=;;

Posted by 사무엘