원소가 0 아니면 1 두 종류밖에 없는 N*N 크기의 어느 정사각행렬 M(N)이 있다. N은 2의 거듭제곱 형태로만 가능하며, M(N)의 생성 규칙은 이러하다.
일단, 크기가 1인 M(1)은 그냥 {0} 하나뿐이다.
그 뒤, M(2*n)은 M(n)의 각 원소들에서 0과 1을 뒤바꾼 놈을 M(n)의 왼쪽과 위쪽, 그리고 좌측 상단에 총 3개 카피를 씌우는 형태로 생성된다. 그러므로 M(2)는
(1 1)
(1 0)
이 되며, 다음 M(4)는 쟤를 뒤바꾼 놈을 또 덧붙여서
(0 0 0 0)
(0 1 0 1)
(0 0 1 1)
(0 1 1 0)
이 된다. 생성 규칙이 이런 식이다.
이런 식으로 M(16), 더 나아가 M(256)을 그림으로 나타내면 이런 모양이 된다.

흐음. 무슨 프랙탈 같기도 하고..
이런 행렬은 고안자의 이름을 따서 Walsh 행렬이라고 부른다.
그런데, 모노크롬이나 16색을 어렵지 않게 접할 수 있던 옛날에 이런 무늬를 화면에다 깔아 놓으면 꽤 근사해 보였을 것 같다~!
이걸 갖고 더 재미있는 장난을 칠 수도 있다.
옛날옛적에 학교에서 전자· 컴공을 전공했던 분이라면 혹시 그레이 코드(gray code)라고 기억하는 분 계신가?
통상적인 2진법과 달리, 숫자가 1씩 증가할 때 언제나 1개의 비트만이 바뀌게 숫자를 특이하게 표현하는 방식이다. 즉, 01111이다가 10000으로 바뀌는 식의 격변이 없다는 것이다. 물론 이런 숫자 인코딩을 갖고 진지한 산술 연산을 할 수는 없지만, 다른 용도로 쓸모는 있다고 한다.
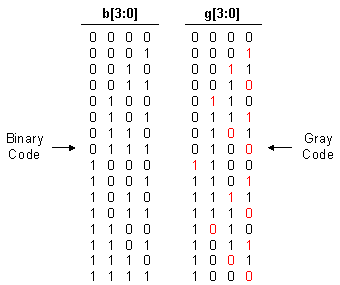
0 1 3 2 6 7 5 4 ...
난 저걸 봐도 비트를 flip하는 규칙 자체를 잘 모르겠다. 숫자가 커질수록 긴가민가 헷갈린다. 솔까말 이거 규칙을 찾는 걸로 IQ 테스트 문제를 내도 될 것 같다.
그런데 일반 숫자를 그에 상응하는 그레이 코드로 바꾸는 공식은 어이없을 정도로 간단하다. x^(x>>1), 다시 말해 자신의 절반값과 자신을 xor 하면 된다.
자, 여기서 끝이 아니다.
저 수열에서 각 숫자들을 구성하는 2진법 비트의 배열 순서를 뒤집어 보자. 10진법으로 치면 1024를 4201로 바꾸는 것과 같다.
비트를 shift나 rotate하는 게 아니라 reverse 하는 건 내가 알기로 왕도가 없다. 그냥 for문 돌려서 1비트씩 차근차근 처리하는 수밖에 없다. 마치 주어진 숫자를 2진법으로 표현했을 때 1의 개수를 구하는 것처럼 말이다.
비트 수가 고정돼 있고 속도가 무진장 빨라야 한다면 미리 계산된 테이블을 참조해야 할 것이다.
N=8이라면 비트 자릿수는 3일 테고.. 0 1 3 2는 2진법으로 각각 000, 001, 011, 010일 텐데,
이걸 뒤집으면 차례대로 000, 100, 110, 010.. 즉 0 4 6 2 ... 형태로 바뀐다. 이 정도면 완전 난수표 수준으로 숫자를 뒤섞은 거나 마찬가지로 보인다.
저 수열이 확보됐으면 그걸 토대로 기존 Walsh 행렬을 개조해 보자. 즉, 지금 줄 배열이 0 1 2 3 4..의 순인데, 그걸 0 4 6 2 ... 즉, 둘째 행(1)에다가 다섯째 행(4)을 집어넣고, 다음 행에다가 일곱째 행(6)을 넣는 식으로 순서를 바꾼다. 그러면..

이런 인상적인 모양의 무늬가 만들어진다. 이것도 크기별로 규칙성이 있다. 좌측 상단은 사각형이 큼직하고, 우측 하단으로 갈수록 픽셀이 조밀해진다.
얘는 여러 명칭으로 불리는데, 통상적으로는 Walsh 행렬의 Hadamard 변환이라고 불린다.
실제 저 행렬/테이블을 구하는 건 아무 프로그래밍 언어로나 10분이면 코딩 가능할 것이다. 참고로 비트 reverse 같은 난감한 동작 없이 저 행렬을 얻는 다른 계산법도 존재한다.
이런 무늬 행렬은 전자공학 신호 처리 쪽에서 쓰인다고는 하는데.. 난 그쪽을 전공하지 않아서 잘 모르겠다. 단지 0과 1만 갖고도 인간 두뇌의 잉여력이 얼마나 폭발할 수 있는지에 경이로움을 느낄 따름이다.
수 년 전에 디더링 패턴의 생성 규칙에 대해 글을 쓰고 나서 이런 재귀적인 무늬를 주제를 다룬 건 무척 오랜만이다. xor은 온갖 난수와 암호도 만들어 내는 이산수학과 정보 이론의 진수임이 틀림없어 보인다. 세상에 이런 게 있다는 걸 알게 됐다는 차원에서 간단히 글을 남기게 됐다.
(xor은 x-y 2차원 평면에다가 진리표를 나타냈을 때 0과 1 결과를 직선 하나로 단순 분류할 수 없는 유일한 연산이기도 하다. 일명 XOR 문제..;; 마치 특정 그래프에 대해 한붓그리기가 불가능한 것과 비슷한 인상을 주는데.. 과거에 한때는 퍼셉트론 무용론과 함께 AI 겨울을 야기한 이력이 있다.)
Posted by 사무엘


