자동차가 나아가면서 그리는 궤적은 직선 아니면 원호이다. 핸들을 꺾은 채로 가만히 있으면 좌우 어디로든 원호 궤적을 그린다.
그렇기 때문에 도로의 커브 역시 이런 모양을 염두에 두고 설계된다. 고속도로는 커브의 회전 반경이 더 크다. 하지만 직선과 원호만이 궤적의 전부가 아니며, 그 중간 단계에 속하는 궤적도 쓰인다.
그것은 바로 클로소이드(clothoid curve)이다. 얘는 정속 주행하면서 핸들을 일정한 각속도로 돌릴 때 차량이 그리는 궤적이다.
핸들이 돌려져 있긴 하지만 그 각의 변화가 없는 채로 차가 정속 주행하면 잘 알다시피 원호가 그려진다. 그러나 그 곡률도 일정하게 변하면 저런 더 복잡한 곡선이 나온다는 것이다. 간단히 코딩을 해서 궤적을 그려 볼 수도 있다.
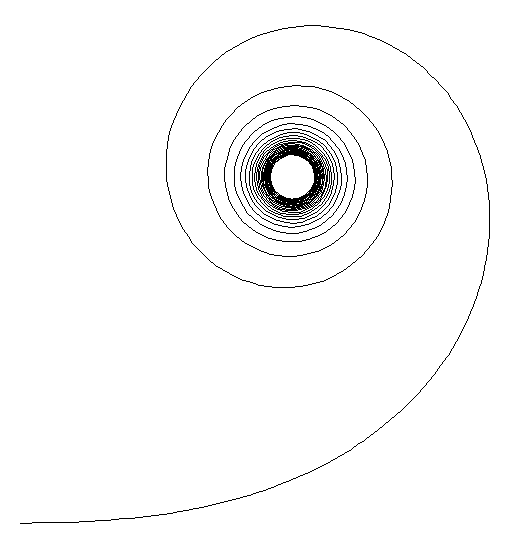
차를 몰고 이런 커브를 돈다고 생각해 보자. 핸들을 서서히 더 꺾어야겠다는 생각이 절로 들 것이다.
이 궤적은 보다시피 각에 정비례해서 중심으로부터의 거리를 일정하게 줄였을 때 나오는 소용돌이 궤적과는 다르다. 매개변수를 통해 수학적으로는 이렇게 표현된다고 한다.
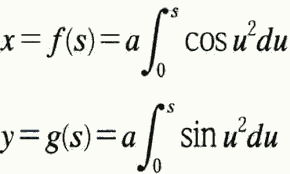
원호라면 [cos(t), sin(t)]라고 너무 간단하게 표현되겠지만, 움직이는 동안 각도가 계속 변하다 보니 식이 저렇게 이상하게 바뀌었다.
극좌표로는 어째 표현할 방법이 없는가 모르겠다. 원호는 아예 상수가 되어 버리는데 말이다. 다만, 얘는 직교좌표에 친화적인 직선과도 접점이 있는 물건이기 때문에 극좌표를 동원한다고 해도 더 간편· 간단한 형태가 나오지는 않을 것 같다.
cos(x)^2가 아니라 cos(x^2)라는 걸 유의하시라. 이건 고등학교 수준의 삼각함수 덧셈 정리의 제곱 법칙 등으로도 전혀 요리할 수 없다. 저 함수의 부정적분은 같은 초등함수들의 조합으로 나타낼 수 없다.
이 궤적은 그래도 중심점에 완전히 붙어 버리지는 않고 뱅글뱅글 돌게 된다는 게 특징이다. 그래도 현실의 자동차는 핸들을 무한히 꺾을 수 없기 때문에 도로에서는 이 궤적의 극히 일부만을 이용해서 직선과 원호를 연결하게 된다. 이런 식으로 말이다.
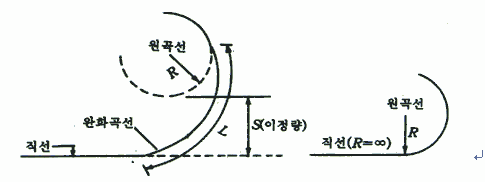
직선과 원호만 적절히 연결해도 수학적으로는 연속이고 미분 가능한 궤적이 나온다. 하지만 그걸로 충분치 않아서 운전자가 핸들을 돌리는 속도까지 감안한 완화 곡선이 쓰인다는 게 신기하지 않은가?
이 개념은 심지어 핸들이라는 게 존재하지 않는 철도에서도 예외 없이 쓰인다. 그래서 R=400, R=3000짜리 커브라고 해도 그 지도에다가 반지름이 그만 한 원을 그려 봐도 철길의 선형은 그 원보다 훨씬 더 완만해 보인다.
이게 천체의 운동이나 우주 탐사선의 궤적을 기술하는 식과 접점이 있으려나..?? 당장 사고실험을 해 봐도 그건 운동하는 방식이 완전히 다른데 같을 리가 없어 보인다. 하지만 심상이 서로 미묘하게 비슷해 보인다.
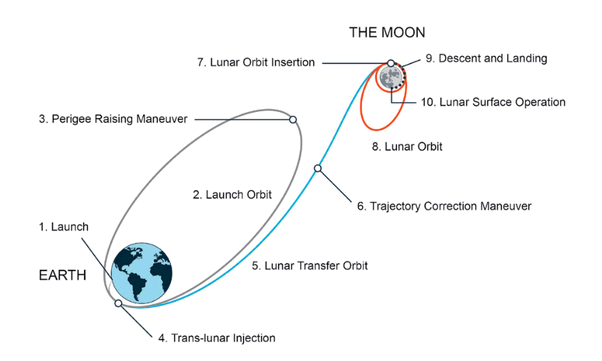
이렇듯, 몇백 년 전에 유럽의 수학자들은 자연과 일상생활에서 발생하는 어지간한 운동들을 몽땅 다 미적분 해석학으로 기술해 냈다. 예전에 다뤘던 사이클로이드, 현수선 같은 것 말이다. 그것도 컴퓨터나 계산기가 없던 시절에 머리와 종이만으로 증명을 해 내다니.. 생각하면 생각할수록 경이롭다.
Posted by 사무엘


