* 꽤 오래 전인 블로그 개설 초창기에 썼던 글을 리메이크 한 것이다.
옛날에 컴퓨터 학원에서 GWBASIC을 중급이나 고급까지 공부해 본 분이라면, 마지막 단원인 그래픽을 공부하면서 이런 비슷한 그림을 하나 그려 본 추억 정도는 있을 것이다.
그리는 방법은 간단하다. 세로줄을 하나 그은 뒤, 그 선의 윗점은 아래로 n만치 낮추고 아랫점은 오른쪽으로 동일한 n만치 옮겨서 선을 긋기를 반복하면 된다. 세로줄이 완전히 가로줄로 바뀔 때까지.
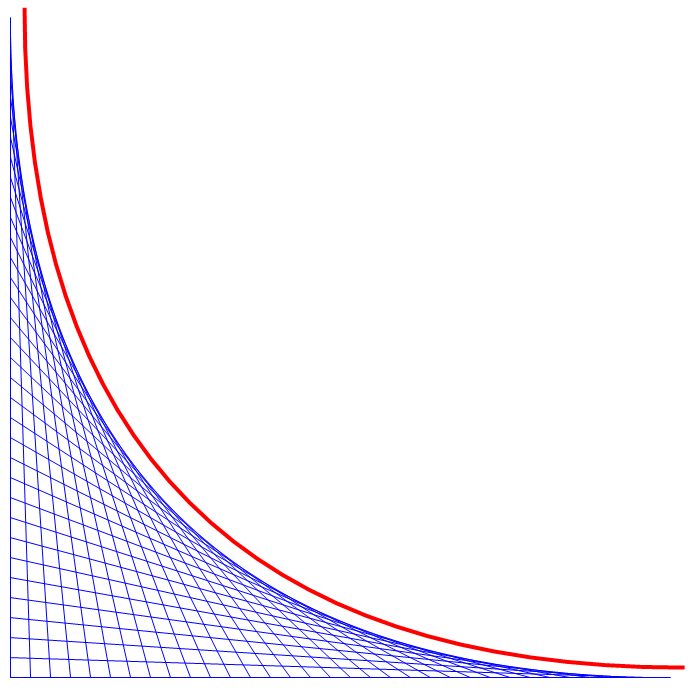
그 단순함에 비해서 생긴 결과물은 꽤 '컴퓨터그래픽스럽고' 뭔가 멋지다는 느낌이 들지 않는지?
그런데 여기서 의문이 생긴다.
저런 식으로 선을 한없이 많이 그어 나갈 때, 가장자리에 형성되는 저 둥그런 곡선은 수학적으로 어떤 의미를 갖는 곡선으로 수렴하게 될까? (그림에서 붉은 곡선) 편의상 선을 (0,0)-(0,1)에서 (0,0)-(1,0)까지 긋는 상황을 가정한다면 어떤 곡선이 그려질까? 이거 굉장히 재미있는 문제이다.
x축 (a, 0)와 y축 (0, b)를 지나는 직선의 그래프는 y = -(b/a)*x + b 이며 이건 중학교 수준으로도 알 수 있는 사실이다.
이 그림에서는 0~1 사이의 a에 대해서 (a, 0)과 (0, 1-a) 사이를 지나는 직선이 만들어지므로 방정식은 y = -((1-a)/a)*x + (1-a)가 된다. 이 식을 [1]이라고 설정하자.
그러면 이 a 지점에서 그어진 직선은 우리가 구하고자 하는 미지의 곡선에서는 어느 지점과 만나게 될까? 이걸 생각하는 게 문제를 푸는 열쇠이다.
a 지점에서 그어진 직선이 곡선의 표면에 닿는 지점은 바로.. 그 직선의 바로 극소량 떨어진 옆에 있는 또 다른 직선과의 교점일 것이다. 극한이라는 개념이 필요해진다.
a 지점에서 x축과 y축이 b만치 극미량 전진하여 (a+b, 0)과 (0, 1-a-b)를 지나는 직선의 방정식은 y = -((1-a-b)/(a+b))*x + (1-a-b) 가 된다. 이 식을 [2]라고 한다.
두 직선 [1]과 [2]의 교점을 구하려면 두 식을 연립해서 x, y에 대해서 방정식을 풀면 된다.
그럼 x=a*(a+b), y=(a-1)*(a-1+b)가 나온다.
b가 0에 한없이 가까워져서 두 직선이 근접하게 되면 교점은 결국 (a^2, (a-1)^2)라고 a에 대한 매개변수식으로 귀착된다. 곡선의 궤적이 이렇게 다 구해진 것이다. 게다가 문제 접근 방식의 특성상, x=a^2인 지점에서 곡선의 기울기도 -((1-a)/a)라고 딱 구해졌다.
x의 매개변수식이 a^2이니 (a-1)^2에다가 루트만 씌우면 끝나고, 그리고 기울기의 부정적분을 구해서 f(0)일 때 1이 나오는 상수 C를 덧붙여 줘도 게임 끝이다.
곡선의 방정식은 x-2*sqrt(x)+1, 또는 y = (1 - sqrt(x))^2 이 된다. 오옷~~~ 비슷한 4사분원의 방정식과 비교했을 때 근호와 제곱의 위치만 싹 맞바뀐 형태라는 게 흥미롭다.
이 정도 문제는 난이도가 고등학교 교과 수준이거나 좀 아슬아슬하게 넘는 수준일 것 같다.
임의의 지점에서 기울기가 저렇게 결정되는 곡선을 구한다는 특성상, 제일 확실하게 푸는 방법은 미분 방정식을 동원하는 것이겠지만.. 그 정도면 확실하게 고등학교 수준은 아니다.
곡선의 식이 정확하게 나왔으니 곡선의 성질도 다 알 수 있다. 저 선들이 차지하는 면적은 1/6이 된다(0부터 1까지 식을 적분한 값). 곡선과 y = x와의 교점, 다시 말해 곡선의 기울기가 정확하게 -1이 되는 지점이며 곡선 내부에 존재할 수 있는 가장 큰 정사각형의 한 변 길이는 1/4임을 알 수 있다.
그리고 또 하나 짚고 넘어갈 점이 있다.
위의 그림에서 빨간 곡선은 내가 손으로 그었을 리는 없고.. 어떻게 그린 걸까?
(a^2, (a-1)^2)라는 궤적은 베지어 곡선의 한 형태이다. 근사가 아니라 2차 베지어 곡선과 수학적으로 완벽하게 일치한다.
시작점 P0, 제어점 P1, 끝점 P2로 이뤄진 2차 베지어 곡선의 식은 (1-t)^2*P0 + 2*t*(1-t)*P1 + t^2*P2 (0<=t<=1)이다.
참고로 임의의 n차 곡선의 식은 각 항의 계수가 1, 3, 3, 1 등 이항정리 계수의 형태로 변하면서 t의 거듭제곱은 증가하고, (1-t)의 거듭제곱은 감소하는 형태로 생성된다.
저 식을 점들의 좌표가 아니라 t에 대해서 풀면 (P0 - 2*P1 +P2)*t^2 + (2*P1 - 2*P0)*t + P0 이 남는다.
문제의 곡선의 매개변수 식을 보면 x축은 a^2로, 2차항 t^2의 계수만 1이고 나머지는 0이다[1, 0, 0]. 따라서 P0은 답정너 0이 되어야 함. 일차항도 P0이 0으로 소거되고 없으면서 전체 계수가 0이 돼야 하므로 P1 역시 0이 된다.
한편, 이차항은 P0과 P1이 모두 0인 상태에서 계수가 1이 돼야 하므로 혼자 남은 P2는 0이 된다. P0, P1, P2의 x축 좌표는 각각 (0, 0, 1)로 정해졌다.
y축으로 가 보면, (a-1)^2는 a^2 - 2*a + 1이므로 맞춰야 하는 계수는 [1, -2, 1]이 됐다. 이로써 상수항 P0은 1부터 시작한다. 그 다음으로 2*P1 - 2*P0이 -2가 되어야 하는데 P0이 이미 1이라면.. P1은 0이 돼야 0-2 = -2가 될 수 있다.
P0도 값이 자동으로 정해진다. P0 - 2*P1 + P2 = 1이어야 하고, P0이 1이므로 P1뿐만 아니라 P2도 0으로 결정된다. P0, P1, P2의 y축 좌표는 각각 (1, 0, 0)이 된다.
이게 무슨 뜻인가? (a^2, (a-1)^2) 매개변수 곡선은 시작점 (0, 1), 제어점 (0, 0), 끝점 (1,0)인 아주 기초적인 2차 베지어 곡선과 동일하다는 얘기이다. 아니 그러고 보니, 베지어 곡선을 수식이 아니라 직관적으로 그리는 방법 중에도 한 선분을 저 그림과 비슷한 방식으로 다른 선분으로 점진적으로 변화시켜서 그 궤적을 연결하는 게 있었다. 심오함이 끝이 없구나..!
보통 그래픽 프로그램에서는 제어점을 2개를 둬서 2차보다는 더 범용적인 3차 베지어 곡선을 지원하는데, 3차 베지어 곡선의 표현력은 당연히 2차 곡선의 그것의 상위 호환이다.
3차 베지어 곡선의 방정식을 역시나 t 변수에 대해서 나타낸 뒤 2차 베지어 전개식과 계수가 일치하도록 방정식을 풀어 보면.. 시작점 P0과 P2는 동일하고 중간점이 P1일 때,
C1 = (2*P1+P0)/3 , C2 = (2*P1+P2)/3
이라는 식이 나온다. 이렇게 두 중간점을 잡아 주면, 3차 베지어 곡선으로 2차 베지어 곡선을 정확하게 나타낼 수 있다.
베지어 곡선으로 수학적으로 100% 완벽하게 표현할 수 없는 유명 요소가 두 가지가 있는데.. 하나는 원/원호이고 다른 하나는 다른 베지어 곡선과 굵기만 다르면서 평행한 파생 곡선이다. 쉽게 말해서 철도 선로의 한 곡선 궤조에 대응하는 다른쪽 궤조 말이다.
그에 반해 저렇게 직선을 찍찍 그어서 자연스럽게 만들어진 곡선 궤적은 매개변수로 표현하나 일변수 형태로 표현하나 식이 딱 구해지고 초월함수 그딴 거도 안 나오고 부정적분도 구해지고.. 마음대로 요리가 되는 게 좋다.
사이클로이드(최단 강하 궤적)라든가 현수선 같은 곡선 문제도 수학 해석적 관점에서 아주 재미있는 주제인데 이것도 나중에 다룰 기회가 있으면 좋겠다.
이 글은 5년 전에 썼던 오리지널에 비해 베지어 곡선 얘기도 들어가고 그림도 GDI가 아닌 GDI+의 앤티앨리어싱이 들어간 것으로 바꾸는 등 내용의 품질을 대폭 향상시켰다. ^^
Posted by 사무엘


