수학에서 다루는 수 중에는 음수라는 게 있다. 얼마를 빼는 것은 음수를 더하는 것과 동급으로 치자고 발상의 전환을 한 것이다. 그래서 0의 양 옆으로 양수와 음수가 존재하게 됐다.
음수는 덧셈· 뺄셈· 곱셈· 나눗셈이라는 기본 사칙연산 범주에서는 별로 어려울 게 없다. 곱셈과 나눗셈에서는 부호가 마치 xor 연산과 비슷하게 바뀐다는 것만 염두에 두면 된다. (둘 다 동일하면 양수, 다르면 음수) 뭐, 음수라는 개념뿐만 아니라 -1 곱하기 -1이 어째서 +1이 되는지도 마냥 직관적으로 쉽게 이해 가능한 개념은 아닐 수 있는데..
더 나아가 실수 나눗셈 말고 '나머지'를 같이 구하는 정수 나눗셈에서는 피연산자에 음수가 섞여 있으면 연산의 정의부터가 깔끔하게 딱 떨어지지 않고 굉장히 골치 아파진다. 내 기억이 맞다면 나머지의 부호는 나누는 수의 부호와 동일한 것이 원칙일 텐데, 당장 컴퓨터의 정수 나머지 연산은 그렇지 않다. 걔들은 부호 불문하고 몫은 그냥 소숫점을 짤라낸 것이고, 나머지는 그 몫으로부터 파생된 부산물이기 때문이다.
또한 bit shift 연산에서도 음수만치 shift한 결과는 그냥 undefined가 된다. a<<(-b)가 자동으로 a>>b로 되는 게 아닌 게 의외이다.
그럼 음수는 나머지나 비트 shift 같은 정수 컴퓨터 연산에서만 복병인가 하면 그렇지 않다. 일반적인 대수학에서 거듭제곱의 영역으로 가 봐도 음수는 난감한 상황을 만들어 낸다.
가장 먼저, 제곱해서 음수가 되는 수 자체가 통상적인 실수 중에는 존재하지 않는다. 이런 수는 도대체 특성이 어떤 놈일까? 이런 개념을 처음으로 떠올리고 고안한 사람은 도대체 무슨 부귀영화를 바라고 무슨 약을 빨고 이걸 생각해 낸 걸까?
지수함수의 정의역을 실수 전체로, 대수적으로 확장할 때도 음수는 애로사항이 꽃핀다. 당연히.. a^b에서 b 말고 a가 음수인 것 말이다. 음수의 거듭제곱은 횟수에 따라서 부호가 음수와 양수 사이를 널뛰기 하듯 바뀌는데, 그 횟수 자체가 자연수를 넘어 다른 이상한 수가 된다면 결과가 도대체 어떻게 되겠는가?
지수함수를 대수적으로 확장한 결과에 따르면, 음수에 대해 정수가 아닌 거듭제곱을 한 결과는 허수가 섞인 복잡한 복소수가 된다. (-1)^(1/2)는 당연히 그 정의상 i가 되고 말이다.
0과 1은 그 어떤 수로 거듭제곱을 시켜도 다른 정상적인 형태의 수가 나오지 않는다. 그렇기 때문에 이 두 수는 로그 함수의 base가 될 수 없다.
하지만 복소수 범위에서는 0과 1만 빼고 나머지 아무 복소수라도, 음수와 심지어 -1조차도 log의 밑이 될 수 있다. -1을 삐리리 승 하면 100이 될 수 있고 1000이 될 수도 있다는 뜻이다. 단지 그 수가 실수가 아닌 복소수 중에 있을 뿐이다. -1의 거듭제곱은 그냥 -1과 1 사이만 진동할 거라고? 천만의 말씀이다.
다만 정의역을 실수로만 한정하면 x에 대해서 Re((-1)^x)의 그래프.. 쉽게 말해 -1의 x승의 실수부는 cos(Pi*x)의 그래프와 같으며, 허수부를 나타내는 Im((-1)^x)의 그래프는 sin(Pi*x)의 그래프와 완전히 같다! 애초에 x^n=1의 근이 복소평면에서 정다각형의 꼭지점 형태로 나타나니, 거듭제곱과 삼각함수는 피할 수 없는 귀결이라 하겠다.
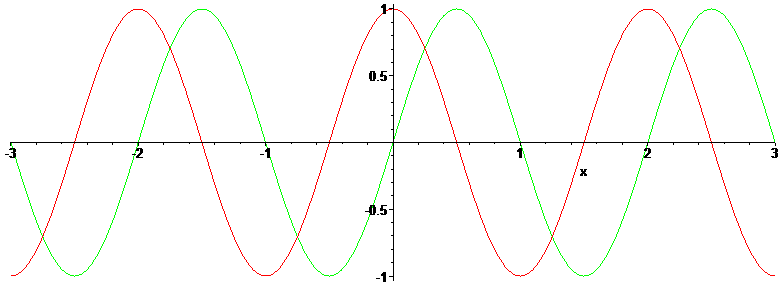
어째서 그렇게 되는지는 너무 어렵게 생각할 것 없이 그 유명한 오일러의 등식 정도만 따져 봐도 된다. 우리는 고등학교 수준에서는 로그를 그냥 실수 범위까지만 배웠겠지만, 그것이 그림의 전부가 아니다.
또한, 정의역을 실수로만 한정했을 때 이렇다는 것이고, 다른 임의의 복소수를 주면 (-1)^x는 절대값이 1보다 더 큰 다른 수도 얼마든지 나올 수 있다.
a^x를 넘어 아예 x^x의 그래프를 복소수 범위까지 생각해서 그려 보면 더 환상적인 결과를 얻을 수 있다.
얘는 양의 실수 범위에서는 x=1/e일 때 최소값을 갖는다. x=0일 때는.. 0의 0승이기 때문에 값을 구하기가 좀 아햏햏하긴 하지만 극한값이 양쪽 모두 1이기도 하고, 많은 경우에 0^0은 여느 수의 0승과 마찬가지로 1이라고 편의상 통용되곤 한다.
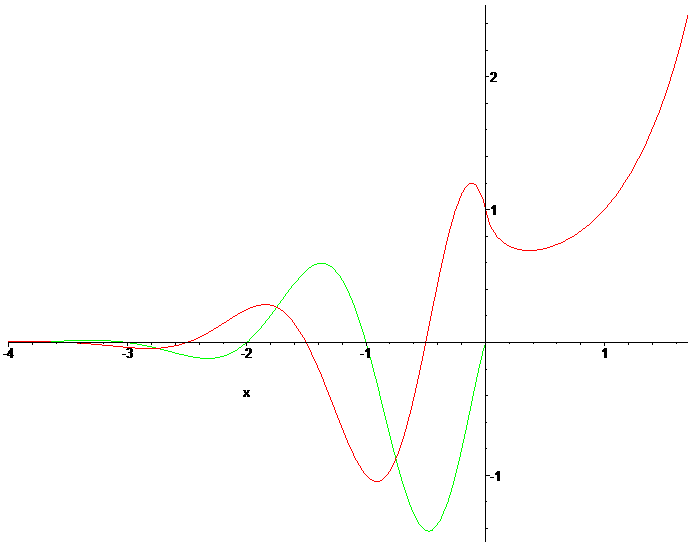
하지만 x가 본격적으로 음수가 되면.. 이제 그래프는 실수 영역에 존재하지 않게 된다. 뭐, 어차피 실수부와 허수부 모두 0으로 급격하게 쪼그라들기 때문에 생각만치 볼 건 없긴 하다만... 그래프의 모양이 꽤 예술적이어 보이지 않는가? =_=;;
수학에는 수에서 특정 부분의 정보를 떼어내고 남은 부분만 되돌리는 연산자 내지 함수가 세 가지 남짓 있다.
(1) 가장 먼저, 수에서 부호를 제거하는 ‘절대값’이 있다. 여닫는 세로줄 기호는 다들 친숙할 것이다. y=|x|는 오르내리는 사선을 만들어 낸다.
얘는 복소수를 대상으로는 복소평면에서 원점으로부터의 거리를 의미하기도 하며, 행렬에서는 행렬식을 의미하기도 한다.
(2) 그리고 수에서 소수점을 떼어내고 근처의 정수를 되돌리는 floor 내지 ceiling 연산이 있다. 얘는 그래프에서 계단을 만들어 낸다.
(3) 끝으로, 복소수에서 실수부 내지 허수부만을 되돌리는 Re() 및 Im()이 있다.
이런 연산들은 다 특정 분야에서 인간에게 필요하고 특정 관점에서 의미가 있기 때문에 고안된 것이겠지만.. 미적분 같은 해석학의 관점에서 자연스럽고 직관적인 연산은 결코 아니다. 절대값 연산은 부호가 바뀌는 지점에서 미분 가능하지 않은 지점을 만들며, 소수점 자르기는 더 나아가 아예 연속이지도 않은 지점을 만든다.
멀쩡한 복소수에서 실수부나 허수부만 떼어내는 것도 저 그래프의 예쁘고 매끄러운 모양과는 달리, 만만찮게 인위적이고 부자연스러운 보정이다. 그렇기 때문에 x^x에서 x가 음수일 때 실수부와 허수부의 그래프 식을 따로 구해서 각각 최대값과 최소값까지 구하는 건 양수일 때와 같은 방법으로 할 수 없다. 복소함수를 취급하는 더 복잡하고 난해한 방법론을 동원해야 한다.
복소수라는 개념을 떠올리고 나니까 어째 리만 가설이라는 것도 나올 수 있고 20세기엔 수렴· 발산 여부로 만델브로트니, 줄리아니 하는 프랙탈 집합까지 발견할 수 있었다. 이런 걸 도대체 어떻게 찾아냈을지 오묘하기 그지없다. 다들 계산량이 엄청나고 빡세다는 공통점도 있다. 하긴, 프랙탈이 '차원'이라는 개념도 대수적으로 확장했다. 행렬 계산의 최적 시간 복잡도에서 거듭제곱 계수가 2도, 3도 아닌 로그함수 값이 된 것처럼 말이다.
이상이다.
리만-제타 함수라든가 감마 함수 같은 난해한 함수들이 양수 구간과 음수 구간이 모양이 심하게 차이가 나고, 특히 음수 구간에서는 상하로 심하게 널뛰기를 하는 근본 이유가.. 지수 함수와 관련된 음수의 기괴한 특성 때문이라고 감을 잡으면 될 듯하다.
x^x 말고 0의 x승의 경우.. 양수에 대해서는 그냥 0이 될 것이고 0^0은 사실상 1이 통용되고 있고, 음수 승은 0으로 나누는 것과 동급인 부정으로 귀착된다.
Posted by 사무엘


