일명 “4색 정리, 4색 문제”는 개념 자체는 마치 페르마의 마지막 정리처럼 초등학생도 이해할 수 있을 정도로 아주 단순하다. 하지만 엄밀한 증명은 20세기의 현대 수학자조차도 감당하지 못할 정도로 난해했던지라, 1976년이 돼서야 컴퓨터의 brute-force 계산 능력의 도움을 받아 간신히 증명됐다.
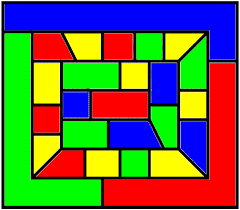
요즘으로 치면 무슨 머신 러닝을 돌리듯이 당대의 슈퍼컴 두 대를 장정 50일을 돌리면서 가능한 모든 지도 모델에서 증명이 성립함을 확인했다고 한다.
물론 저건 오늘날의 머신 러닝에 비할 바는 못 된다. 내 기억이 맞다면, 1970년대 중반의 크레이 슈퍼컴퓨터는 20여 년 뒤에 등장하여 클럭 속도가 GHz급에 도달한 펜티엄 3~4급 PC와 얼추 비슷한 성능이었다. 요즘 PC라면 GPU 세팅만 잘 하면 하루는커녕 길어야 수십 분~몇 시간이면 시뮬레이션이 끝나지 싶다. 그만치 세상이 많이 변했다.
하지만 1976년은 지금으로부터 무려 45년 가까이 전의 과거이다. 증명할 지도 모델을 설계하고 계산량을 그 시절 컴퓨터로 감당 가능하게 최소화한 것만으로도 독창적인 학술 공로이며, 대학교 수학과 교수 급의 전문가가 아니면 할 수 없는 일이었다.
또한 극도로 비싸고 귀하신 몸이던 슈퍼컴을 당장 실용적으로 필요하던 일기예보나 모의 핵실험, 탄도 예측(?)이 아닌 학술 연구용으로 끌어들여 온 것 역시 해당 연구자의 행정력과 근성과 로비 덕분이었던 셈이다.
한편, 정사각형을 크기가 서로 다른 작은 정사각형들로 분할하는 문제(lowest-order perfect squared squares)도 굉장히 난해하지만 답이 존재는 하는 굉장히 기묘한 문제인데.. 4색 정리와 비슷하다면 비슷한 시기인 1978년에 길이 112짜리 사각형을 21개로 분할하는 해법이 발견됐다. 이 역시 컴퓨터를 동원하여 찾아낸 것이었다.
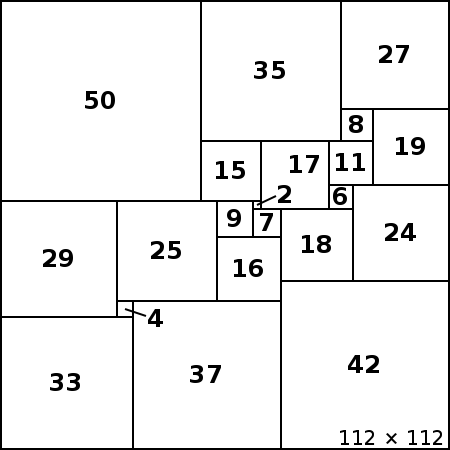
또한, 저 정사각형들도 최대 4개의 색만으로 서로 경계를 구분하여 칠할 수 있을 테니, 이것도 4색 문제하고 관계가 있다고 볼 수 있겠다. =_=;;
1982년에는 동일 연구자의 후속 연구를 통해 저게 이론적으로 존재 가능한 optimal 내지 lower bound라는 것도 증명됐다. 즉, 20개 이하의 서로 다른 정사각형으로 큰 정사각형을 꽉 채우는 방법은 존재하지 않는다는 것이다.
다만, 가장 작은 정사각형 분할의 하한은 112가 아니라 110이라고 한다. 분할 개수는 21개보다 딱 1개 더 많은 22개이다. 참으로 신기한 노릇이다.
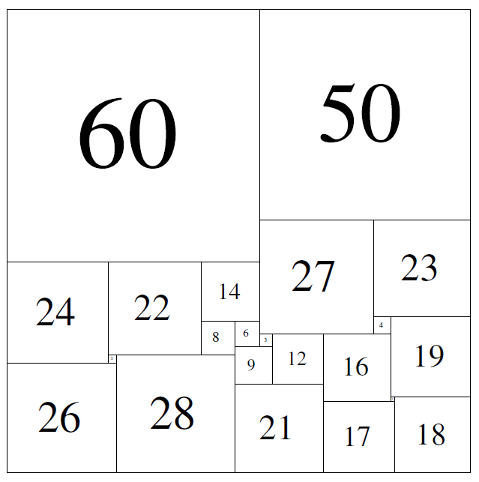
그 전에 컴퓨터의 도움 없이 사람이 찾아낸 가장 단순한 정사각형 분할은 175를 24개로 분할하는 것이었다. (81, 55, 39, …) 1946년에 데오필루스 윌콕스(1912-2014)라는 영국 사람이 발견했다.
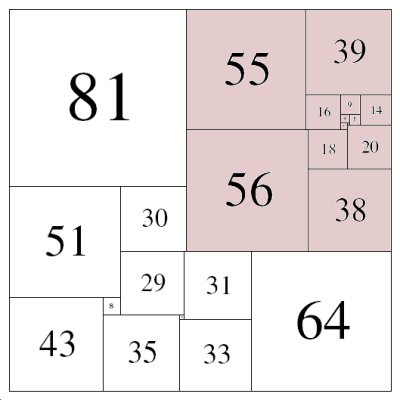
정사각형을 서로 다른 정사각형으로 분할하는 방법 자체는 다양한 크기별로 무한히 존재하기라도 하는지? 이게 증명돼 있기라도 한지는 모르겠다. (자명한 닮은꼴은 물론 제외. 작은 정사각형의 크기값들이 모두 서로 소인 것으로 한정)
단지 2차원이 아니라 3차원에서 정육면체를 서로 크기가 다른 정육면체로 꽉 맞게 채운다거나 그 이상의 차원에서 같은 방법으로 hypercube를 채우는 방법은 아예 존재하지 않는다고 한다.
직관적으로 생각해도 명확한 것이... 3차원만 생각해 봐도 그런 정육면체가 있다면 여섯 면이 다 제각기 크기가 서로 다른 정사각형으로 거대한 정사각형을 이룬 모습을 기본적으로 하고 있어야 할 것이다. 하지만 정육면체만으로 그렇게 되는 것은 불가능하기 때문이다.
벡터의 외적이 딱 3차원 벡터에 맞게 존재하는 이항연산이듯이, a^n+b^n=c^n의 정수해가 존재하는 n의 상한이 딱 2인 것처럼.. 정사각형 분할은 딱 2차원 평면에서 존재 가능한 절묘한 문제인 것 같다.
Posted by 사무엘


