자연에서 중력이 만들어 내는 물체의 '운동 궤적'은 이차함수 포물선이다. 중력이 물체를 아래로 일정하게 가속시키기 때문이며, 이는 심지어 총알 같은 작고 가볍고 빠른 물건이라도 예외가 아니다. 지구에서는 그나마 공기의 저항이란 게 있어서 그 포물선의 말단 부분이 더 가팔라지는 것을 막아 준다.

한편으로, 중력이 자연스럽게 만들어 내는 '물체의 선형'은 현수선이다. 밀도가 동일한 줄, 선, 사슬 따위를 양 끝을 잡아서 매달았을 때 그 줄이 자연스럽게 축 늘어진 모양 말이다. 이건 포물선이나 타원(!!) 따위가 아니라 수학적으로 완전히 다른 선형이다.

포물선은 공중으로 내던져진 물체가 붕 떠올랐다가 떨어지는 궤적이다. 그렇기 때문에 운동 궤적 말고 자연에서 포물선이 쫙 그려지는 것은.. 글쎄, 불꽃놀이에서 불꽃이 자기 궤적 잔상을 남기면서 움직이는 모습 같은 게 아니면 보기가 쉽지 않을 것 같다.
그에 반해 현수선은 길다란 줄이 늘어져서 정지한 모습 그 자체이기 때문에 어쩌면 포물선보다도 더 친근한 모습일 수 있다.
포물선은 이차함수이며 원뿔곡선에 속하는 반면, 현수선은 답부터 말하자면 더 생소하고 어려운 쌍곡선함수, cosh이다. 왜 그렇게 되는 것이며 이 함수가 지니는 의미는 무엇일까?
일단 쌍곡선함수라는 것 자체가 중등 교육과정에는 등장하지 않는다. 그리고 현수선의 원리를 제대로 설명하려면 고전역학 지식이 필요하며, 식을 유도하려면 역시 중등에서는 배우지 않는 미분방정식이라는 걸 풀어야 한다.
하지만 꼭 그 정도로 엄밀하게 따지지 않더라도 cosh가 될 수밖에 없는 대략의 이유 정도는 중등 수준만으로도 납득할 수 있다.
현수선은 외형상 명백하게 중력이 작용하는 아래로(y축 값이 작아지는 쪽) 볼록하면서 좌우가 대칭인 곡선이어야 할 것이다.
현수선 공식을 유도하는 여러 사이트들의 설명은 대체로 비슷하다. 선 내부에 있는 임의의 점에 대해.. x축으로 작용하는 힘은 좌우가 모두 동일한 반면(그래야 합력이 0으로 상쇄되고 안정되므로), y축으로 작용하는 힘은 자연스러운(= 줄이 향하는 방향) 상하뿐만 아니라 양쪽 줄의 무게까지 감안했을 때 합력이 0이 된다는 것이다.
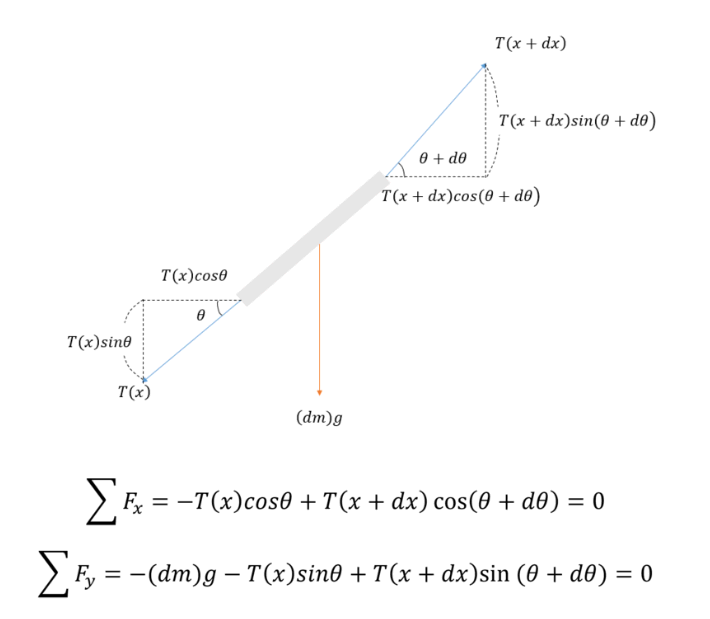
그래서 선의 정체에 대한 결론은 다음과 같은 형태의 미분방정식으로 귀착된다.
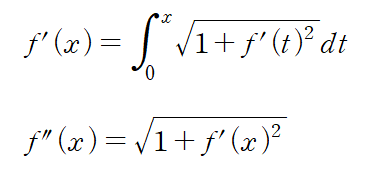
이게 의미하는 게 무엇일까?
이 f(x)는 어떤 점 x에서의 기울기(좌변)가 0부터 x까지 f(x) 함수 곡선의 거리(우변)와 동일 내지 상수배 정비례한다는 뜻이다.
양변을 한번 더 미분하면 아래처럼 되지만, 2차 도함수(도함수의 변화량을 나타내는 도함수..)는 머리로 이해하기가 더 난감하다.
그럼 sqrt(1+f'(x)^2)라는 거리 적분식은 어디서 왜 나오는가..? 줄의 무게가 줄의 길이에 정비례하기 때문이다.
x축 지점에 대한 도함수에다가 그 지점까지 선의 길이에 대한 함수값을 대입하면 식이 그렇게 나오게 된다.
도함수 f'(x)가 x 자체와 같은 함수 f(x)는 x의 부정적분인 x^2 /2 + C ... 즉 포물선이 된다.
f'(x)가 f(x)와 같은 함수는.. e^x, 즉 지수함수이다.
그 반면 f'(x)가 거리 적분과 같은 함수는 중력이 작용하는 임의의 지점에서 역학적 평형을 이루는 현수선이 된다는 것이 핵심이다. 그리고 이 미분방정식을 풀면 이 f(x)는 cosh가 된다.
cosh는 맞은편 쌍곡선함수인 sinh와 짝이며, 미분· 적분을 하면 상대방으로 곧장 바뀐다. cos/sin처럼 부호가 바뀌면서 4행정(?) 순환을 하는 것도 아니고 그냥 2행정이다. 그렇기 때문에 cosh는 2차 도함수도 자기 자신과 같다.
그 말인즉슨... f(x)는 어디에서든 길이의 증가폭과 면적의 증가폭이 동일한 함수라는 뜻도 된다! y=x 같은 직선은 이 조건을 만족하지 않는다. x가 커지면 길이는 일정하게 증가하더라도 아래의 면적은 제곱으로 증가하기 때문이다.
그리고 cos^2 + sin^2 = 1이듯이 쌍곡선함수는 cos^2 - sin^2 = 1이다.
sqrt( 1 + f'(x)^2 )에서 f(x)에다가 cosh(x)를 집어넣으면 f'(x)^2는 sinh(x)^2가 되는데, 얘는 저 정의에 따라 cosh(x)^2 - 1로 치환 가능하다. 그러니 -1은 앞의 1과 상쇄되어 없어지며, 제곱은 제곱근과 상쇄되어 없어지니...
찰나의 거리 변화량을 구하는 함수가 자기 자신과 동일해지는 것이다!
예전에 란체스터의 법칙 얘기를 하면서도 쌍곡선함수가 나왔는데, 얘가 비록 삼각함수보다 인지도가 떨어지지만 나름 자기 분야에서 유용한 구석이 있음을 알 수 있다.
Posted by 사무엘


