김 용묵의 절대공간 - 블로그

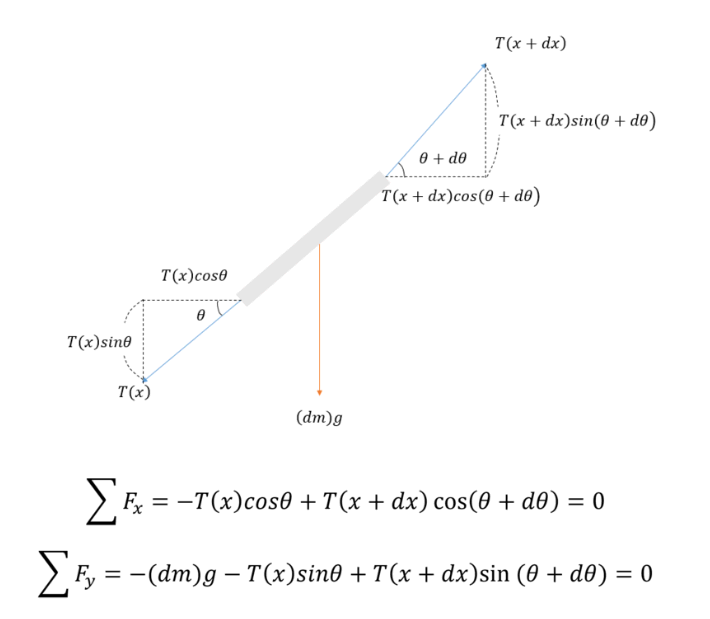
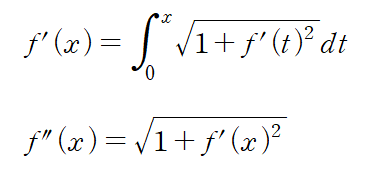우리 주변에서 교량(다리)이라는 건축물들을 보면 (1) 교각이라고 불리는 기둥들이 물 위에 일정 간격으로 박혀 있고, 그 교각들을 한데 잇는 길이 위에 놓여 있다. 그 이상 딱히 다른 특이사항은 없다.

하지만 어떤 교량은 추락· 투신을 방지하기 위한 난간의 규모 이상으로 (2) 거대한 철골 구조물(트러스? 아치?)이 놓여 있다. 자동차보다 훨씬 더 무거운 열차가 다녀서 그런지 한강철교가 이런 형태이다. 그 밖에 서울 지하철이 다니는 동호대교(3호선)과 동작대교(4호선)도 이런 범주에 들며, 특히 후자는 동그란 아치 모양의 철골 구조물이 있다.

다만, 모든 철교가 이런 형태인 건 아니다. 그리고 철골 구조물이 그냥 다리 하부에 상판과 기둥 사이에 설치된 것도 있다. 성수대교 내지 구 당산철교(부실 시공 붕괴 위험으로 인해 1997년에 철거됨)가 그 예이다.

경부 고속도로의 초기 개통 구간 중에는 비록 강을 건너는 건 아니지만 아래의 지형을 훌쩍 타넘는 고가 교량이 몇 군데 있었다. 대전 육교와 당재 육교가 대표적인데, 미관을 살리고 아래에 차지하는 공간도 최소화하기 위해 교각이 아치 형태로 만들어졌다. 1960년대 말에는 이 정도 건축물을 만드는 것도 굉장히 어렵고 위험한 일이었다.

그 다음으로 대형 교량 중에는 (3) 다리의 기둥을 아득히 초월하는 높은 주탑이 세워져 있고, 다리 상판이 케이블에 매달린 형태인 게 있다. 신기하지 않은가?

사장교는 상판의 각 지점이 주탑과 직통으로 연결돼 있다. 그래서 주탑으로부터 덕지덕지 뻗은 케이블은 직선 모양이다. 서울에서는 올림픽대교가 사장교의 유명한 예이며, 서울과 인천 공항을 연결하는 인천대교, 그리고 당진과 평택을 잇는 서해안 고속도로의 서해대교도 사장교이다.

그 반면 현수교는 양 주탑이 주케이블로 연결돼 있고, 주케이블에 일정 간격으로 매달린 보조 케이블들이 상판들을 지탱하는 형태이다. 그렇기 때문에 주케이블의 선형은 곡선이다.
영종대교, 부산의 광안대교, 울산의 울산대교가 현수교이다.

샌프란시스코의 금문교(Golden Gate)는 현수교의 상징이나 마찬가지이다. 1940년에 바람에 흔들려 요동치다가 붕괴된 걸로 유명한 미국의 타코마 다리 역시 현수교였다.
현수교는 현존하는 다리들 중 기둥 사이 간격을 압도적으로 제일 멀리 벌릴 수 있는 형태이다(거의 2km 이상도).

울산대교는 인도가 존재하지 않는 자동차 전용 도로 교량임에도 불구하고 지난 몇 년간 주행 중에 차에서 갑자기 내려서 뛰어내리는 자살 시도자 때문에 골머리를 앓고 있다고 한다. 하지만 거기에다 무슨 마포대교 같은 급의 거대한 난간과 자살 방지 시설을 추가로 설치하는 건 불가능하다. 케이블이 상판을 지탱하는 현수교의 특성상, 다리가 버틸 수 있는 하중이 무한하지 않기 때문이다.

사장교와 현수교는 경제성 및 안정성 면에서 제각기 장단점이 있다. 사장교는 주탑이 하나만 있어도 되지만 현수교는 그 특성상 적어도 둘 이상 필요하다.
한강의 하류 서울 시내 구간은 폭이 1km 남짓이니 강치고는 굉장히 큰 편이지만, 그래도 사장교라면 모를까 현수교가 필요할 정도의 길이는 아니라고 여겨진다.
사장교와 현수교의 차이를 한눈에 쏙 들어오게 그림으로 묘사하면 다음과 같다.

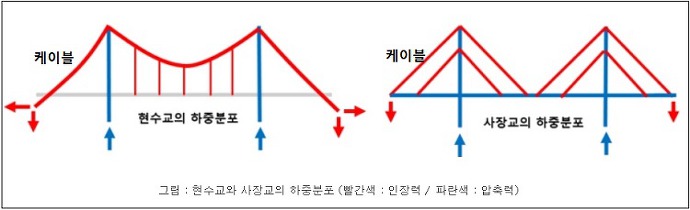
자, 이렇게 (1)뿐만 아니라 (2)나 (3) 유형의 다리가 있는 이유는 무엇일까? 특히 바다를 건너는 길이 수 km짜리 거대한 교량은 굳이 엄청나게 높은 주탑까지 세우면서 (3)과 같은 형태로 만드는 이유가 무엇일까?
그저 미관과 폼 때문에? 그렇지 않다. (2), 특히 (3)은 같은 무게를 지탱하는 다리라도 “기둥 수를 최소화해서” 만들려는 노력의 결과물이다.

자잘한 기둥 여러 개를 그냥 커다란 주탑 하나와 케이블로 퉁치는 게 더 저렴하다는 것, 콘크리트 구조물이 그냥 물도 아닌 바닷물 소금물에 쩔어서 좋을 건 하나도 없으니 적을수록 좋다는 것 따위는 부수적인 이유이다. 무엇보다도 다리 아래로 일정 규모 이상의 큰 선박이 지나갈 공간이 있어야 하기 때문이다. 이건 강이 아닌 바다 위의 교량이라면 진지하게 고려해야 할 사항이 된다.

과거에는 이럴 때 자동차와 선박의 건널목 평면교차나 마찬가지인 도개교를 만드는 게 유행이었다. 하지만 요즘은 기술의 발달로 인해 다리 자체를 엄청 크고 높게 만들고 말지, 교통수단 간의 평면교차는 만들지 않는 추세이다.
이렇게 다리의 유형 종류를 알고 나면 다음에 자동차나 열차로 다리를 건널 일이 있을 때 이 다리는 어떤 방식인지를 더 주의 깊게 보게 될 것이다.

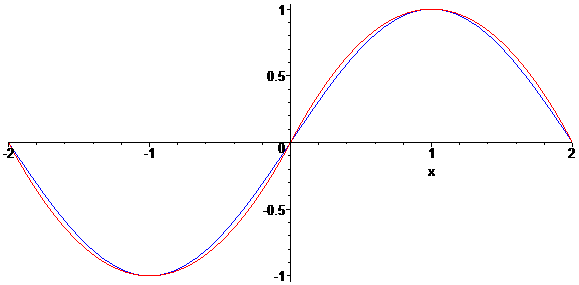
현수교와 관련해서는 꽤 의외의 사실이 있다. 현수교의 주케이블이 자연스럽게 형성하는 선은 현수선이 아니다.
그냥 자연스럽게 매달려 있기만 할 때는 현수선이지만, 일정 간격으로 주렁주렁 매달린 보조 케이블로부터 힘을 받으면서 유사품(?)인 포물선에 가깝게 변형된다.

그 이유는 의외로 간단하다.
현수선은 걸리는 무게가 선 자체의 길이에 비례해서 커진다.  그렇기 때문에 이전에 살펴본 바와 같이 미분 방정식에 거리 적분이 들어갔으며, 이게 cosh라는 함수의 근원으로 작용했다.

그러나 현수선 아래에 하중이 걸리는 것은 선 자체의 길이나 기울기와 전혀 무관하게 그냥 x축의 일정 간격으로 균일하게 힘이 가해지는 것이다. 그러면 미분 방정식이 f(x) = x 급으로 아주 간단해지며, 문제의 함수는 포물선을 그리는 이차함수로 귀착된다.

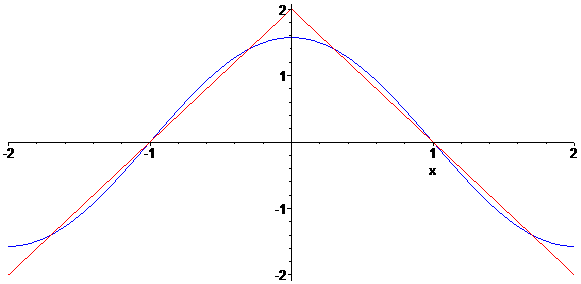
다만, 선형이 완벽하게 포물선이 되기 위해서는 걸리는 하중이 띄엄띄엄이 아니라 연속적으로 일정하게 걸려야 하며, 줄 자체의 무게는 걸리는 하중과 비교했을 때 무시할 수 있을 정도로 없다시피해야 한다.
그렇지 않은 현실에서는 선형이 현수선과 포물선 사이의 어중간한(?) 모양이 되겠지만.. 포물선과 현수선은 특정 조건을 만족하는 한도 내에서는 어차피 서로 매우 비슷한 모양이라고 여겨진다.

1600~1700년대에 고전 역학과 미적분학이란 게 처음 생겨나던 시절에는 뉴턴, 호이겐스, 베르누이, 라이프니츠 같은 당대의 날고 기는 수학자들 사이에서도 이 궤적이 포물선일까 현수선일까 긴가민가 하는 경우가 있었다. 그 시절엔 충분히 헷갈릴 만도 했다는 생각이 든다.;;

Posted by 사무엘

자연에서 중력이 만들어 내는 물체의 '운동 궤적'은 이차함수 포물선이다. 중력이 물체를 아래로 일정하게 가속시키기 때문이며, 이는 심지어 총알 같은 작고 가볍고 빠른 물건이라도 예외가 아니다. 지구에서는 그나마 공기의 저항이란 게 있어서 그 포물선의 말단 부분이 더 가팔라지는 것을 막아 준다.

한편으로, 중력이 자연스럽게 만들어 내는 '물체의 선형'은 현수선이다. 밀도가 동일한 줄, 선, 사슬 따위를 양 끝을 잡아서 매달았을 때 그 줄이 자연스럽게 축 늘어진 모양 말이다. 이건 포물선이나 타원(!!) 따위가 아니라 수학적으로 완전히 다른 선형이다.

포물선은 공중으로 내던져진 물체가 붕 떠올랐다가 떨어지는 궤적이다. 그렇기 때문에 운동 궤적 말고 자연에서 포물선이 쫙 그려지는 것은.. 글쎄, 불꽃놀이에서 불꽃이 자기 궤적 잔상을 남기면서 움직이는 모습 같은 게 아니면 보기가 쉽지 않을 것 같다.

그에 반해 현수선은 길다란 줄이 늘어져서 정지한 모습 그 자체이기 때문에 어쩌면 포물선보다도 더 친근한 모습일 수 있다.
포물선은 이차함수이며 원뿔곡선에 속하는 반면, 현수선은 답부터 말하자면 더 생소하고 어려운 쌍곡선함수, cosh이다. 왜 그렇게 되는 것이며 이 함수가 지니는 의미는 무엇일까?

일단 쌍곡선함수라는 것 자체가 중등 교육과정에는 등장하지 않는다. 그리고 현수선의 원리를 제대로 설명하려면 고전역학 지식이 필요하며, 식을 유도하려면 역시 중등에서는 배우지 않는 미분방정식이라는 걸 풀어야 한다.
하지만 꼭 그 정도로 엄밀하게 따지지 않더라도 cosh가 될 수밖에 없는 대략의 이유 정도는 중등 수준만으로도 납득할 수 있다.

현수선은 외형상 명백하게 중력이 작용하는 아래로(y축 값이 작아지는 쪽) 볼록하면서 좌우가 대칭인 곡선이어야 할 것이다.
현수선 공식을 유도하는 여러 사이트들의 설명은 대체로 비슷하다. 선 내부에 있는 임의의 점에 대해.. x축으로 작용하는 힘은 좌우가 모두 동일한 반면(그래야 합력이 0으로 상쇄되고 안정되므로), y축으로 작용하는 힘은 자연스러운(= 줄이 향하는 방향) 상하뿐만 아니라 양쪽 줄의 무게까지 감안했을 때 합력이 0이 된다는 것이다.

그래서 선의 정체에 대한 결론은 다음과 같은 형태의 미분방정식으로 귀착된다.

이게 의미하는 게 무엇일까?
이 f(x)는 어떤 점 x에서의 기울기(좌변)가 0부터 x까지 f(x) 함수 곡선의 거리(우변)와 동일 내지 상수배 정비례한다는 뜻이다.
양변을 한번 더 미분하면 아래처럼 되지만, 2차 도함수(도함수의 변화량을 나타내는 도함수..)는 머리로 이해하기가 더 난감하다.

그럼 sqrt(1+f'(x)^2)라는 거리 적분식은 어디서 왜 나오는가..? 줄의 무게가 줄의 길이에 정비례하기 때문이다.
x축 지점에 대한 도함수에다가 그 지점까지 선의 길이에 대한 함수값을 대입하면 식이 그렇게 나오게 된다.

도함수 f'(x)가 x 자체와 같은 함수 f(x)는 x의 부정적분인 x^2 /2 + C ... 즉 포물선이 된다.
f'(x)가 f(x)와 같은 함수는.. e^x, 즉 지수함수이다.
그 반면 f'(x)가 거리 적분과 같은 함수는 중력이 작용하는 임의의 지점에서 역학적 평형을 이루는 현수선이 된다는 것이 핵심이다. 그리고 이 미분방정식을 풀면 이 f(x)는 cosh가 된다.

cosh는 맞은편 쌍곡선함수인 sinh와 짝이며, 미분· 적분을 하면 상대방으로 곧장 바뀐다. cos/sin처럼 부호가 바뀌면서 4행정(?) 순환을 하는 것도 아니고 그냥 2행정이다. 그렇기 때문에 cosh는 2차 도함수도 자기 자신과 같다.
그 말인즉슨... f(x)는 어디에서든 길이의 증가폭과 면적의 증가폭이 동일한 함수라는 뜻도 된다! y=x 같은 직선은 이 조건을 만족하지 않는다. x가 커지면 길이는 일정하게 증가하더라도 아래의 면적은 제곱으로 증가하기 때문이다.

그리고 cos^2 + sin^2 = 1이듯이 쌍곡선함수는 cos^2 - sin^2 = 1이다.
sqrt( 1 + f'(x)^2 )에서 f(x)에다가 cosh(x)를 집어넣으면 f'(x)^2는 sinh(x)^2가 되는데, 얘는 저 정의에 따라 cosh(x)^2 - 1로 치환 가능하다. 그러니 -1은 앞의 1과 상쇄되어 없어지며, 제곱은 제곱근과 상쇄되어 없어지니...
찰나의 거리 변화량을 구하는 함수가 자기 자신과 동일해지는 것이다!

예전에 란체스터의 법칙 얘기를 하면서도 쌍곡선함수가 나왔는데, 얘가 비록 삼각함수보다 인지도가 떨어지지만 나름 자기 분야에서 유용한 구석이 있음을 알 수 있다.

Posted by 사무엘

퇴근길에 문득 든 아주 기초 수학 생각이다.
아래 그림은 포물선 2개 x^2+2*x (x=-2..0), -x^2+2*x (x=0..2)와, sin(x*PI/2) (x=-2..2)를 한데 포개 놓은 것이다.
원래 sin, cos 부류의 삼각함수는 주기가 2*PI인데, 이를 4로 좁혀 놓았다.
이렇게 보니까 포물선도 싸인파 곡선과 형태가 생각보다 꽤 비슷해질 수 있다는 걸 느꼈다.

0부터 2까지 구간의 넓이를 정적분으로 구해 보면 이차함수인 포물선의 면적은 4/3인 반면, 진짜 싸인파의 면적은 4/PI이다. 즉, 포물선에 속하는 면적이 약간 더 크다.

그러나 이 두 곡선은 비슷하게 생겨도 그 본질은 굉장히 다르다. 미분을 해 보면 안다. 이들의 도함수를 그래프로 그리면 다음과 같다.

싸인파는 도함수도 기준 위치와 진폭만 다를 뿐, 여전히 전구간이 미분 가능한 매끄러운 싸인파이다.
그러나 두 포물선을 인위적으로 연결한 함수는 도함수가 직선으로 바뀌었고, x=0 지점은 연속이긴 하지만 기울기의 좌극한과 우극한의 값이 서로 달라서 미분이 불가능한 점이 되었다. 마치 절대값이 들어있는 일차함수처럼 된 셈이다.

이걸 또 미분하면 어떻게 될까?
싸인파는 역시 또 싸인파이지만 저 직선은 아예 양수 아니면 음수의 상수함수로 바뀌고, x=0 지점은 이제 연속이지도 않게 된다. 마치 인간이 만든 아무리 매끄럽고 뾰족한 바늘도 확대하고 또 확대해서 보면 울퉁불퉁한 표면이 드러나듯이 말이다.

우리가 자연에서 흔히 볼 수 있는 물체의 운동 양상은 관성에 의한 등속 직선, 아니면 힘을 한 쪽으로 균일하게 받는 포물선 형태가 있다. 하지만 출렁이는 물결이나 음파 같은 진동은 삼각함수에 속하는 싸인파가 자연스러운 움직임이다. 오히려, 포물선 두 개를 갖다붙인 것에 불과해서 미분하면 딱딱한 절대값 직선으로 바뀌어 버리는 곡선이야말로 인위적이고 부자연스러운 형태인 것이다.

왜 싸인파가 자연스러운 움직임일까?
삼각함수는 무한소나 무한대로 발산하지 않고 주기를 갖고 -1에서 1 사이를 한없이 진동만 한다.
그러면서도 전구간이 단절 없이 연속이고 미분 가능하다. 미분을 해도 심지어 도함수조차 형태를 바꾸면서 주기적으로 자기 자신으로 돌아오기를 반복하기 때문이다.
내가 수학적인 통찰력이 부족해서 그 원리를 다 '이해'와 '실감'은 못 하겠지만, 적어도 이런 함수는 돼야 정말 매끄러움의 본질을 수학적으로 표현한 게 아닌가 하는 막연한 추측까지는 한다.

해석학적으로 볼 때 x^n의 x에 관한 미분은 n*x^(n-1)로 떨어진다. 지수함수 exp는 알다시피 (1/ n!)*x^n의 무한합으로 정의되어, x에 대해 미분하더라도 예전항이 바로 다음항의 미분 결과와 같은 꼴이 되는 형태이다.

그런데, 삼각함수인 sin과 cos는 exp를 홀수승 항과 짝수승 항으로 분할함과 동시에 각 항의 부호를 또 +, -로 교대로 오고 가게 바꾼 형태이다. 그래서 함수가 무한대나 무한소로 발산하지 않고 진동하게 된다. 신기하기 그지없다.

미적분학을 공부하면 삼각함수와 더불어 쌍곡선함수라는 물건도 배우게 된다.
얘는 sin과 cos에다가 h를 붙여서 sinh, cosh처럼 쓰는데, 지수함수를 이루는 무한급수에서 각각 홀수승항과 짝수승항만 쪼개서 취한 함수이다. 삼각함수와의 차이는 부호 스위칭이 없다는 점이 전부다.

그래서 쌍곡선함수는 비록 그래프의 모양은 삼각함수와 완전히 다르지만 삼각함수와 굉장히 비슷한 특성을 갖게 된다. sinh와 cosh는 미분하면 부호 스위칭이 없이 서로 상대편으로만 탈바꿈하며, 삼각함수의 덧셈정리와 비슷한 특성도 가진다. 삼각함수가 cos(x)^2 + sin(x)^2 = 1이듯이 cosh(x)^2 - sinh(x)^2 = 1이다. 전자가 원스럽다면 후자는 정말 쌍곡선스러운 형태이지 않은가?

쌍곡선함수는 사실상 수학 해석학적인 의미 때문에나 배우지, 삼각함수에 비해 실생활에서 유용한 구석은 별로 없는 것 같다. 그러나 얘도 자연에서 의외로 중요한 곳에서 자주 볼 수 있다. cosh가 바로 현수선의 방정식을 나타내는 함수이기 때문이다.

현수선이란 밀도가 균일한 줄이 자기 길이보다 짧은 간격으로 양 끝이 어떤 중력장 안에 매달렸을 때, 자신의 무게로 인해 중력의 방향(아래)으로 축 늘어짐으로써 형성되는 선을 말한다.
이것도 포물선과 비슷해 보여서 혼동되기 쉽지만, 포물선하고는 수학적인 성질이 완전히 다르다. 현수선은 증가의 폭이 이차함수가 아니라 지수함수와 같은 스케일이다.

알고 보면 아치도 포물선이 아니라 현수선을 뒤집은 모양이다. 현수선 모양으로 구조물을 건설하는 게 모양이 역학적으로 가장 안정적으로 형성된다고 한다.
왜 현수선이 cosh 함수의 형태로 형성되는지 수학적으로 증명하려면 물리학, 미적분학 등 여러 방면의 이론이 동원돼야 하지 않을까 싶다.

어찌 보면 당연한 말이지만, 현수선은 일부만 잘라 내도 그 모양이 그대로 유지된다. 다시 말해 U자 모양으로 된 현수선의 양 끝의 일부를 잘라내서 u부분만 잡고 있더라도 기존 부위가 받는 힘은 변함없으며, 그 구간의 선 모양이 바뀌지 않는다는 뜻이다.

삼각함수와 쌍곡선함수가 각자 자기 분야에서 포물선과는 다른 매끄러움, 출렁거림 등을 표현하고 있다는 게 경이롭다.
자연 현상으로부터 얻은 물리량이라는 게 태생적으로 연속적인 데이터의 형태이다 보니, 물리학의 발전을 위해서는 수학, 특히 미적분학의 발전이 반드시 선행되어야 했다는 게 느껴진다.

Posted by 사무엘

수학에서 함수라는 것은 y=f(x)와 같은 형태로, x에다가 임의의 수를 대입하면 그에 대응하는 y 값이 계산을 통해 딱 하나로 산출되어 나오는 관계를 말한다.

하지만 f(x, y)=0라고 함수를 정의할 수도 있다.
이 식을 만족하는 x, y가 곧 정의역과 치역임이 규정된다.
이런 형태의 함수를 수학 용어로는 음함수(implicit function)라고 일컫는다.
딱 명시적인 함수 형태는 아니지만 함수를 암시적으로 규정하고 있다는 뜻인데, ‘음’이라고 하면 negative가 먼저 떠올라서 한국어로는 뜻이 잘 와 닿지 않는 것 같다.

음함수가 표현력이 더욱 풍부하다. 그도 그럴 것이 y=sqrt(1-x^2)라고만 하면 사분원반원 하나밖에 표현을 못 하지만, x^2+y^2=1이라고 하면 원 전체를 표현할 수 있기 때문이다.
그리고 컴퓨터 상으로 음함수를 처리하는 것도 더욱 까다롭다. x뿐만 아니라 x와 y를 2차원적으로 모두 고려해야 하기 때문이다. 2차원만으로 모자라서 z축도 동원하여 3차원까지 가면 흠..;;;

고등학교 시절에는 이런 음함수 중에서 x, y의 계수가 최대 2차까지 갈 수 있는 녀석을 배운다. 일반화하면 아래와 같은 꼴.

a*x^2+ b*x*y+ c*y^2+ d*x+ e*y+ f = 0

2차식인 a, b, c중 적어도 하나가 0이 아니라면 이 음함수는 아래의 형태 중 하나가 된다.

1. x, y가 실수 범위에서 전혀 존재하지 않기 때문에 빈 그래프. (x^2+y^2=-1 같은 경우)
2. 두 직선 (x^2-y^2=0 같은 경우. 또한, xy=0 이라고 하면 x축과 y축^^)
3. 타원 (x^2+y^2=1)
4. 쌍곡선 (x^2-y^2=1)
원이나 포물선은 굉장한 레어 케이스에서나 존재 가능하다.
또한, a, b, c 계수의 관계에 따라 곡선의 모양이 어떻게 될지 알려주는 판별식도 있다.

2차 곡선인 이들 원, 타원, 포물선, 그리고 쌍곡선은 모습도 인간 세계에서 수학적인 의미를 두기에 충분한 가치를 지니고 있다. 모래시계처럼 ▶◀ 형태로 놓인 원뿔의 단면을 잘랐을 때 나오는 곡선이라고 해서 원뿔곡선(conic section)이라고도 불린다. 신기한 일이 아닐 수 없다.

짤방은.. 초점이 동일한 어느 타원과 쌍곡선의 모습을 자작 프로그램으로 그린 것. 나름 안티 앨리어싱까지 되어 보기에 더욱 아름답다. ㅋ

타원은 “한 초점에서의 거리 + 다른 초점에서의 거리”가 일정한 점들의 집합이다. 두 초점에다가 실을 묶고 팽팽하게 연필을 그으면 비교적 쉽게 그릴 수 있다.
원은 두 초점의 위치가 일치하는 특수한 경우라 하겠다. 타원 모양으로 된 당구대 안에서 그 타원의 한 초점에서 공을 굴리면, 그 공은 다른 초점을 반드시 지나게 될 것이다.

쌍곡선은 “한 초점에서의 거리 - 다른 초점에서의 거리”의 절대값(=차이)이 일정한 점들의 집합이다. 절대값이다 보니 필연적으로 곡선이 둘 존재한다. 초등학교 시절에 배웠던 y=1/x 반비례 그래프가 알고 보니 이 쌍곡선이었다는 사실을 알게 된다.

포물선이야 중학교 시절에 제곱근과 2차식이라는 개념 자체를 처음으로 접할 때 배운다. 그런데 포물선은 단순한 2차식을 넘어서 “한 초점과 한 기준선이 주어졌을 때 초점에서의 거리와 준선까지의 수직 최단 거리가 일치하는 점들의 집합”으로 다른 관점에서 정의가 이루어진다. 사실, 타원과 쌍곡선도 한쪽 초점이 한없이 멀어지면 포물선 모양으로 수렴하게 된다.

포물선은 중력이 존재하는 지구상에서 물건을 던지기만 해도 매우 쉽게 볼 수 있다(단, 공기 저항이 없어야). 포물면은 반사하는 모든 빛을 초점으로 한데 모을 수 있다. 다만, 만들기가 구면보다는 어렵다.

2차 곡선은 이렇듯 세상에서 쉽게 볼 수 있고 실용적이다. 거리와의 제곱에 비례해서 감소하는 만유인력과도 관계가 있다. 제곱의 의미는 2차원, 즉 면적이다.
인공위성은 흔히 지구를 향해 한없이 추락하는 물체라고들 한다. 공중에서 충분한 추진력으로 위성을 가속하지 못하면 그 발사체는 지구로 떨어져 버린다. 그러나 속력이 어느 정도 빨라진 순간부터는 이제 지구로 떨어지지 않고 원 궤도를 그리게 된다.

더 빨라지면 위태위태 타원 궤도를 그리게 되고, 어느 정도 도를 넘어서면 포물선, 그 이후부터는 쌍곡선 궤도를 그리면서 그 발사체는 지구로 다시는 돌아오지 않게 된다. 옛날에 이런 거 시뮬레이션 프로그램을 장난감 삼아 짜면서 놀았던 기억이 있다. ^^;;

그 반면에 음함수의 식이 3차까지 가면, 모양만 변태적으로 복잡하지 쓸모가 없다. 변수의 값이 어떻냐에 따라서 쌍곡선 같은 그런 곡선이 3쌍둥이가 생기기도 하고, -⌒- 이런 모양이나 아니면, 그런 모양에 U자 모양 곡선이 합쳐진 놈 등... 자연에서 볼 일도 없고 의미가 없다는 것이다.

앞서 음함수를 처리하는 건 쉬운 일이 아니라고 언급했는데, 실제로 그렇다.
정확하게 일치하지는 않겠지만 윤곽선 폰트를 래스터라이즈하는 일과 비슷한 과정이 아닐까 하는 생각이 든다.
무식하게 x*y개의 함수값을 일일이 다 구해 보지 않고도 함수값을 구성하는 영역만 매끄러운 경계선을 추출하고 거기에다 안티 앨리어싱까지 하는 건 보통 어려운 일이 아니다.

아래아한글이나 포스트스크립트 같은 다른 폰트 시스템은 잘 모르겠지만, 윈도우 운영체제가 사용하는 트루타입 폰트 래스터라이저는 매 도트에 대해서 윤곽선 안에 있는지의 여부를 판단해서 글자를 찍어 낸다. 그래서 힌팅 정보가 없으면 작은 글씨에서 가는 획이 아예 화면에서 사라지는 일이 생길 수 있다.

본인은 옛날에 너무나 깔끔하게 잘 출력되는 영문 폰트들을 보고서 트루타입 폰트 래스터라이저가 굉장히 똑똑한 줄 알았는데, 알고 보니 다 아주 정교한 수작업으로 만들어진 힌팅 정보 덕분이었다. 힌팅은 획의 굵기를 일관성 있게 보정할 뿐만 아니라 윤곽점을 래스터라이저가 글립 존재 여부를 판단할 때 사용하는 위치로 강제로 옮겨서 획이 사라지지 않게 하는 역할도 한다.
흠, 글 주제가 수학에서 폰트 얘기로 급반전.. 어쨌든 음함수의 렌더링도 그만치 쉬운 일은 아니라는 뜻이다. ^^;;

Posted by 사무엘