수학에서 행렬은 굉장히 흥미로운 물건이다.
행렬끼리의 덧셈이나 행렬의 상수배는 어려울 게 없는 쉬운 연산이지만, 행렬끼리의 곱셈은 그렇지 않다. 행렬 A와 B사이의 곱셈은 A의 가로 크기와 B의 세로 크기가 같아야 정의되며, 새로 생기는 행렬의 크기(dimension)는 반대로 B의 가로 크기와 A의 세로 크기로 결정된다.
이런 특성상 행렬의 크기는 세로, 즉 row부터 먼저 써 주는 게 직관적이다. 세로 x줄 가로 y줄짜리 x,y 행렬과 y,z 행렬의 곱은 x,z 크기가 된다고 표기가 가능하기 때문이다.
또한, 앞에 있는 행렬과 뒤에 있는 행렬이 원소가 서로 연산되는 방향이 다르기 때문에 행렬의 곱셈은 교환 법칙이 성립하지 않는다. A×B가 일반적으로 B×A와 같지 않다는 뜻. 그러나 결합 법칙은 성립한다. (A×B)×C와 A×(B×C)는 동일하므로, 같은 방향만 유지하면 아무 순서로나 행렬을 곱해 줘도 된다.
그래서 이것과 관련하여 흥미로운 문제가 하나 있다.
크기가 들쭉날쭉 다르지만 순서대로 곱셈은 가능한(= 인접한 행렬끼리는 앞 행렬의 가로 크기와 뒤 행렬의 세로 크기가 일치) N개의 행렬들이 있다. 우리는 이들을 모두 최소의 계산량만으로 곱하고 싶다.
역행렬이나 행렬식 값을 구하는 비용에 비할 바는 아니겠지만 행렬의 곱셈은 꽤 비싼 연산이다. 일반적으로 x,y 크기와 y,z 크기의 행렬을 곱하는 데는 원소들간에 x*y*z회의 곱셈이 필요하다. n 크기의 정사각행렬의 경우 이는 n^3으로 귀착된다. (뭐, 분할 정복법을 활용하여 n^2.x승으로 줄이는 복잡한 알고리즘이 있긴 하지만 이것은 초기 준비 오버헤드가 굉장히 크기 때문에 행렬이 무진장 클 때에나 의미가 있다.)
예를 들어 A는 4*2 크기, B는 2*3 크기, C는 3*1크기의 행렬/벡터라고 치자.
이것을 A*B*C 순으로 진짜 순서대로만 곱하면 A*B를 곱하는 데 4*2*3=24회의 곱셈이 동원되고, 그 결과물인 4*3 행렬을 C와 곱하느라 12회의 곱셈이 필요해서 계산량은 총 36이 된다.
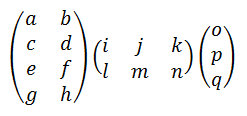
그러나 B*C부터 먼저 곱한 뒤 A를 거기에다 곱하면 열수가 적은 C 덕분에 B*C는 겨우 6회 만으로 끝나고, 거기에다 4*2*1=8회의 곱셈이 추가되어 총 14의 계산량만으로 A*B*C를 구할 수 있다. 답은 결국 똑같은데도 (AB)C보다 A(BC)가 훨씬 더 나은 전략인 것이다.
신기하지 않은가? 그래서 이런 configuration을 일반화하여 {4, 2, 3, 1}이라고 표현하고, 더 나아가 n>=3인 n개의 자연수라고 치자.
이 입력에 대해서 최소 곱셈 횟수와 실제 곱셈 순서를 구하는 것이 문제이다.
정올 공부를 한 분이라면 아시겠지만, 이것은 다이나믹 프로그래밍, 혹은 동적 계획법이라는 알고리즘 설계 방법론을 학습하면서 예시로 다뤄지는 아주 기본 문제이다. 다이나믹 프로그래밍은 다음과 같은 경우에 유용하다.
- 전체 구간에 대한 최적해가 부분 구간의 최적해에다가 추가 연산을 함으로써 구하는 게 가능하다.
- 그리고 한번 답을 구해 놓은 부분 구간의 최적해는 더 바뀌지 않는다는 게 보장된다.
이 행렬의 곱셈 문제에서 가장 작은 구간은 3이며, 이때의 답은 그냥 두 말할 나위 없이 세 정수의 곱이다.
그리고 전체 구간 [1..n]에 대해서 최적해는 바로..
- 1을 [2..n]과 곱했을 때의 계산량 (맨 앞의 행렬과 나머지)
- [1..n-1] 과 n을 곱했을 때의 계산량 (앞의 행렬들과 맨 뒤의 행렬)
중 더 작은 놈이라고 간주하면 된다.
그럼 [2..n]과 [1..n-1]은? 각 구간에 대해서 또 동일한 해법을 적용하여 재귀적으로 구간을 계속 쪼개 나가는 것이다. 언제까지? 구간의 길이가 3이 될 때까지 말이다.
이렇듯, 다이나믹 프로그래밍은 재귀성을 띠고 있다. 이것은 수학적으로는 점화식으로 표현되며, 코드로는...
const int dat[]={4,2,3,1,2,6,5,8,3,2}; //배열
int GetMin(int f, int t)
{
int i=t-f, j;
if(i<3) return 0; //should not reach here
else if(i==3) return dat[f]*dat[f+1]*dat[f+2]; //obvious case
else {
//사실은 i가 3인 경우도 이 조건의 특수한 케이스라고 간주할 수 있다.
//단지 GetMin값이 0이고, t-2와 f+1이 동일한 값이 될 뿐이다.
i=GetMin(f,t-1) + dat[f]*dat[t-2]*dat[t-1]; //(A*B)*C
j=GetMin(f+1,t) + dat[f]*dat[f+1]*dat[t-1]; //A*(B*C)
return i<j ? i:j;
}
}
int answer = GetMin(0, 10);
과연 이렇게 하면 답이 구해질까?
프로그램을 돌려 보면, 10개의 정수로 표현된 9개의 서로 다른 크기의 행렬들의 곱은..
146회의 곱셈만으로 계산이 가능하다고 나온다.
구체적인 계산 순서는 이러하다.
4 (2 (3 (((((1 2 6) 5) 8) 3) 2)))
이 경우, 각 단계별 계산 순서는 다음과 같이 되기 때문에,
| x | y | z | x*y*z |
| 1 | 2 | 6 | 12 |
| 1 | 6 | 5 | 30 |
| 1 | 5 | 8 | 40 |
| 1 | 8 | 3 | 24 |
| 1 | 3 | 2 | 6 |
| 3 | 1 | 2 | 6 |
| 2 | 3 | 2 | 12 |
| 4 | 2 | 2 | 16 |
곱을 전부 합하면 진짜로 146이 맞다!
참고로, 이런 전략을 쓰지 않고 진짜 FM대로 앞에서부터 뒤로 행렬을 순서대로만 곱하면 계산량은 최적해의 세 배를 넘는 492에 달한다.
이것이 바로 알고리즘이 만들어 내는 차이이다.
다이나믹 프로그래밍에는 반드시 수반되어야 하는 작업이 있다. 바로 예전에 구했던 구간 계산값들을 배열에다 저장해 두는 것이다. 그렇게 하지 않으면, 마치 피보나치 수열을 f(x) = f(x-1)+f(x-2)라고만 구현하는 것만큼이나 계산량이 n이 커짐에 따라 기하급수적으로 커지게 된다. 그것도 예전에 한번 했던 똑같은 계산을 매번 반복하느라 말이다.
그래서 이 방법을 사용한 알고리즘은 대체로 시간 복잡도와 공간 복잡도가 모두 O(n^2)이 된다. 시간 복잡도가 지수함수에서 그래도 다항함수로 바뀐다.
구간별로 최적해 자체뿐만이 아니라 구간 분할을 어떻게 했는지에 대한 정보도 따로 보관해 놓으면 아까와 같은 구체적인 계산 순서도 그 정보를 추적함으로써 구할 수 있다.
정올에서 다이나믹 프로그래밍의 중요성은.. 두 말하면 잔소리이다.
본인은 20세기에 정올 공부를 한 세대인지라 그 시절의 문제밖에 기억을 못 한다만..
1997년 한국 정보 올림피아드의 고등부 3번인 벽장 문제는 최적해를 구하고자 할 경우 공간과 시간 복잡도가 O(n^3)인 다이나믹 프로그래밍으로 풀 수 있다. 이 때문에, 16비트 환경임을 감안하더라도 이 문제는 입력의 범위가 작다. 벽장의 개수와 벽장 사용 순서가 최대 겨우 20까지밖에 안 올라가는 소규모이다. 실용적인 상황에서는 이런 부류의 시뮬레이션 문제는 휴리스틱이 동원되어야 할 것이다.
이 외에,
1999년 고등부 1번 검은 점 흰 점 연결,
2000년 고등부 1번 수열 축소
도 다이나믹으로 푸는 문제이다.
국제 정보 올림피아드의 기출 문제 중에는
10회(1998)의 둘째 날 마지막 문제인 폴리곤 게임,
11회(1999)의 첫째 날 첫 문제인 꽃 진열이 기억에 남는다. 특히 꽃 진열은 상당히 기초적인 다이나믹 프로그래밍 문제로, <날개셋> 타자연습의 문장 정확도 측정도 이와 거의 같은 발상의 알고리즘을 사용하고 있다.
난 이 바닥은 손 놓은 지가 너무 오래 돼서 기억이 가물가물하다.
정보 올림피아드에서 경시와 공모는 마치 과학과 공학, 어학과 문학의 차이와 비슷한 것 같다.
Posted by 사무엘


