A와 B라는 두 집단이 서로 패싸움을 시작했다. A는 전투원이 5명이고 B는 4명이다. 그런데 양 진영의 모든 전투원들은 체력· 정신력· 무장 등등이 완전히 동일하며, 기습 가능성이라든가 지형적인 유불리, 엄폐물 같은 것도 없이 탁 트인 개활지에서 순수하게 힘과 힘만이 충돌하는 형태로 싸우게 됐다고 치자. 싸움은 둘 중 한 진영의 전투원들이 몽땅 죽거나 중상을 입어서 전투력을 상실할 때까지 계속된다. 그렇다면 이 싸움의 결과는 어찌 될까?
마오 쩌둥이던가 스탈린이던가.. 인권 쌈싸먹은 독재자답게 "전쟁 나서 1억 인구가 죽는 것쯤은 별 일 아니다. 사람이야 또 낳으면 되니까. 적군이 병력이 1억이면 우리는 1억에다 한 명만 더 붙여서 이기면 된다" 그런 요지의 무지막지한 말을 한 적이 있었다. 정확하게 누가 언제 한 말인지 출처 확인이 잘 안 되네, 분명 본 기억은 있는데..
그런데 저건 병신 같지만 묘하게 설득력이 있는 말이다. 외적인 요인이 차이가 전혀 없고 완전히 동일하다면 상식적으로 생각했을 때 쪽수가 한 명이라도 더 많은 집단이 필승하고 부족한 집단은 필패할 것이다.
위의 경우라면 B가 지고 A가 이기는 것 자체는 따 놓은 당상이다. 단지 문제는 A가 B를 얼마나 너끈히 이기느냐, 어느 정도의 피해를 입고 승리하느냐로 귀착된다.
그 답은 A와 B가 어떤 방식으로 싸우느냐에 따라 달라진다.
조폭들 패싸움처럼 기껏해야 일대일로 근접해서 냉병기를 사용하는 싸움이라든가, 총이라 해도 18세기 전열보병 전술처럼 비현실적일 정도로 너무 신사적으로 일대일 턴제로 싸우는 거라면 말 그대로 일대일로 상쇄하고 남은 병력만이 생존자가 된다. B는 전멸이요, A는 A-B에 해당하는 인원이 남는다. 고로 5:4의 싸움이라면 한 명만 남는 거다. 이것을 일명 란체스터 제1법칙이라고 한다.
그러나 점 vs 점이 아니라 면 vs 면 단위로 실시간으로 부딪치는 현실의 전투에서는 다구리가 더 대규모로 가능하며 병력의 작은 차이가 훨씬 더 큰 차이를 야기한다. 설정상 한 집단의 전투력은 병력에 비례해서 나오게 돼 있는데 그 전투력 자체가 병력의 손실로 인해서 차츰 감소한다. 두 변수가 같이 변화하면서 비선형적인 구도를 만든다는 뜻이다. 그래서 처음부터 병력과 전투력이 열세였던 집단은 그 감소폭이 더욱 커지면서 전멸에 이르지만, 우세 집단이 받는 대미지는 시간이 흐를수록 더욱 작아진다. 전투력도 부익부 빈익빈으로 치닫는다!
그래서 답부터 말하자면, 이런 현실의 싸움에서 A와 B가 붙으면 B가 전멸한 뒤 A는 한 명만 남는 게 아니라 이론적으로 3명이나 생존해 있게 된다. B는 자기 진영 4명이 전멸하는 동안 A를 2명밖에 못 죽인다는 것이다. 공식으로 표현하면 단순한 A-B가 아니라 sqrt(A^2 - B^2)이다.
마치 직각삼각형 세 변의 길이와 같은 구도가 된다. 그렇다면 5명 vs 4명이 아니라 13명 vs 12명이 붙으면, 12명 팀은 전멸하고 13명 팀은 8명만 죽어서 5명이 남는다.
이것은 란체스터 제2법칙이라고 명명되어 있다. 영국의 항공 공학 엔지니어가 1차 세계 대전의 양상에서 착안하여 고안했다.
스타크 같은 전략 시뮬 게임에서 드라군, 마린, 히드라 같은 원거리 공격 유닛들을 서로 마주보게 해서 어택 땅으로 싸움을 붙여 보면 이 법칙이 의외로 굉장히 잘 적중한다고 한다. 란체스터의 법칙에 대해 소개해 놓은 타 블로그 글들을 검색해 보면 전략 시뮬 게임으로 실험을 해 봤는데 높은 적중률을 보고 놀랐다는 말이 많이 나온다. 1억 명에다가 딱 한 명만 더 보태서 이기면 된다는 말이 그저 허세만은 아닌 셈이다.
란체스터 제2법칙이 어째서 성립하는지를 엄밀하게 논하려면 삼라만상의 변화량을 기술하는 끝판왕 도구인 미분방정식을 동원해야 한다.
시각 t에 대해서 A 진영의 병력을 나타내는 함수 f(t), B 진영의 병력을 나타내는 함수 g(t)를 정의하자.
위의 예에서는 전투 전의 초기 상태 t=0에 대해 f(0)=5, g(0)=4가 될 것이다. 뭐, 일반화해서 f(0)=a, g(0)=b라고 잡아도 된다.
전투의 진행으로 인해 f(t), g(t) 모두 병력이 감소할 것이다. 그런데 그 감소하는 변화량이 바로 상대방 함수의 함수값과 같다. d f(t) / dt = -g(t) 요, d g(t) / dt = -f(t)라는 뜻이다.
그렇다면 이 f와 g는 도대체 어떻게 생겨먹은 함수일까? 0보다 큰 t에 대해서 g(t)=0이 되고(B 진영의 전멸) 그 정의상 동시에 f'(t)=0도 되는 지점이 있을 것이다. 그 t가 얼마인지는 중요하지 않겠지만, 이때 f(t)의 값을 a와 b에 대해서 구하면 란체스터 제2법칙을 유도할 수 있을 것이다.
f의 도함수가 -g이고 g의 도함수가 또 -f라니.. 일단 얘는 미분을 짝수 번 반복하면 도함수가 자기 자신으로 돌아오는 뭔가 골때리는 함수 형태가 될 듯하다. 즉, 4배수 주기로 제자리로 돌아오는 삼각함수보다는.. cosh, sinh 같은 쌍곡선함수 형태가 될 것 같다. 걔들은 미분을 하면 cosh, sinh, cosh ... 이렇게 반복되는데, 문제의 저 함수는 f, -g, f, ... 이렇게 반복된다.
그래서 답을 구해 보면.. a>b여서 f가 더 우세한 진영을 나타낸다는 걸 염두에 뒀을 때
2*f(x) = (a+b)/e^x + (a-b)*e^x 요, 2*g(x) = (a+b)/e^x - (a-b)*e^x 가 된다. (2를 곱한 게 저런 것이므로 전체를 2로 나눠 줄 것)
e^x와 e^x의 역수를 절반씩 적절히 더하거나 빼는 cosh / sinh 함수를 상수배/평행이동만 한 형태인 걸 알 수 있다. f는 cosh에 대응하고 g는 그냥 sinh가 아니라 -sinh가 된다.
cosh는 현수선을 나타내는 함수이기도 하다. 그 말인즉슨 A와 B가 싸울 때 A의 피해 양상은 빨랫줄이나 쇠사슬이 아래로 축 늘어진 것과 비슷한 양상으로 스무스하게 감소할 거라는 뜻이다. 실제로 그런지 확인해 보자.
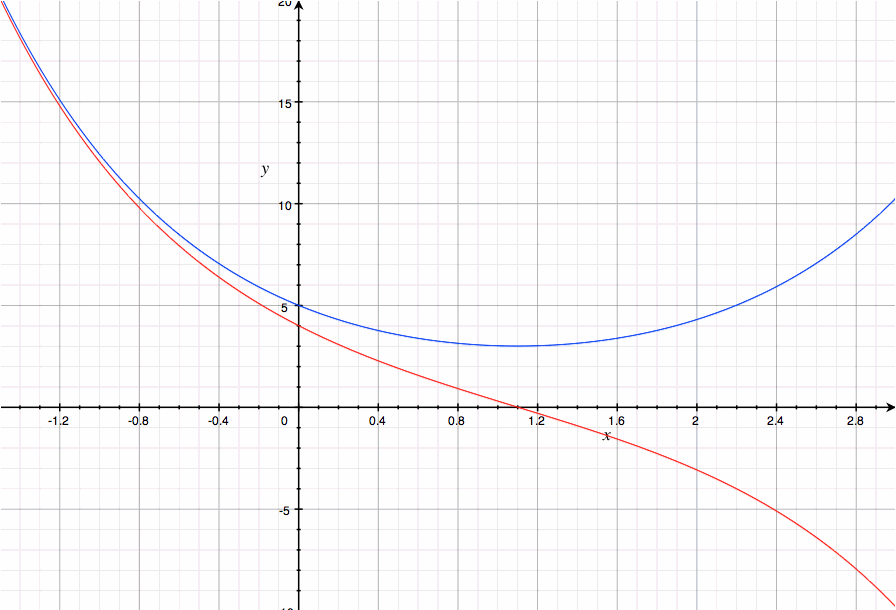
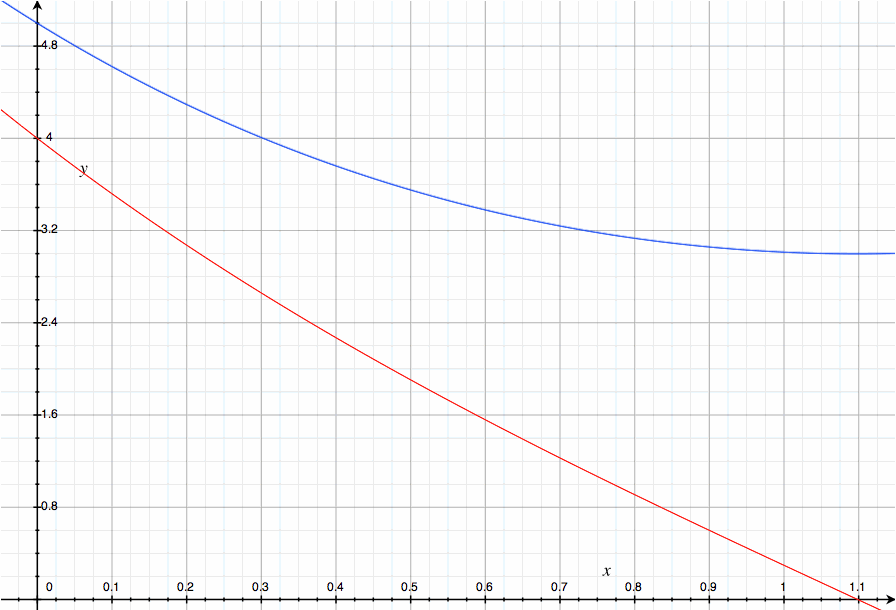
g(x)=0이 되는 시점은 x= ln( (a+b)/(a-b) )/2 가 되며, (a=5, b=4일 때는 저 값은 대략 1.1)
이때 f(x)를 구해 보면 (a+b)/sqrt( (a+b)/(a-b) )가 나오고 식을 정리하면 진짜로 sqrt(a^2 - b^2)가 나온다.
임계점 이후부터는 g는 음수가 나오고 f는 감소가 아니라 오히려 증가하기 시작하지만, 이건 현실에서는 아무 의미 없는 추세일 테니 제끼면 된다.
더 직관적인 비유로 설명하자면.. 5:4가 붙어서 곧이곧대로 1명만 남는 싸움, 즉 란체스터 제1법칙은 y=1이라는 상수 그래프를 떠올리면 된다. 여기서 x가 4부터 0까지 가는(B진영) 동일 면적(= 정적분)을 5에서부터(A진영) 시작한다면 1에 도달한다.
그러나 란체스터 제2법칙은 y=1이 아니라 y=x라는 가변적인 그래프에 대응한다. 여기서 x가 4부터 0까지 가는 B진영의 면적 8(밑변과 높이가 모두 4인 삼각형)을 5에서부터 시작한다면.. 1이 아니라 3에서 멈추게 된다. 윗변 3, 아랫변 5, 높이 2인 사다리꼴의 넓이가 8이 되니까 말이다.
이를 일반화하면, 0부터 B까지 y=x를 정적분한 값은 sqrt(A^2-B^2)에서부터 A까지 정적분한 값과 같다. 이렇게 이해해도 된다.
전쟁이라는 건 여기저기 가성비를 따지면서 지킬 것과 버릴 것을 가리고 작전을 잘 짜야 이길 수 있다. 즉, 경제· 경영과도 밀접한 관계가 있다. 그렇기 때문에 오늘날 란체스터의 법칙은 군사학보다는 경제학 쪽에서도 기초 이론으로 더 중요하게 다뤄진다. 포병 장교에다 수학 박사 출신인 지 만원 박사 같은 분이 아마 이런 분야의 최고 전문가가 아닐까 싶다.
이 법칙은 스플래시 데미지나 사이오닉 스톰-_- 같은 변수가 있지 않은 한, 왜 일반적으로는 "뭉치면 살고 흩어지면 죽는다"가 성립하는지를 무식하게 시행착오 겪을 필요 없이 수식만으로도 잘 설명해 준다. 5:4로만 붙여도 저 그래프와 같은 처참한 결과가 나오지 않던가?
더 나아가서 어지간히 절체절명의 위급한 상황이 아닌 이상, 스타에서 유닛이 생성되는 족족 적진으로 찔끔찔끔 축차투입을 해서는 절대 안 되며 캐리어 같은 유닛도 반드시 일정 기수 이상 모아야 제 성능이 발휘된다는 것을 보여준다.
또한 전쟁이 나면 전투 직전에야 양 진영이 모두 사기 진작이 매우 중요하기 때문에 "마지막 하나까지 결사항전" 운운하지만.. 대세를 도저히 뒤집을 수 없을 정도로 승부가 너무 기울고 100% 개죽음밖에 선택의 여지가 없을 때는 불가피하게 꼬리 내리고 항복도 하는 것이다.
이상. 란체스터 법칙 하나 갖고 미분방정식에, 쌍곡선함수에 별 얘기가 다 나왔다.
다만, 현실의 전장에서는 수학 숫자놀음 나부랭이보다 예측할 수 없는 외부 변수가 훨씬 더 많이 존재하기 때문에 란체스터 법칙이 절대적인 만능 장땡인 건 아니다. 겉으로 드러나는 병력 열세를 극복하고 B가 A를 이긴 사례도 역사엔 얼마든지 존재한다는 것도 생각할 필요가 있다.
그러니 성경에서 하나님께서 기드온에게 병사 수를 32000명에서 거의 1% 수준인 300명으로 일부러 줄여 버리고도 오히려 전투를 승리로 이끄신 것이 대단한 이야기인 것이다(삿 7). 진짜 300의 원조는 무슨 영화에 나오는 스파르타 군대가 아니라 저 군대였던 셈이다.
Posted by 사무엘


