두 초점 A, B가 있을 때 A에서의 거리와 B에서의 거리의 차가 동일한 점들의 집합을 쌍곡선이라고 한다. x^2 - y^2 = a 이런 음함수로 정의되며, 그래프를 그려 보면 곡선이 둘 그어지는 것이 특징이다.
그 반면, 합이 동일한 점들의 집합은 잘 알다시피 타원이며, x^2 + y^2 = a 꼴로 정의된다.
그런데 y=a/x, 다시 말해 xy = a 꼴인 반비례 함수는 x^2나 y^2처럼 단일 변수의 제곱이 존재하지 않는다. 하지만 우리는 이게 이차곡선인 쌍곡선의 표준형을 45도 돌린 형태라고 얼추 알고 있다.
어째서 그런 것일까? 수학적으로 더 엄밀히 증명해 볼 수는 없을까?
반비례 함수를 회전 행렬을 이용해서 45도 돌린 뒤, 이 함수가 쌍곡선 표준형과 동치임을 보이면 될 것이다.
45도일 때는 cos와 sin의 값이 sqrt(2)/2로 동일하다. 그렇기 때문에 (x, y)라는 점은 45도 회전하고 나면
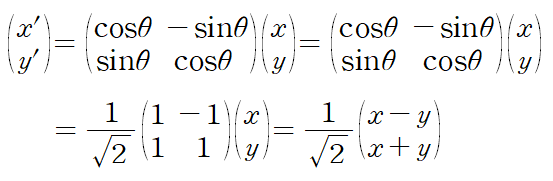
요렇게 된다. 그럼 다음으로 45도 돌아간 x', y'를 기반으로 우리의 목표인 쌍곡선 방정식을 재구성하면 된다.
그러면 기존의 x, y 변수를 없애야 하는데, 위의 식을 그대로 제곱해서 빼기만 해도 x'^2 - y'^2 = -2xy로 놀랍게도 x^2와 y^2이 소거되어 없어진다. 이는 앞서 살펴보았듯이 각도가 45도여서 cos와 sin의 함수값이 서로 동일한 덕분에 가능한 일이다.
마지막으로 남은 xy야 원래 반비례 그래프의 정의상 a로 치환하면 되니 금방 처리된다.
그러면 x'^2 - y'^2 = -2a가 되고 쌍곡선과 동일함이 입증된다. 뭔가 허무해 보이지만.. 이차곡선 중에서 x나 y의 제곱이 없는 식은 이렇게 쌍곡선으로 귀결된다.
45도가 아닌 다른 각도라면 기존 x, y가 이렇게 쉽게 소거되지 않기 때문에 문제가 이런 식으로 단순하게 풀리지 않게 된다.
가만히 생각해 보니, 애초에 Ax^2 + Bxy + Cy^2 + Dx+Ey+F = 0에 대해서 그래프의 모양을 결정하는 판별식도 있다. A,B,C 중 적어도 하나 이상은 0이 아닐 때, B^2 - 4AC가 0이면 이 그래프는 포물선이요, 음수이면 타원 또는 원, 양수이면 쌍곡선이 된다. 구체적인 유도 과정은 쉽지 않을 텐데.. 이거 정도면 중등 교육과정 범위에 있다.
그러니 xy=1이야 B만 비영이고 A, C는 0.. 판별식 값은 당연히 양수가 되고 쌍곡선으로 귀결된다. 오오~~
판별식의 형태가 1계수 이차방정식의 근 판별식과도 매우 유사하다. 이차방정식의 경우 A만 비영이라는 조건이지만, 이차곡선 내지 원뿔곡선 방정식의 판별식은 아까 상술하였듯이 A,B,C 중 아무거나 하나 이상만 비영이면 된다.
그리고 A부터 F까지 아무 숫자나 집어넣는다고 해서 원뿔곡선이 튀어나오는 게 아니다. 상수항이 0이거나 하면 원이 극도로 작아져서 그냥 점이 되기도 하며, 쌍곡선은 점근선을 나타내는 직선 두 개로 귀착된다. 당장 xy=0만 해도 x축과 y축을 동시에 나타나내는 직선이 되니까.. 그럼 다음으로 포물선은..? 평행한 두 직선이 돼 버린다.
이차방정식이 x^2+1 = 0 같은 경우 실수 근이 존재하지 않는 것처럼.. 이것의 이변수 상위 호환인 원뿔곡선 방정식도 실수 범위에서 공집합이 될 수도 있다.
이 개념을 degeneracy(축퇴.. 축 쪽으로 퇴화)라고 부른다. 뭔가 행렬에서 행렬식의 값이 0이 돼 버리는 상황 같은 느낌이 들지 않는가? 계수가 주어졌을 때 축퇴 여부를 판별하는 판별식도 있다. 이건
(b^2-4ac)f + ae^2 - bde + cd^2
으로, 곡선 종류 판별식을 포함하면서 다소 복잡한 편이다. 이걸 유도하는 건 확실하게 중등 이상의 더 어려운 영역이며, 더 추상적인 수학 개념이 동원된다. 딱 봤을 때 각 항들에 변수가 2개가 아니라 3개씩 곱해진 것부터가 매우 인상적이다.
쌍곡선에서 시작해서 이차곡선에 대한 더 원론적인 얘기로 주제가 옆길로 좀 샜는데.. 다시 쌍곡선 얘기를 하며 글을 맺겠다.
반비례 그래프는 xy=a, 즉 x의 역수를 구하는 함수인지라 y=-x의 그래프에 대칭인 쌍곡선이 튀어나온다. e^x가 도함수가 자신과 동일한 함수라면, a/x는 역함수가 자신과 동일한 함수이다. f(f(x)) = x가 성립하는 게 어찌 보면 not이나 xor 연산 같아 보이기도 하다..
원의 방정식이 그 정의상 (cos(t), sin(t))라는 매개변수로 표현될 수 있는 것처럼 쌍곡선의 방정식은 (cosh(t), sinh(t))라는 매개변수로 표현될 수 있다. cosh와 sinh의 배치가 바뀌면 쌍곡선의 위치가 상하 또는 좌우로 바뀐다.
그리고 원의 방정식이 y=sqrt(a-x^2) 같은 꼴로 양함수로 표현될 수 있는 것처럼 쌍곡선의 방정식은 y=sqrt(x^2+a)의 꼴로 표현될 수 있다. a의 부호가 무엇이냐에 따라 쌍곡선의 배치(상하 또는 좌우)가 바뀐다. 한편으로 저 모양만 봐도 x의 값이 너무 작거나 커지면 y=x에 가까워질 소지가 다분해 보임을 알 수 있다.
Posted by 사무엘



