1. 증가 양상 변화
코딩을 하다 보면... 0부터 1 사이에 있는 속도, 압력, 밝기 등 자연계의 다양한 아날로그 신호를 입력으로 받았는데 그걸 있는 그대로 곧이곧대로 처리하는 게 아니라, 특정 구간(특히 중앙)이 더 부각되어 인지되도록 비선형적으로 보정해야 할 때가 있다. 그 구간을 if문으로 따로 분리하는 건 좀 무식해 보이니, 가능하면 함수 형태로 스무쓰하게 처리되게 하는 게 좋을 것이다.
이런 처리의 대표적인 예로는 화면의 '감마 보정'(gamma correction)이 있다.
일반 사용자의 입장에서는 이건 막연히 화면의 밝기를 조절하는 기능으로 보인다. 하지만 이건 단순히 모든 색들의 RGB 값을 일괄적으로 올리는 게 아니다. 양 극단의 제일 어둡거나 밝은 색은 그냥 놔 두고, 어중간하게 어두운 색들의 명도를 올려서 화면이 전반적으로 선명하게 보이게 해 준다.
모니터가 브라운관이든 LCD든 오래되면 그렇잖아도 어중간한 색깔을 표현하는 능력이 떨어지니, 감마 보정이 화질의 개선에 도움이 된다.
그리고 애초에 사람의 눈도 밝기를 그렇게 선형적으로 인식하지 않는다고 한다. 흑백 그러데이션을 그냥 선형적인 색 변화로만 늘어놓으면 색깔띠가 밝은 부분보다는 어두운 부분이 더 부각돼 보인다. 이때 적절히 감마 보정을 하면 흑백과 회색 구간이 그럭저럭 균형 잡혀 보이게 된다.

그럼 이 감마 보정은 어떻게 하는 걸까?
정의역 0~1, 치역 0~1, f(0)=0, f(1)=1이고 증가량의 차이만 있을 뿐 단조증가 자체는 보장되는(전구간에서 도함수의 값이 0 이상이 보장) 어떤 함수 f가 필요하다.
이런 조건을 만족하여 감마 보정에 쓰이는 함수는 의외로 단순하다. 그냥 지수함수이다.
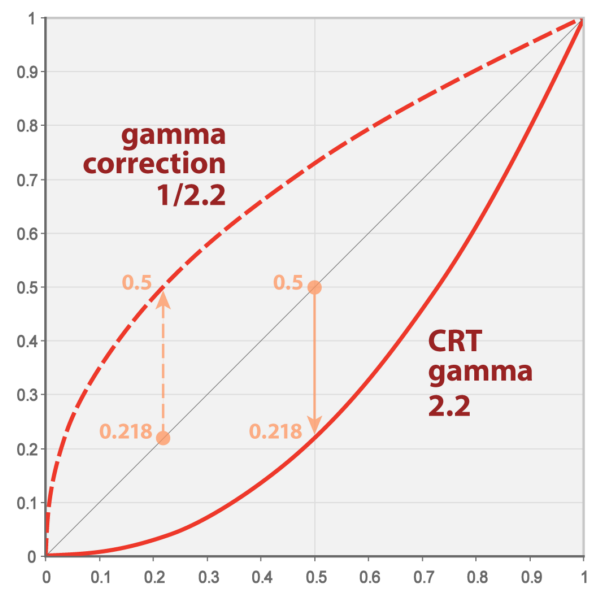
0보다 크고 1보다 작은 지수를 설정하면 구간 0~1에 대해서 f(x)는 x보다 값이 커진다. 그래서 원본보다 화면을 더 밝게 만드는 효과를 낸다. x=1에 근접할수록 그 증가폭이 작아질 것이다.
한편, 단순히 f(x) = x^t 말고.. f(x) = (1 - (1-x)^(1/t) )^t 는 어떨까 싶다.
얘는 t가 1/2일 때는 사분원의 궤적을 만들며, 2일 때는 2차 베지어 곡선을 만드니 참 흥미롭다. 그 외의 값일 때도 0 부근에서의 증가치와 1 부근에서의 감소치가 일치하는 나름 대칭형 곡선을 형성한다는 점에서 단순 지수함수와는 차이가 있다.
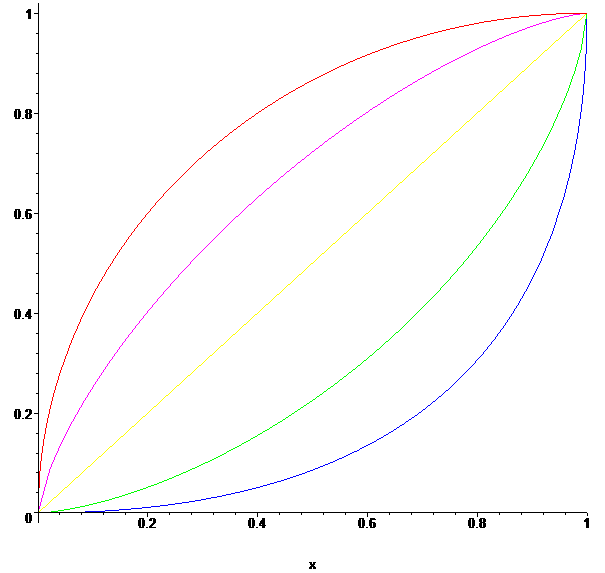
얘는 한눈에 봐도 적분하기 어렵게 생겼다. t가 치환적분이 가능한 1/2, 2 등의 알려진 값이 아니라 1/3 정도만 돼도 0부터 1까지의 면적, 다시 말해 정적분의 값은 초등함수의 형태로 표현되지 못한다.
2. 좌우대칭 종 모양
함수 중에는.. 값 자체는 전부 양수이지만 거의 전구간에서 0에 가깝고, f(-x)=f(x)인 우함수이고, 원점 x=0 주변에서만 최대값이 언덕처럼 봉긋 솟아 있는 물건이 있다.
이런 함수의 대표적인 예는 바로.. 확률· 통계의 영원한 친구인 정규 분포 확률 밀도 함수이다.
얘의 본질은 상수의 -x^2승이다. 그냥 지수가 아니라 음의 제곱 지수이다.
이런 함수도 부정적분이 깔끔한 형태로 나오지 않으며, 일부 구간의 정적분을 구하려면 수치해석을 동원해야 한다.
그 대신 얘는 음의 무한대에서 양의 무한대까지 함수 전체를 적분한 면적을 구할 수 있다. 가령, e^(-x^2)의 전체 정적분은 sqrt(Pi), 즉 원주율의 제곱근이다. (약 1.7724..)
전구간의 적분 면적은 옛날에 독일의 그 가우스라는 수학자가 이 종 모양을 입체 공간에서 뺑 돌려서 회전체의 부피를 구하는 식으로 발상을 전환하여 구했다. 일종의 이상 적분 기법인데, 더 이상의 자세한 설명은 생략한다. 고등학교 수준에서는 이 함수의 해석학적 특성을 도저히 따져볼 수 없다.
평균 0, 표준편차 1의 표준 정규 분포의 확률 밀도 함수는 저 함수에서 지수를 -x^2 / 2로 절반으로 나누고, 함수값에다가 1/sqrt(2*Pi)도 곱해서 전구간의 면적이 1이 되게 한 형태이다.
그럼 정규분포 함수보다 해석학적으로 분석하기 더 쉬운(?) 함수 중에는 좌우대칭 종 모양이 없을까?
바로 삼각학수 '탄젠트'의 '변종'에 속하는 놈들의 '도함수'가 이 범주에 든다.
탄젠트의 역함수인 arctan(x)는 도함수가 1/(x^2+1)이라는 꽤 단순한 형태인데, 그래프는 종 모양이다. x=0에서 최대값이 1이고, 전체 면적은 pi이다.
그리고 하이퍼볼릭 탄젠트 tanh(x)는 도함수가 1-tanh(x)^2로 기묘하게 구해지는데, 얘 역시 x=0에서 최대값이 1이면서 전체 면적은 2이다.
숫자 공부를 손 놓은지 10수 년이 지나서 그런지 이런 기본 기초 하나도 갑자기 새삼스럽게 느껴진다.
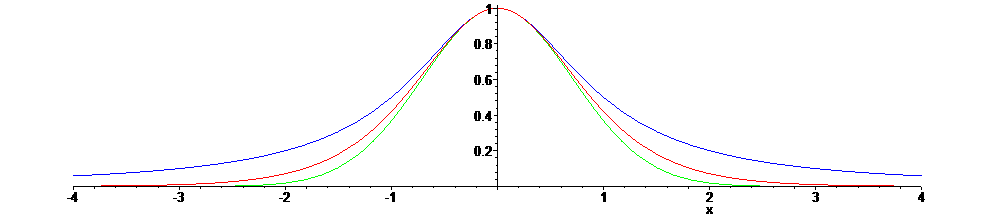
얘들은 그 정의상 자신의 부정적분이 깔끔하게 존재한다.
부정적분에 속하는 arctan이나 tanh이라는 오리지널 함수를 살펴보면.. 단조증가이면서 f(x)=-f(-x)인 기함수이며, 무한대로 갈수록 특정값에 수렴하고 반대로 무한소로 갈수록 음의 특정값에 수렴하는 걸 알 수 있다. 함수의 기울기는 x=0일 때 가장 크다.
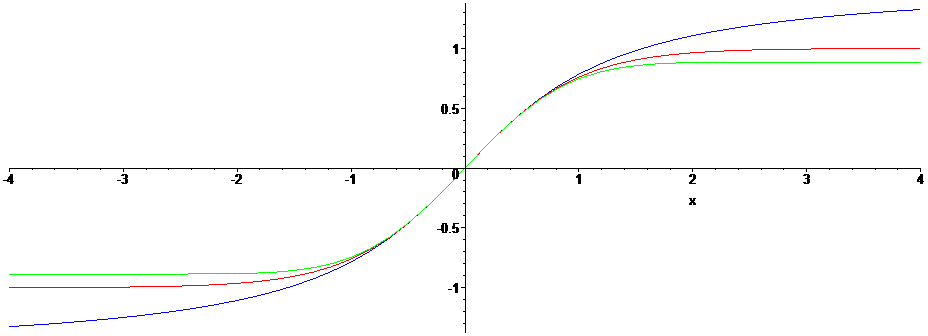
요런 모양의 함수만을 일컫는 용어가 "sigmoid"라고 있다. 선형이 얼추 기울어진 S자 모양이라는 점에서 유래된 명칭이다.
특히 tanh의 경우 sigmoid 함수의 대표격으로 여겨지며, Logistic function이라는 이름으로 배율 변경과 평행이동만 된 바리에이션이 쓰이기도 한다.
맨 먼저 다뤘던 확률 밀도 함수를 0부터 x까지 정적분한 함수는 수학에서 따로 '오차 함수'라고 불리며 중요하게 다뤄진다. 5차가 아니라 error라는 뜻이다. 얘도 물론 sigmoid에 속한다.
그렇잖아도 5차 이상의 방정식은 유한 번의 사칙과 거듭제곱으로 표현할 수 없는 근을 가질 수 있는데, 적분은 마치 그런 것처럼 x^x, sin(x)/x, 1/ln(x)처럼 단순한 식조차도 초등함수의 형태로 표현되지 않는 결과가 나올 수 있고 미분보다 어려운 연산으로 간주되는 걸까? 하긴, 1/x의 부정적분이 갑자기 ln(x)가 나오는 것에서부터 적분의 난해함이 발현되는 것인지도 모르겠다.
아무튼..
직선을 굽게 하는 1번 모양, 종처럼 생긴 2번 모양, 그리고 2번을 적분한 S자 모양까지..
요런 함수가 있다는 걸 알아 두면 코딩 하다가 언젠가 써먹을 날이 올 수도 있을 것이다.
Posted by 사무엘


