다음은 고등학교 수준에서 다뤄졌을 법한 전형적인 확률· 조합 문제이다.
수가 커질수록 소수를 발견하기 어려워지는 것만큼이나 저 확률은 0으로 수렴이라도 하는 걸까? 답부터 말하자면 그렇지 않다. N이 커질수록 그 확률은 1/e 에 수렴한다.
즉, 대략 37% 정도 된다는 뜻이고 이는 3지선다 문제를 깬또-_-로 맞힐 확률과 고만고만함을 의미한다. (깬또는 도대체 어느 나라 어원의 말일까? 순우리말이라면 흠좀무) 하필 자연대수와 관계가 있는 확률로 수렴한다는 것도 흥미로운 점.
신기하지 않은가? 이 정도면 여러분이 감으로 예상한 확률보다 높은 걸까 낮은 걸까? 수학이 좋은 점은, 인간의 감만으로는 아리까리한 문제에 대해서 명확하게 이렇게 될 수밖에 없다는 답을 제시한다는 것이다. 영적인 안목만 없을 뿐이지 추상적인 세계에서는 성경만큼이나 100% 절대무오한 진리를 담고 있는 학문이 바로 수학이다.
N개의 모자를 늘어놓을 수 있는 모든 가짓수는 잘 알다시피 N! (팩토리얼)이다.
N=2인 경우라면 1 2가 2 1로 뒤바뀌는 경우밖에 없으므로 1/2 = 50%
N=3이면 6가지 조합 중에 2 3 1, 3 1 2가 존재하므로 2/6 ≒ 33.3%
N=4는 잘 세어 보면 9가지 경우가 존재하여 9/24 = 37.5%
N=5일 때는 44가지 경우가 있다. 44/120 ≒ 36.7%
그리고 쭉쭉쭉...;;
그런데 이 가짓수에서 재미있는 패턴이 발견된다.
가짓수를 나타내는 함수를 f(x)라고 정의하면, 일단 f(x)의 값은 x-1의 배수임이 반드시 보장된다.
f(5)는 4의 배수인 11, f(4)는 3의 배수인 9인 식이다.
실제로 가짓수를 세어 보면, 왜 그렇게 되는지 알 수 있다.
이 f(x)를 구하는 방법은 점화식으로 의외로 간단하게 유도된다.
패턴을 잘 관찰해 보면 f(1)=0, f(2)=1 이후로 f(x) = (x-1)*(f(x-1)+f(x-2))가 된다.
f(4) = 3*(1+2) = 9
f(5) = 4*(2+9) = 44
f(6) = 5*(9+44) = 265
숫자의 증가의 폭이 팩토리얼과 동급으로 폭발적인 건 마찬가지이기 때문에, 그 비율의 극한이 0이나 무한대가 아니라 상수로 나온다.
f(x) = f(x-1)+f(x-2)인 피보나치 수열 점화식에다가 (x-1)을 곱한 것밖에 없으나, 점화식의 특성상 그 여파는 쌓이고 쌓이면서 훨씬 더 커진다. 피보나치 수열의 일반항은 2^n 같은 지수함수급인 반면 저건 팩토리얼급..;; 팩토리얼 자체가 f(x) = x*f(x-1)로, 점화식에 덧셈도 모자라서 곱셈이 등장하니까 말이다.
본인은 1/e라고 하면 x^x 함수를 최소로 만드는 값이기도 하다는 것을 예전부터 알고 있었다.
x^x는 a^x 같은 지수함수는 말할 것도 없고 심지어 팩토리얼보다도 더욱 폭발적으로 증가하는 괴랄한 함수이다.
이 함수는 양변에 로그를 씌워서 미분하는데, 도함수는 x^x * (ln x + 1)이 된다.
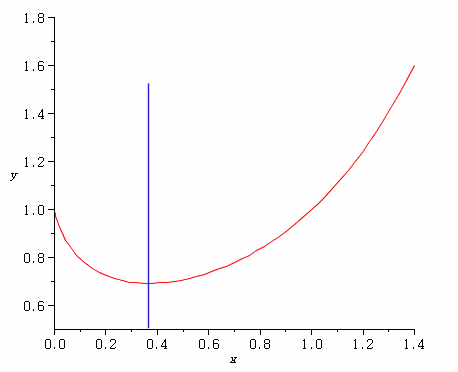
양수 x에 대해서 x^x 자체는 0이 결코 될 수가 없다(x가 0에 가까워져도 함수값은 1에 수렴). 하지만 x에다 1/e를 집어넣으면 ln x + 1이 ln 1 - ln e + 1 = 0-1+1 = 0이 된다. 고로 도함수의 값은 0. 이때가 최소이며, 그 최소값은 e^(-1/e)에 해당하는 약 0.69 정도.
e 자체뿐만이 아니라 e의 역수도 이런 의미를 지닌다는 걸 알 수 있다. 아래 그림을 참고하라.
대표적인 공돌이 유머인 미분 귀신 적분 귀신에 잘 묘사되어 있듯, 다항함수는 유한 번 미분하면 0이 되어 버린다. 그러나 초월함수들은 미분을 거듭해도 전혀 줄어들지 않으며 오히려 쓸데없는 계수들이 덧붙거나(지수함수), 형태만 바꾸면서 뱅글뱅글 순환한다(삼각함수).
그런데 그 정점에 있는 것이 바로 e^x이다. 미분해도 적분해도 형태가 전혀 변하지 않는다. ^^;;;
이 녀석은 테일러 급수로 다항식 전개를 해 보면.. 진짜 그렇게 될 수밖에 없는 형태임을 알 수 있다.
테일러 급수 자체가, 특정 지점에서 주어진 함수와 함수값과 n차까지 도함수가 일치하는 다항함수를 구하는 것이니 원..
1 + x + x^2/2 + x^3/6 + x^4/4! + x^5/5! ....
이게 끝없이 반복되니까 미분하면 왼쪽으로 shift, 적분하면 오른쪽으로 shift.. -_-;;
x에다가 1을 집어넣으면 결국 자연대수 e는 1부터 시작해 팩토리얼들의 역수의 합으로 2.71828...로 시작하는 그 값이 자연스럽게 유도된다. 수학에서 원주율 다음으로 유명하고 중요한 상수이다.
2.718281828 ..1828이 잠시 반복되는 덕분에 파이보다 외우기 쉽다.
우리는 학교 수학 시간에 자연상수에 대해서 (1+ 1/n)^n의 n 무한대 극한값이라고 처음으로 배운다. 이게 e로 수렴한다는 것도 무척 재미있는 사실이긴 하나, 저 식은 수렴 속도가 매우 느려서 비실용적이다. n=1000이 돼도 아직 2.716이고 2.718에도 도달 안 해 있다.
그 반면 팩토리얼 역수의 합은 직관적이고 수렴 속도도 꽤 빠른 편이어서 좋다. 6!까지 갈 때 이미 2.718에 도달하고 9!에서 벌써 소숫점 여섯째 자리까지 일치하기 시작한다. 굿..;;
범위가 0부터 1까지인 n차원 공간상의 점 P(a1, a2, a3, ... a_n)이 있을 때, 0<a1<a2<a3<...<a_n을 만족하는 영역이 차지하는 부피(?) 내지 product는 어떻게 될까? 1/n!이다. 2차원일 때는 한 변의 길이가 1인 삼각형의 넓이가 되므로 1/2, 3차원일 때는 삼각뿔의 부피가 되므로 거기에다가 1/3을 또 곱하면 1/6이 되고, 차원이 그보다 올라가도 적분을 거듭하면 그런 식으로 값이 더욱 작아진다는 걸 알 수 있다.
미분이나 적분을 하면 항의 차수가 1 늘거나 감소하는 대신에 원래 갖고 있던 계수가 곱해지거나 나눠지는 만큼, 이 과정을 일반화하면 팩토리얼 연산도 태생적으로 연관이 되지 않을 수 없게 되는 것 같다. 팩토리얼은 확률· 조합 같은 이산수학 영역뿐만이 아니라 해석학에서도 중요한 의미를 지니는 연산인 셈이다.
아울러, -1승이라 할 수 있는 1/x만 적분하면 ln x라는 완전히 다른 함수가 된다는 것도 아주 흥미로운 점이 아닐 수 없다.
Posted by 사무엘


