원점 O에서 시작하는 벡터 A, B가 있다. 그런데 A와 B가 형성하는 내각을 이등분하는 중앙을 지나는 벡터 C를 구하려면 어떡하면 좋을까? 각도를 결정하는 방향만 정확하게 나오면 되며, 길이가 어떻게 되는지는 신경 쓰지 않아도 된다.
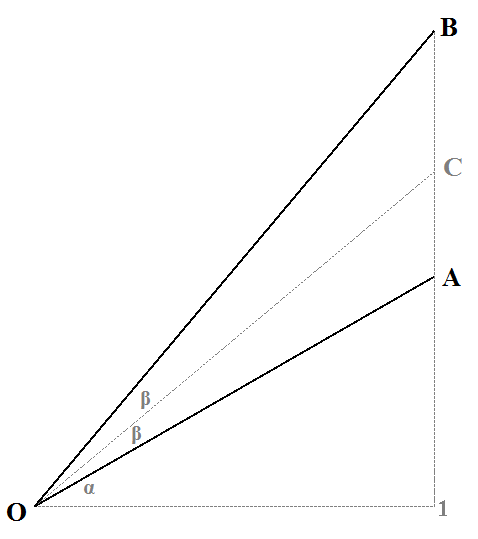
단순히 벡터 A와 B를 더하기만 해서는 내각을 정확하게 이등분할 수 없다는 것을 알 수 있다.
더하기만 해서 얻은 벡터는 삼각형 OAB의 '무게중심'을 지나게 된다.
그러나 내각을 이등분하는 벡터는 삼각형 OAB의 '내심'을 지나게 해야 하기 때문이다.
이 문제는 의외로 어렵지 않다.
선분 AB의 위에 있는 점 C를 설정하되, 선분 OA: OB의 길이의 비와 선분 AC: BC의 길이의 비가 일치하는 지점 C를 찾으면 된다. 그러면 원점에서 시작하는 벡터 C가 바로 벡터 A와 B의 내각을 이등분하는 벡터가 된다.
그렇게 되는 이유를 해석학적으로 따져 보면 다음과 같다.
위의 그림에서 점 A의 좌표는 (1, tan α)이고 B의 좌표는 (1, tan(α+2β) )이다.
그리고 선분 OA의 길이는 피타고라스의 정리에 따라 sqrt(1 + (tan α)^2)이요, 선분 OB의 길이는 더 복잡한 sqrt(1 + (tan (α+2β))^2)가 되는데..
이 둘의 비율이 AC와 BC의 길이의 비와 같다는 뜻이다. AC와 BC는 각각 (tan α+β - tan α), (tan α+2β - tan α+β)로 표현될 것이다.
한쪽은 탄젠트값의 제곱에다가 제곱근이 나오고, 다른 한쪽은 제곱 연산은 없지만 서로 다른 탄젠트 함수의 뺄셈이 나온다. 언뜻 보기에 둘은 서로 비슷한 구석을 찾을 수 없다. 그렇다면 이들이 비율이 서로 일치한다는 걸 어떻게 보일 수 있을까?
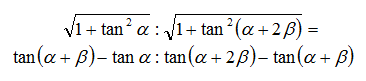
여기서 탄젠트 제곱과 제곱근을 쉽게 정리하는 방법이 있다. tan x = sin x / cos x이므로, 1을 분모와 분자가 모두 cos^2 x 인 분수로 간주하여 1 + tan^2 x는 (cos^2 x + sin^2 x)/cos^2 x라고 볼 수 있다.
그럼 분자는 얼씨구나 1로 약분된다. 근호 안에는 1/cos^2 x밖에 남지 않으니, 전체 식은 단순히 1/cos x로 줄어든다.
비례식에서 내항과 외항의 곱은 같아야 하므로, 내항의 곱을 분자에, 외항의 곱을 분모에다 얹은 분수를 설정해 보겠다. 이 수의 값이 1이면 목적이 달성되는 것이므로 어느 걸 분자에, 어느 걸 분모에 얹을지는 그리 중요하지 않다.
식에서는 α+2β, α+β, α라는 세 종류의 각이 쓰이는데, 일단 시각적인 혼동을 줄이기 위해서 앞의 두 아이템을 이제부터는 각각 A, B라는 매크로로 치환하였다.
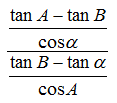
이제 예전보다 문제가 꽤 단순해졌다.
분자와 분모가 또 분수로 구성되어 있는데, 이것을 통분하는 방법은 간단하다. 분자와 분모에 모두 똑같이 cos A cos B cos α를 한꺼번에 곱해 주면 된다.
그러면 각 분자와 분모에 이중으로 분모로 남아 있던 cos α나 cos A는 약분되어 없어지고, tan 함수도 내부적으로 갖고 있던 cos 나눗셈이 약분되면서 sin으로 바뀐다. 그리고 약분되지 않은 변수에 속하는 cos만이 남는다.
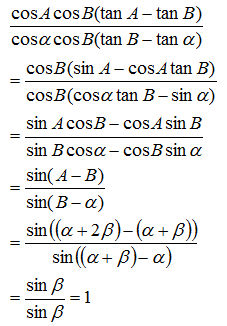
그 뒤의 절차는 일사천리이다.
sin 함수와 cos 함수의 곱이 규칙적인 패턴으로 남는데, 이것은 딱 정확하게 sin(x-y) 꼴로 정리가 된다.
그리고 이제야 매크로 A, B를 원래의 각으로 전개해 보면, A-B와 B-α의 각은 애초에 같은 값이었다는 것을 알 수 있다. 따라서 분자와 분모는 동치이고 원래의 비례식도 항등식으로서 성립한다는 게 밝혀진다.
뭔가 당연한 사실을 필요 이상으로 너무 복잡하게 파헤친 거라는 느낌이 든다. =_=
삼각함수, 벡터 이런 쪽은 컴퓨터에서 기하를 다루는 데 없어서는 안 될 마법과 같은 도구임이 분명하다.
Posted by 사무엘


