김 용묵의 절대공간 - 블로그

지금 와서 가만히 생각해 보니, 컴퓨터 알고리즘을 동원하여 푸는 문제들은 다음과 같은 세 범주로 나눌 수 있는 것 같다. 뒤로 갈수록 설명이 길어진다.

1. 최적해를 다항 시간 만에 구할 수 있으며, 직관적인 brute-force 알고리즘과 뭔가 머리를 쓴 알고리즘이 시간 복잡도 면에서 충분히 유의미한 차이를 보이는 문제

간단한 발상의 전환으로 인해서 속도가 드라마틱하게 빨라질 수 있고, 알고리즘에 대한 정량적인 분석도 어렵지 않게 다 되는 경우이다. 요런 게 알고리즘 중에서는 가장 무난하다. 정보 올림피아드에도 이런 부류가 가장 많이 나온다.
가장 전형적인 예는 시간 복잡도 O(n^2)가 O(n log n)으로 바뀐다거나, 지수함수 복잡도가 O(n^2)로, 혹은 O(n^3)이 O(n^2)로 바뀌는 것이다. 물론 시간 복잡도를 줄이기 위해서는 공간 복잡도가 시공간 trade-off 차원에서 추가되는 경우가 대부분이다. 중간 계산 결과들을 모두 저장해 놓는 다이나믹 프로그래밍 문제가 대표적인 예이다.

정렬, common subsequence 구하기, 그래프에서 최단거리 찾기 같은 깔끔하고 고전적인 문제들이 많다. 기하 분야로 가면 convex hull 구하기, 거리가 가까운 두 점 구하기도 있다. 하지만 세상에 산적한 문제들 중에는 이 1번 부류에 속하지 않는 것도 많다.

2. 최적해를 다항 시간 만에 구하는 것이 가능하지 않은 (것으로 여겨지는) 문제

P에는 속하지 않지만 NP에는 속하는 급의 문제이다. 이건 다항 시간 만에 원천적으로 풀 수 없는 문제를 말하는 게 아니며 개념과 관점이 사뭇 다르다. 비결정성 튜링 기계라는, 실물이 없는 이론적인 계산 기계에서는 그래도 다항 시간 안에 풀 수 있다는 뜻이다.

입력 데이터의 개수 n에 비례해서 상수의 n승 내지 n 팩토리얼 개수의 가짓수를 일일이 다 따져야 하는 문제라면 다항 시간 만에 풀 수가 없다. 그런데 실생활에는 이런 무지막지하게 어려운 문제가 은근히 많이 존재한다. 진짜 말 그대로 n!개짜리 뺑이를 쳐야 하는 외판원 문제가 대표적이고, 그래프에도 '해밀턴 경로 문제'처럼 이런 어려운 문제가 산적해 있다. 이런 분야의 문제는 소위 말하는 NP-complete, NP-hard이기도 하다.

요런 문제는 brute force 알고리즘으로는 대용량 데이터를 도저히 감당할 수 없고 그렇다고 다항 시간 최적해 알고리즘이 있는 것도 아니기 때문에, 이런 문제는 100% 최적해는 포기하고 그 대신 95+n%짜리로 절충하고 시간 복잡도는 O(n^2)로.. 뭔가 손실 압축스럽게 tradeoff를 하게 된다.
국제 정보 올림피아드에는 이런 문제가 많이는 안 나오지만 전혀 안 나오는 건 아니다. 출제된다면 답은 최적해와의 비율로 점수가 매겨지며, 프로그램 실행이 아닌 그냥 제출형으로 출제되기도 한다.

P와 NP 사이의 관계는 전산학계에서 만년 떡밥이다. 현실에서는 마치 장기간 실종자를 법적으로 사망한 것과 마찬가지로 간주하듯이 P와 NP는 서로 같지 않다고 여겨지고 있다. 이를 전제로 깔고 발표된 연구 논문들도 수두룩하다. 하지만 그게 정말로 딱 그러한지는 전세계의 날고 기는 수학자들이 여전히 완벽하게 규명을 못 하고 있다.

엔하위키에는 P!=NP임을 증명하는 사람은 전산학 전공 서적에 이름이 실릴 것이고, P=NP임을 증명하는 사람은 아예 초등학생 위인전에 등재될 것이라고 얘기를 했는데... 적절한 비유인 것 같다. 지수함수 brute force 말고는 답이 없는 문제가 좀 있어야 암호와 보안 업계도 먹고 살 수 있을 텐데..!

3. 최적해를 다항 시간 만에 구할 수 있음이 명백하고, naive 알고리즘도 실생활에서 그럭저럭 나쁘지 않은 결과가 나오지만, 그래도 미시적· 이론적으로는 최적화 여지가 더 있는 심오한 문제

말을 이렇게 어렵게만 써 놓으면 실감이 잘 안 가지만 이 그룹에 속하는 문제의 예를 보면 곧장 "아~!" 소리가 나올 것이다. 이 분야에도 어려운 문제들이 은근히 많다.

(1) 문자열 검색
실생활에서는 그냥 단순한 알고리즘이 장땡이다. 원본 문자열을 한 글자씩 훑으면서 그 글자부터 시작하면 대상 문자열과 일치하는지 처음부터 일일이 비교한다. 실생활에서 텍스트 에디터는 대소문자 무시, 온전한 단어 같은 복잡한 옵션들이 존재하며 각 글자들의 변별성도 높다(대상 문자열과 일치하지 않는 경우 첫 한두/두세 글자에서 곧바로 mismatch가 발생해서 걸러진다는 뜻). 그 때문에 그냥 이렇게만 해도 딱히 비효율이 발생할 일이 없다.

하지만 문자열 검색이라는 건 실무가 아닌 이론으로 들어가면 생각보다 굉장히 심오하고 난해한 분야이다. 원본과 대상 문자열이 자연어 텍스트가 아니라 오로지 0과 1로만 이뤄진 엄청 길고 빽빽하고 아무 치우침이 없는 엔트로피 최강의 난수 비트라고 생각하자. 그러면 예전에 패턴이 어디서부터 어긋났는지를 전혀 감안하지 않은 채 오로지 1글자씩만 전진하는 방식은 효율이 상당히 떨어진다. 이제야 좀 더 똑똑한 문자열 검색 알고리즘이 필요해진다.

퀵 정렬의 중간값(pivot) 선택 알고리즘을 의도적으로 엿먹이는 '안티' 데이터 생성 알고리즘만큼이나..
특정 문자열 검색 알고리즘을 엿먹여서 언제나 최악의 경우로 한 글자씩만 전진하게 만드는 문자열 데이터를 생성하는 안티 알고리즘도 있을 것이다.

(2) 팬케이크 정렬
a1부터 a_n까지 임의의 수 배열이 존재하는데, 우리가 이 수열에 대해 취할 수 있는 동작은 여느 정렬 알고리즘처럼 임의의 두 원소끼리의 교환이 아니다. 1~2, 1~3 또는 1..m (m<=n)처럼 첫째부터 m째의 원소들을 모조리 역순으로 뒤집는 것만 가능하다. 1 7 4 2였으면 2 4 7 1로 바꾼다는 것. n개의 임의의 수열이 있을 때 수열을 정렬하기 위해 필요한 이론적인 최대 뒤집기 횟수는 정확하게 얼마나 될까? 한꺼번에 몇 개를 뒤집건 한번 뒤집는 데 걸리는 시간은 무조건 상수라고 가정하고, 뒤집기 자체 외에 다른 계산의 비용(가령, 현 구간에서 maximum 값을 찾는 것)은 전혀 고려하지 않아도 된다.

본인은 아주 어렸을 때 GWBASIC 교재에서 이 팬케이크 정렬 문제와 같은 방식으로 수열을 뒤집어서 "사람으로 하여금 문제를 풀게 하는" 프로그램을 본 기억이 있다. 프로그램의 이름이 REVERSE였다.
이 문제는 마치 선택 정렬과 비슷한 방식으로 명백한 해법이 존재한다. 가장 큰 수가 m째 원소에 존재한다면 m만치 뒤집어서 가장 큰 수가 맨 처음에 오게 한 뒤, 판 전체를 뒤집어서(n만치) 그 수가 맨 뒤로 가게 하면 된다. 이 과정을 그 다음 둘째, 셋째로 큰 수에 대해서 계속 적용하면 된다.

그렇게 명백한 해법의 계산 횟수는 최대 2*n-3으로 알려져 있다. 하지만 이것은 그렇게 뒤집은 여파가 다음으로 큰 수들을 정렬하는 데 끼치는 영향이 감안되어 있지 않다. 물론 여기서 좀더 머리를 써 봤자 2n이던 계수가 1.xx 정도로나 바뀌지 그게 n 내지 심지어 log n급으로 확 바뀌지는 못한다. 비록 O(n) 표기상으로는 동일하지만 그렇게 상수 계수를 조금이라도 줄이는 최적화이다 보니, 알고리즘이 더 까다롭고 머리가 아프다.

마이크로소프트의 창립자인 그 빌 게이츠가 1979년에 바로 이 문제의 계산 횟수를 최적화하는 알고리즘을 (공동) 연구하여 이산수학 학술지에다 투고했었다. 이 사람의 기록은 그로부터 거의 30년이 지난 2008년에야 더 정교한 알고리즘이 나옴으로써 깨졌다. 이것은 빌이 단순히 비즈니스맨이기만 한 게 아니라 엔지니어 기질도 얼마나 뛰어났고 수학 쪽으로도 얼마나 천재였는지를 짐작케 하는 대목이다. 학부 중퇴 학력만으로도 이미 전산학 석· 박사급의 걸출한 리서치를 했으니 말이다.

(3) 행렬의 곱셈
갑자기 팬케이크 정렬 얘기가 좀 길어졌는데 다음 항목으로 넘어가자면.. 계산 관련 알고리즘도 이런 급에 속한다. 대표적으로 행렬.

일반적으로야 두 개의 n*n 정방행렬끼리 곱셈을 하는 데 필요한 계산량, 정확히 말해 두 수 사이의 곱셈 횟수는 정확하게 O(n^3)에 비례해서 증가한다. 그러나 거대한 행렬을 2*2 형태의 네 개로 쪼개고, 덧셈을 늘리는 대신 곱셈을 줄이는 방식으로 최적화를 하는 게 가능하다. 게다가 쪼개진 행렬이 여전히 크다면 그걸 또 재귀적으로 쪼갤 수 있다.
a+bi와 c+di라는 복소수의 곱셈을 위해서 통상적으로는 ab, ac, bc, bd라고 곱셈이 총 4회 필요하다고 여겨지지만 실은 덧셈을 더 하는 대신에 곱셈은 ac, bd와 (a+b)*(c+d)로 3회로 줄일 수 있지 않은가? 그런 식으로 줄인 것이다.

그렇게 해서 O(n^3)보다 이론상 작은 시간 복잡도가 최초로 제안된 게 1969년에 나온 슈트라센 알고리즘이다. 대략 O(n^2.8). 정확하게 2.8인 건 아니고 지수 자체가 로그 n 이런 형태로 떨어진다. 프랙탈의 차원 수가 로그로 표현되는 것처럼 말이다.
여기서 2.8x의 정확한 의미는 log[2] 7이다. 원래 2*2 행렬 두 개를 곱하기 위해서는 상수 곱셈이 8회 필요한데, 중간 과정의 공식들을 궁극의 캐사기 테크닉을 동원하여 변형했다. 어마어마한 양의 우회 연산을 통해 덧셈은 횟수가 왕창 늘었지만 곱셈이 8회에서 7회로 딱 1회 줄었다! (도대체 무슨 약 빨고 연구해서 이런 걸 생각해 냈을까? ㄷㄷ) 이 여파가 분할 정복법의 특성상 재귀· 연쇄적으로 적용된 덕분에 전체 시간 복잡도가 감소한 것이다.

그리고 이 바닥도 발전에 발전을 거듭한 덕분에 오늘날은 무려 O(n^2.4)대까지 곤두박질쳤다. 덧셈과는 달리 곱셈은 이런 최적화의 여지가 존재한다는 사실 자체가 아주 신기하지 않은가? 크기가 서로 다른 행렬들의 최소 곱셈 횟수를 구하는 다이나믹 프로그래밍 문제하고는 완전 별개의 영역이다.

아래의 그림을 보자(움짤임). RGB라는 세 대의 차량이 서로 부딪치지 않고 G는 그대로 위로, R과 B는 서로 좌우가 엇갈리게 빠져나가려면 어떻게 하면 좋을까? 아래의 중앙은 길이 막혔기 때문에 횡단을 할 수 없다.
결국 가운데 G는 곧이곧대로 위로 나가서는 안 되며, R과 B의 경로를 피해서 몇 배나 더 긴 우회를 해야 한다. 하지만 그래도 RGB 모두 신호 대기가 없이 서로 엇갈리는 방향으로 술술 소통이 가능하다.

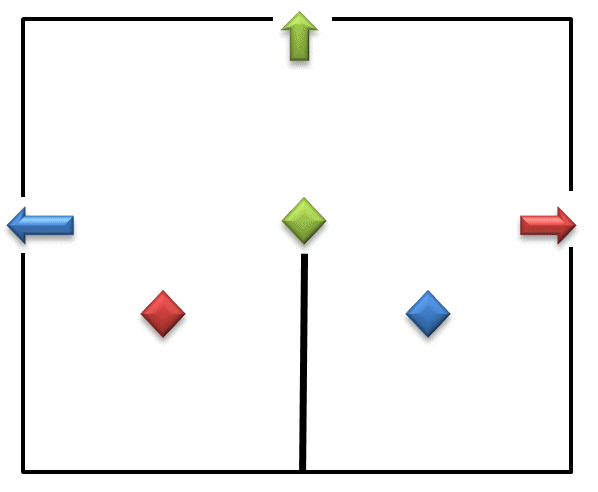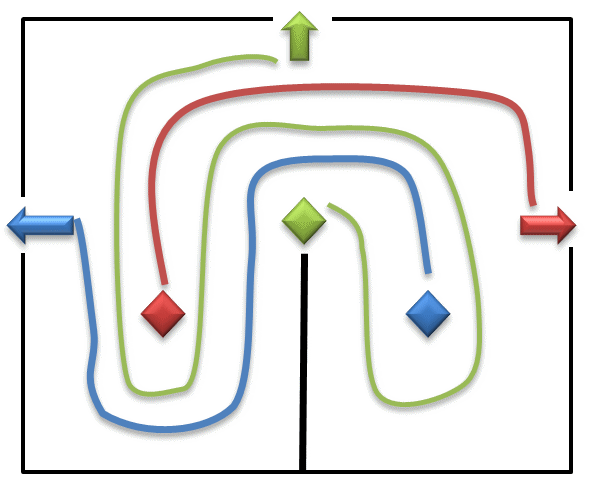
자연에는 관성이라는 게 존재하니, 다리가 아니라 바퀴가 달린 자동차나 열차에게는 우회를 하더라도 이게 훨씬 더 나은 방법인 것이다.
행렬도 덧셈이라는 우회가 아무리 몇 배로 더 늘어 봤자, 아주 큰 행렬(차량 소통이 엄청 많을 때)에 대해서는 곱셈이 눈꼽만치라도 줄어드는 게 도로로 치면 신호 대기가 없어지는 것에 맞먹는 이익이 될 수 있다는 생각이 든다.

물론 행렬의 곱셈 시간 복잡도가 O(n^2)보다 더 낮아질 리는 없으며, 저런 알고리즘들은 지수를 줄이는 대신 공간 복잡도(스택 사용..) 같은 다른 오버헤드가 왕창 커졌다는 점을 감안해야 한다. 크기가 몇십~몇백 정도 되는 초대형 행렬에서 두각을 발휘하지, 그냥 3차원 그래픽용으로나 간단히 쓰이는 3*3이나 끽해야 4*4 행렬에서 적용할 만하지는 않다.

Posted by 사무엘

메리 크리스마스 인사부터 하고... ㅋ
본인 블로그의 정기 구독자-_-라면 이미 귀가 따갑게 들으셨겠지만, 본인은 10년 전, 제 17회 한국 정보 올림피아드(KOI) 공모 부문의 고등부 대상 수상자이다. 그리고 얼마 전엔 모듈 음악에 대해 글을 쓰면서, 바로 전 해인 16회 대회의 고등부 금상 수상자에 대해서 언급했었다. 그때는 대상 수상자가 없었다.
이제 이 글에서는 전 회에 이어, 본인이 참가한 해의 바로 이듬해인 18회 대회의 고등부 대상 수상자에 대해서 얘기하도록 하겠다.

그 주인공은 바로 김 성진 씨.
학창 시절부터 일찌감치 경시가 아닌 공모 테크를 타고 뭔가 창의적인 아이템으로 소프트웨어 개발에 매진했다는 점에서는 본인의 진로와 비슷하다. 그리고 지금까지 한 우물만 죽어라고 파고 있다는 점에서도 본인과 공통점이 있다. (무슨 분야인지는 곧 소개하겠다.) 그런 외골수는 나밖에 없는 줄 알았는데 여기 또 있다. ^^

이 친구는 KOI뿐만이 아니라 창의성 대회나 다른 소프트웨어 공모전 등에서 자기의 동일 아이템으로 상을 휩쓸었고, 본인보다 매스컴도 훨씬 더 많이 탔으며 IT 분야 사회 활동을 더 활발히 해 왔다. 사교/사회성, 정치성 자체가 본인과는 비교할 수 없이 더 뛰어난 사람이다.

이 친구의 보유 기술 및 아이템이 뭐냐 하면,
인터넷 보안, 음란 사이트 차단, 자녀 컴퓨터 사용 제어(parental control), 인터넷/게임 중독 예방 쪽이다. 관심 분야부터가 지극히 사회적인 쪽이지 않은가?
그걸 수 년째 연구한 솔루션을 만들어서 그는 18회 KOI에서 당당히 대상을 차지하고, 일반고 출신으로서 지정 대회 우수 입상자로 카이스트에 진학했다. 본인은 그와 2001년에 처음으로 메신저에서 만났고, 이내 학교에서 볼 수 있었다. 굉장히 예의바르고 인상이 좋은 사람이었다는 기억은 아직까지 생생하다.

그 후 2004년 가을에는 전산학과에서 제 1회 KAIST Computing Festival이라는 행사를 열었는데, 그때 대회 참가자로서 또 서로 만날 일이 있었다.
그는 확실히 이론보다는 실무형 인재였고, 내 예상과는 달리 전산학과가 아닌 산업디자인과에 진학해 있었다. 전산/산디 복수 내지 부전공인지는 확실히 잘 모르겠다. 저런 친구야말로 카이스트 전산과의 학부 과목인 ‘컴윤리’는 꼭 들어야 했을 텐데 말이다. (그러고 보니 김 진형 교수님도 불과 몇 년 뒤면 정년이다. 세월 한번 무섭다.)

그는 산디과 소속답게 자기 작품을 소개하는 발표용 프레젠테이션은 정말 기가 막히게 잘 만들었던 걸로 본인의 기억에 남아 있다. HCI(사람-기계 커뮤니케이션) 쪽에도 관심이 많은 듯. 스티브 잡스 근성이라도 있는 걸까? ㄲㄲㄲ

뭐, 사족을 덧붙이자면 그 교내 공모전에서도 본인이 출품한 <날개셋> 한글 입력기 3.02가 1등을 했다.
카이스트 전산학과는 가히 전국에서 날고 기는 수학 덕후· 컴퓨터 괴물들이 우글거리는 곳이고, 난 그 집단 안에서는 별 보잘것없는 중하위권 학부생에 불과했다. 그럼에도 불구하고 거기서까지 내 작품이 최고로 인정받을 수 있었던 것은 1, 2년 연구한 작품이 아니니 짬과 연륜면에서 타 작품들과 비교가 안 되고, 또 한글을 이런 식으로 입력할 수 있다는 게 세벌식 사고방식으로는 당연한 것이지만 두벌식밖에 안 써 본 사람이라면 카이스트 교수에게라도 충분히 창의적이고 참신하게 작용했기 때문인 것 같다.

본인이 국어학하고 양다리를 걸쳤다면, 김 성진 씨는 디자인과 양다리를 걸쳤다. 그는 카이스트에서 산디과 석사까지 마친 후, 아예 (주)휴모션이라고 벤처기업 창업을 했다. 그게 2008년의 일이고, 현재까지 어엿한 사장님이 돼 있다. ^^;; 창업 과정에서 카이스트로부터 지원을 당연히 아주 많이 받았다. 보아하니 회사는 대전의 유성 고속버스 터미널에서 꽤 가까운 곳에 있는 듯.
사장이 디자인 전공이다 보니, 핵심 기술인 ‘컴퓨팅 안전’ 분야 솔루션뿐만이 아니라 웹사이트 내지 심지어 회사 CI의 디자인 용역까지 담당하는 모양이다. 대단한 후배이다. 본인과 나이 차차도 별로 안 난다.

정올 공모 출품작 아이템을 이렇게 사업 아이템으로까지 스스로 발전시켜 잘 나가고 있는 입상자가 주변에 있으니 부럽기도 하고 훈훈하다. 정올 공모에서 이렇게 입상하고 덤으로 카이스트 같은 좋은 면학 환경까지 거쳐 간 인재들이 특별히 전산학하고 다른 분야와의 학제간 연구를 통해 우리나라에 뭔가 좋은 일을 많이 했으면 좋겠다. 본인 역시 그 꿈을 이루려는 의욕이 있어서 뒤늦게나마 협동과정 대학원에 갔다. 나는 그렇게 학구파는 아니지만 저 친구 같은 사교력이나 사업 수완은 더 없기 때문에-_-;; 일단 공부부터 좀 하려고..;;
성진 후배가 이 글을 볼 일이 있을지 모르겠지만, 그의 성공과 사업의 번창을 기원한다.

Posted by 사무엘

오랜만에 알고리즘 얘기.
정보 올림피아드 공부를 한 적이 있는 분이라면, 제목에 등장한 용어가 아주 친숙할 것이다. 앞으로 LIS라고 줄여 일컫겠다.

어떤 수열이 왼쪽에서 오른쪽으로 나열돼 있으면, 그 배열 순서를 유지하면서 크기가 점진적으로 커지는 가장 긴 부분수열을 추출하는 것이 목표이다.
가령, {3, 2, 1, 4, 5, 2, 3, 5, 3, 6, 4} 같은 수열이 있으면
1, 2, 3, 5, 6이 가장 긴 solution이 된다. {3, 2, 1, 4, 5, 2, 3, 5, 3, 6,  4} OK?
정렬만큼이나 알고리즘 기초를 다지는 데 도움이 되는 흥미로운 문제이다.

이 문제는 간단하게 생각하면 다이나믹 프로그래밍(동적 계획법)을 적용한 O(n^2)의 시간 복잡도로 풀 수 있다. 작은 set에 대한 답을 구한 뒤 그 결과를 저장해 놓고, 그 set의 크기를 차츰 키우면서 작은 solution들을 종합하여 최종 solution을 구하는 방식.

매 원소에 대해서 자기까지 왔을 때 존재 가능한 subsequence의 최대 길이와, 그 subsequence 상에서 자기 앞 원소의 위치를 적어 놓는다. 그러면 다음 원소 차례가 됐을 때는 자기 앞 원소들을 일일이 탐색하여, 자기보다 값이 작으면서 잠재적 subsequence 길이가 최장으로 설정되어 있는 원소에다 자기를 연결해 놓는다. 물론 자기의 subsequence 길이는 1 증가시켜 놓고 말이다.

위와 같은 표가 완성되고 나면, 그 후 개수가 5로 가장 큰 9번 오프셋부터 시작하여 이전 참고 위치를 따라 역추적을 하면 LIS가 구해진다.

그런데 이걸 구하기 위해서 꼭 O(n^2)이나 되는 계산량이 필요할까? 더 효율적인 알고리즘은 없을까?
답은 ‘있다’이다. 물론 메모리 복잡도도 아까처럼 O(n)으로 완전히 동일하고 말이다.
이 새로운 알고리즘은 역시 길이가 n인 버퍼에다가 작업을 하는데, 버퍼의 용도가 아까와는 살짝 다르다.

이 버퍼 A[i](1<=i<=n)의 의미는, 길이가 i인 LIS를 구한다고 쳤을 때 존재 가능한 가장 작은 LIS 마지막 원소(와 그 원소의 위치)이다. 즉, 이 버퍼는 구해진 LIS의 길이만큼만 사용된다.

위의 예제 수열에서 매 원소가 들어올 때마다 버퍼는 다음과 같이 바뀌게 된다. 뒤에 새로운 원소가 추가되거나 이미 있는 값의 업데이트만 발생하지(O(1)), 배열 원소들을 전부 하나씩 밀어야 하는 삽입이나 삭제(O(n))가 발생하지는 않음을 염두에 두기 바란다.
3: 3
2: 2
1: 1
4: 1 4
5: 1 4 5
2: 1 2 5
3: 1 2 3
5: 1 2 3 5
3: 변화 없음
6: 1 2 3 5 6
4: 1 2 3 4 6

즉, 버퍼가 가리키고 있는 것은 각 길이별로 가장 작은 수일 뿐이다. 그러나 버퍼가 가리키는 순서대로 배열을 참조하면 수열이 언제나 오름차순, 즉 정렬이 돼 있다는 게 보장된다.
최소값을 갱신할 위치를 찾는 것은 이분 검색(binary search)으로 할 수 있다. 이 덕분에 작업이 O(n^2)에서 O(n log n)으로 줄어들 수 있게 된다. 정확하게 말하면 O(n log k)(k는 LIS 길이)이니 더욱 빠르다. worst case로 증가 수열을 만들 수가 없는 내림차순 수열을 던져 주면, 거의 O(n)이나 다름없는 속도로 금방 실행이 끝난다는 뜻이다.

물론, 이 버퍼에는 각 길이별로 가장 작은 증가 수열을 구하는 힌트만 들어있을 뿐, 가장 긴 LIS를 추적하는 정보는 전혀 들어있지 않다. 그렇기 때문에 추적 순서는 역시 별도의 배열에다 따로 보관해 놔야 하며 이 역시 그리 어렵지 않게 구현할 수 있다. 심심하신 분은 이 알고리즘을 직접 코딩해 보기 바란다.

정보 올림피아드를 공부하던 시절엔 이런 유형의 문제도 재미있었다. 뭐, 본인은 머리싸움에 쥐약인 타입인지라 경시 부문에서는 별 재미를 못 보고, 대박은 공모 부문에서 다 냈지만 말이다.

- 양수와 음수가 뒤섞인 n개의 수열이 있을 때 합이 가장 큰 구간을 O(n) 시간 만에 구하기
- 위와 비슷한 예로, 0.x와 n.x가 뒤섞인 n개의 수열이 있을 때 곱이 가장 큰 구간을 역시 O(n) 시간 만에 구하기
- x*y 2차원 배열이 있을 때, 이런 조건을 만족하는 가장 넓은 면적을 구하기 (1999년도 IOI의 공항 건설 부지 찾기 같은)

알고리즘이라는 게 OR(operations research)과 밀접한 관계가 있는 것 같다. 선형 계획법, 동적 계획법 같은 개념도 원래는 그 분야에서 유래되었기 때문에 용어에서 그다지 전산학적인 어원은 찾을 수 없다.
덧. algorithm인데 왜 다들 알고리듬이라고 적지 않고 알고리즘(=algorism?)이 보편화해 있는 걸까?

Posted by 사무엘

오늘의 얘깃거리는 컴퓨터와 음악이다. 이 두 분야와 관계가 있는 옛날 소프트웨어들에 대한 추억도 곁들어질 것이다. 쓰다 보니 글이 꽤 길어졌다. ㄲㄲ

여기서 음악 파일이란, 말 그대로 음표 정보를 기반으로 음악을 연주하는 데이터를 말한다. 과거의 컴퓨터는 어마어마한 양의 waveform 데이터를 실시간으로 읽어들여(심지어 압축을 풀면서) 재생하면서 게임까지 원활하게 돌릴 정도의 성능을 갖추지 못했다. 그렇기 때문에 이런 가벼운 음표 기반 음악 파일이 각광을 받았다. 이런 파일은 크기가 아주 작은 데다, 또 음악은 반복되는 멜로디나 리듬이 많다는 특성상 압축률도 높았다.

※ 애드립 ROL, IMS

일명 FM(주파수 변조 방식) 사운드이다.
sound.com, unsound.com, 그리고 CGA 640*200이라는 흠좀무스러운 그래픽 모드에서 실행되던 애드립 Visual Composer (무려 1987년도 프로그램이다!).
standard.bnk, 이야기, implay 이런 것들을 기억한다면 당신은 진정 old timer 인증이다.

피아노, 바이올린, 색소폰 같은 현실의 악기와 비교했을 때는 분명 모자란 게 있지만 이 FM 음악은 나름 자신만의 개성과 색깔이 있었다. 단적인 예로, 과거 <그 날이 오면 3>의 환상적인 애드립 음악을 아직도 못 잊는 분들이 적지 않다.

FM 음악의 음색은 뱅크 파일에 별도로 담겨 있었다. 수백 개의 악기 음색이 100~200KB대 크기에 담겨 있던 걸로 기억한다. 음악에서의 악기는 문자 문서에서 일종의 폰트와 같은 존재인 셈이다.
PC 통신의 음악 자료실에는 최신 유행가, 팝송, 게임 음악 따위의 ROL/IMS 파일들로 넘쳐났다. 누군가가 악보를 구해다가 노가다로 열심히 입력해서 만들었을 것이다. IMS 파일은 당시 PC 통신 프로그램의 최강자이던 <이야기>가 지원했으니 인지도 면에서 더 말이 필요없었다.

이에 덧붙여 ISS라고 해서 가사 파일이란 게 국내에서 제정되었는데, 곡이 진행되면서 글자색이 점진적으로 변하게 할 수 있었기 때문에 일종의 노래방 효과도 낼 수 있었다. 동영상으로 치면 자막 파일과 같은 존재이다.

※ 모듈 S3M, MOD

모듈 음악 파일은 기본적으로 음표 정보 기반 음악 파일 포맷이긴 한데, FM 방식과는 중요한 차이가 있다. 악기의 음색이 waveform 오디오 형태로 파일에 내장되어 있다는 것. 문서로 치면 폰트를 일일이 내장하고 있는 셈이다. 그래서 평균적인 파일 크기는 기본이 수백 KB는 먹고 들어가기 때문에 mid나 애드립 사운드보다는 큰 편이지만, 당시로서는 가격 대 성능비가 아주 우수하고 음질이 좋은 음악을 만들어낼 수 있었다.

다만 모듈 음악은 여전히 음악보다는 컴퓨터 지향적인 방식이고, 미디처럼 세계 균일 표준으로까지 승격되지는 못해서 오늘날은 WinAmp나 VLC 같은 일부 매니악한 프로그램이나 재생을 지원하는 마이너 포맷으로 명맥을 유지하게 됐다.

애드립 음악에 Visual Composer가 있다면, 모듈 음악 분야에는 Scream Tracker라는 금색 UI를 갖춘 유명한 소프트웨어가 본좌이다. 그리고 재생기로는 Inertia player이라고 전설적인 도스용 프로그램이 있었다. 개발자가 밝히기를 100% 어셈블리만 써서 작성했다고 하니 흠좀무.

※ 대세는 미디

그 반면 오늘날 대세는 역시 국제 표준인 미디이다. 본인은 윈도우를 쓰기 전에 도스 시절에는 애드립이나 모듈 음악만 접했지 미디 파일도, 재생기도 전혀 접하지 못했다. 하지만 미디라는 표준 자체는 굉장히 오래 전에 제정된 것이다.

심지어 1989-90년대를 풍미했던 페르시아의 왕자의 midisnd.dat 같은 파일을 들여다 봐도, 내부는 윈도우 미디어 플레이어로 재생 가능한 표준 미디 파일들의 모음이다! 그래서 인트로/엔딩 음악, 죽었을 때의 음악 따위를 쉽게 추출할 수 있다.

도스용 둠 1, 2의 배경 음악도 내부적으로는 미디 포맷이다. 사실, 그 전작인 울펜슈타인 3D도 데이터 파일을 들여다보지는 않았지만, 음악을 딱 들어 보면 미디인게 티가 난다.

미디에는 구체적인 음색에 대한 규정은 전혀 없기 때문에, 과거 애드립으로 허접하게 재생되던 음악도 미디인가 하면 오늘날 최첨단 노래방 기기에서 코러스까지 곁들여져 나오는 음악도 죄다 미디이다. 과거에는 미디 음악을 컴퓨터에서 제대로 들으려면 미디 카드가 필수였지만, 컴퓨터의 성능이 향상되면서 2000/ME부터는 윈도우 운영체제가 좀 그럴싸한 미디 신시사이저 소프트웨어를 내장하게 되었다.

하지만 요즘 게임들은 음악도 닥치고 wav나 mp3 통째로 내장이다. DirectMusic이 괜히 개발이 중단된 게 아니다. 현업 게임에서 쓰이질 않고 있는 컴포넌트이기 때문.

※ 애드립 음악 관련 추억: 옹 컴포저

1998년의 일이다. 옹 언욱 씨라고, 본인보다 나이는 한 학년 위이고 당시 고등학생이던 분이 <옹 컴포저(Ong Composer)>라는 프로그램을 개발했다. 쉽게 말해 애드립 음악 파일 편집기이다. 그런데 이분은 프로그래밍은 물론이고 음악, 그래픽까지 두루 본인과는 비교가 안 되는 진정한 엄친아였다. 그 열악한 16비트 볼랜드 C++로 슈퍼 VGA 그래픽(선 그리기, 점 찍기, 비트맵 -_-)과 사운드 제어 루틴을 어셈블리로 다 자체 제작하고 GUI 라이브러리에 심지어 스킨까지 혼자 다 만들었다... ㅎㄷㄷㄷㄷ;; 난 그런 쪽은 쥐뿔도 실력이 없으니 전적으로 공개 라이브러리에 의존했는데 말이다. ㅋㅋ

참고로, 컴퓨터 음악 프로그램은 Noteworthy Composer처럼 작정하고 위지윅에 최적화된 프로그램이 아닌 이상, 우리가 흔히 생각하는 것처럼 오선지에 콩나물을 그려 넣는 형태가 아니다. 스프레드시트에다가 가로줄 길이로 음표를 표현하는 아주 기계 친화적인 모습을 하고 있다. 아까 언급한 Visaul Composer나 Scream Tracker도 마찬가지. 이는 프로그래밍 언어 소스 코드에 우리가 종이에다 쓰는 수학식이 그대로(근호, 분수 등) 들어가는 게 아닌 것과 같은 이치이다.

그런데 본인도 응시했던 1998년 제 15회 정보 올림피아드 공모 부문에서 옹 컴포저는 입상을 못 했다. 이런 어마어마한 프로그램이 왜 입상을 못 했는지는 모르겠다. 그러나 이듬해, 16회 대회에서 이분은 옹 컴포저를 윈도우용으로 포팅한 옹 컴포저 2를 출품하여 금상을 받는다. 그 후의 이분 근황은 본인도 알지 못한다. 프로그래밍에다가 탁월한 예체능(그래픽/음악) 쪽 재능을 갖춘 전문가이다 보니, 게임 개발에 뜻이 있는 분이던 걸로 기억한다.

덧붙이자면 15회와 16회 대회 때는 고등부에 대상 수상작이 없었다. 그 후 17회에서 본인이 출품한 한글 입력기 1.0 버전이 대상을 차지했다.

※ 모듈 음악 관련 추억: BWSB 라이브러리

BWSB (Bells, Whistles, and Sound Boards)라고 어느 영국의 프로그래머가 개발한 프로그래밍 라이브러리가 있었는데, 이게 정말 물건이었다. 퀵베이직, 파워베이직, 볼랜드 C/C++, 볼랜드 파스칼 등에서 모듈 음악을 재생해 줬다. 셰어웨어이긴 하지만 공개용도 프로그램 종료 시에 copyright 메시지가 뜨는 것 말고는 별다른 제약이 없었다. 굉장히 잘 만들었고 문서화도 서양식 유머가 가미된 재미있는 문체로 되어 있었다. "이런 주의사항을 지키지 않으면 외계인이 쳐들어와 당신의 컴퓨터를 가져가 버릴 것이다" 식.

이 분야에서는 거의 독보적인 라이브러리가 아니었나 싶다. 하지만 왓콤이나 DJGPP 같은 32비트 컴파일러를 지원하지 못했던 게 아쉬운 점으로 남아 있다. 어셈블리 튜닝 코딩이 많다 보니, 소스의 이식성이 떨어져서 포팅이 어려웠던 듯하다.
하긴, DJGPP용으로는 알레그로라는 만능 게임 라이브러리가 있긴 했는데 이건 모듈 음악은 지원 안 하고 미디만 지원했다. 알레그로도 영국 사람이 만들었다.

Posted by 사무엘

2000년 7월 27일
반 년이 넘는 시간 동안 개발해 온 <날개셋> 한글 입력기 1.0 프로젝트를 완료하고 프로그램과 설명서를 교육청에 제출했다.

2000년 8월 30일
밤 11시 20분경, 기숙사 사감 선생님이 나를 불러 집에 전화가 왔다고 전해 주셨다. 그리고 무슨 대회 예선을 통과했다고 하는 일종의 힌트도 덧붙였다. 집에 전화해서 보니 아니나다를까 어머니께서 ICC(당시 정보 문화 센터.. KOI 주최 기관)에서 연락이 왔다고 전해 주셨다. 결과는 물론 합격이었다.
오! 이제까지 코딩한다고 겪은 고생과, 그 고통보다 더 컸던 기다림의 고통이 단번에 사라지는 순간이었다.

2000년 9월 1일, 7교시 수업을 듣고 바로 가방을 싼 뒤 담임 선생님을 만나고 나서 집으로 돌아갔다. 2차 심사 준비를 해야 하니까. 2년 전의 기적이 재현됐으니 난 뛸 듯이 기뻤다.

그리고 9월 2일, 오전 6시에 출발하는 서울 행 고속버스를 타고 나는 어머니와 함께 서울로 떠났다.
97, 98년때와는 달리 이번에는 2차 심사가 대학교가 아닌 ICC 본관에서 열렸다. 건물은 새로 지어져 있었고 무척 깔끔했다. 1년 반쯤 전에 여기 왔을 때와는 사뭇 다른 모습이었다.

넓은 홀에 도착했을 때는 아직 아침이었다. 몇몇 사람이 먼저 와서 기다리고 있었고, 나는 거기서 잠시 눈을 붙였다. 그러고 나서 나는 어머니와 점심을 먹었다. 오후 2시 20분이 되어서 나는 대기실로 들어가서 진행위원의 지시를 들었다. 특별히 하는 일 없이 몇 시간이 금방 흘러갔다.

나는 심사받는 15명 중 가장 먼저 심사받는 조에 걸렸다. 수험표를 받고 심사장으로 들어갔다. 카이스트, 고려대 교수를 비롯한 다섯 명의 교수들이 컴퓨터를 빙 둘러싼 가운데 설명을 해야 했기 때문에 약간 떨리긴 했지만, 난 준비한 슬라이드를 보여주면서 진지하게 프로그램 소개를 했다.

교수들이 주로 질문한 내용은 두벌식 자판에 대한 내 입력기의 호환성이었다. 나는 망설이지 않고 내 입력기의 장점을 강조하면서, 한글 기계화는 세벌식으로 가는 것이 타당하다고 말을 이었다.
곧이어 심사 위원들은 이 프로그램을 무슨 언어로 짰는지 묻고, 여기에 대한 지식을 언제부터 쌓아 왔는지 물었다. 난 물론 사실대로 대답했다.

이런 식으로 10분짜리 심사가 끝나고 나는 귀가하게 됐다. 그동안 조금도 떨지 않았고, 심사위원과 아주 평범하게, 부담없이 얘기를 나눴다. 시간이 내가 느낀 것보다 훨씬 빨리 갔음을 느낄 수 있었다.

2000년 9월 4일
아침 조회가 끝난 직후에 부랴부랴 ICC 홈페이지에 접속해 봤지만 별다른 소식은 없었다. 그런데 4층으로 올라가자 담임 선생님께서 내게 대상을 받았다고 전해 주셨다. 날 보더니 악수를 청하면서 “용묵아, 축하한다. 대상이더라.” 하고 말씀하셨다.
아니, 내가 컴퓨터실에 가 있던 사이에 선생님께서 먼저 교실에다 소식을 전하신 모양이었다. 급우들도 나를 보자 곧바로 축하 인사를 건네고, 이제 카이스트에 그냥 갈 수 있냐고 다그쳐 물었다.

-- 이 날은 네게 기념일이 될지니 네가 이 날을 평생 명절로 지키고 규례에 따라 그것을 영원토록 명절로 지킬지니라.
-- 보라, 김 용묵의 남은 행적 곧 그가 코딩을 하고 정올에서 입상한 과정은 그의 일기에 기록되어 있느니라.

당시 17회 대회 때 고등부에서는 총 92편의 작품이 출품되었다. 그 중 15편이 2차 심사 대상자가 되었다.
참고로, 대회 결과가 발표된 지 얼마 안 되어 ICC 홈페이지엔 이런 글도 올라와 있었다.

본인은 심사 받으면서 저런 일을 전혀 겪지 않았으며(2~3명 중의 하나였군), 아주 무난하고 자연스럽게 내 프로그램 소개를 하고 질문에 답변도 하고 왔다. 또한 조원들 중에 가장 먼저 심사를 받았기 때문에 다른 사람들의 심사 장면은 보지도 못했다. 가히 best 케이스...;;
솔직히 말해서 내 프로그램은 대리 개발을 할래야 할 수가 없는 아이템이었으니 말이다.

대회 결과가 나오긴 했는데.. 문제가 있었다.
카이스트는 다른 대학보다 전형을 굉장히 일찍 하기 때문에, 본인은 이 대회의 결과를 아직 모르는 상태에서 원서를 '일반 지원자'로 제출해 버린 상태였다.

그런데.. 카이스트는 추후에 발표된 이 대회 결과를 받아들였고, '일반 지원자'이던 본인의 등급을 '지정 대회 우수 입상자'로 업그레이드해 줬다. (지금은 그런 대인배스러운 제도는 이미 옛날에 없어졌음. ㄲㄲ)
나중에 카이스트에서 본인의 고등학교로 1차 서류 전형 합격자 명단을 팩스로 보내 줬는데, 그때 본인의 이름은 인쇄체가 아니라 맨 끝에 손글씨로 적혀 있었다는 전설이 전해진다.

그리고 그 <날개셋> 한글 입력기 1.0은 2, 3, 4를 거쳐서 10년이 지난 지금은.. 5.65까지 버전이 올라갔다. 5.65 버전이 일종의 개발 10주년 기념작이다. 소스 코드 줄 수는 10년 전에 비해서 5배가 넘게 불어났고, 기술 수준은 당연히 그때와는 비교가 되지 않는다.

학부 시절엔 이 프로그램 개발과 관련된 연구만으로 5학점을 먹었다. 3학점짜리 학부 졸업 논문과 1학점짜리 개별 연구 두 건(TSF 모듈 개발, 그리고 3.0 아키텍처 연구). 이제 대학원에 가서도 써먹을 예정이다. 왜냐 하면 학부 졸업 후에도 또 논문 쓸 만치 연구 실적은 추가로 쌓였기 때문이다. 그리고 사실은 <날개셋> 말고도 전산 기술을 접목시킨 다른 한글 관련 연구 주제도 생각하고 있는 게 있다.

프로그램 개발하면서 나름대로 아래와 같은 손발리 오그라들 것 같은 말도 들었다. 앞으로도 <날개셋> 한글 입력기의 무궁한 발전을 위하여, 버전 6.0을 향하여 "cheers!"를 외쳐 본다.

Posted by 사무엘

구미와 더불어 본인에게 21세기 이전에 기차 타고 방문한 추억이 있는 곳은 바로 수원이다. 고등학교 시절, 인텔 ISEF 참가 준비와 교육 때문에 한동안(1999년 3월~4월).. 무려 주말마다 성균관 대학교 수원 캠퍼스를 찾은 적이 있기 때문이다. 이 거사를 치르느라 그 옛날에 휴대전화까지 잠깐 구경하기도 했다.

그러고 보니 구미와 삼성 하니까 둘 다 경부선 철도가 지나고 삼성과 밀접한 관계가 있는 산업 도시라는 공통점이 있네? 뭐 그건 그냥 우연의 일치인 것 같고.

저것도 지금 생각하면 그야말로 상상도 할 수 없는 엄청나고 값진 경험인데, 내가 그때는 지리와 교통 쪽 감각이 백지나 다름없는 상태여서 당시에 대한 기록과 기억이 전혀에 가깝게 없다. ㅠ.ㅠ 새마을호나 무궁화호 같은 관념도 없어서 어떤 열차는 좀 으리으리하고 고급스러운데, 어떤 열차는 좌석도 작고 입석 승객까지 있어서 혼잡하다는 식의 인식만 있었다.
희미한 기억을 더듬어 보면, 집에 돌아갈 때 기차를 잘못 타서 삽질한 적도 있었다.

수원 역에서 성균관대 역까지는 전철로 금방이다. 출구로 나가면 곧바로 야구 연습장이 보였고, 언덕을 내려서 조금 걸어가면 성균관 대학교 이공계 대학 캠퍼스가 나왔다. 당시 지도 교수는 워낙 유명한 분이니 실명을 거론하겠다. 황 대준 교수님의 멀티미디어 연구실에 있었다. 그러면서 거기 랩에 있던 대학원생 형들과도 부대꼈고, 아마 이분들이 지내는 기숙사 내지 대학원생 아파트 구경도 했던 것 같다. 난 그로부터 10년도 더 지나서 이제야 대학원으로 고고씽이구나. ㅠ.ㅠ

그때가 본인 역시 이제 막 도스+C에서 벗어나 윈도우 API+MFC를 같이 공부하던 시절이었기 때문에, 이때의 대회 준비 경험은 본인의 실력 향상에도 큰 도움이 됐다. 단편적인 프로그래밍 지식뿐만이 아니라 영어 프레젠테이션, 대인 관계, 대학과 대학원의 분위기 같은 것들도.
내가 조금만 더 세상 보는 식견이 넓었으면 그때 마주쳤던 분들에게 훨씬 더 예쁘게-_- 보이고, 그분들에게서 더 많은 걸 배워 올 수도 있었을 텐데 그러지 못한 것은 늘 아쉬움으로 남는다.

대학 시절 한때는, 밤에 자다가 <날개셋> 한글 입력기로 ISEF에 다시 나가는 괴상한 꿈을 꾸기도 했다. 그건 아주 한국적인 소재인 데다, 고3 때 입상한 작품이기 때문에 그런 일은 현실에서는 절대 불가능한 일이다. 사실, 본인이 ISEF 첫 출전 티켓을 딴 것도, 전적으로 당시 본인보다 더 뛰어난 작품을 만든 학생은 이듬해에 대학에 가 버렸기 때문이었다.

그 당시는 아직 인지도가 부족한 관계로 ISEF 참가 경험은 IOI(국제 정보 올림피아드) 참가와는 달리 입시에서 뭔가 가산점으로 인정이 안 되었다. 그런데 그게 본인에게는 역설적으로 기회로 작용했다. ISEF에 갔다 온 후에도 아예 고3 때 과거 ISEF 작품과는 관계가 없는 작품을 하나 또 만들어서 그건 아예 대상을 받아 버렸기 때문이다. 정올 역사상 전무후무한 기록이 아닐지? (경시부였다면 불가능한 일. IOI 참가자는 이제 상급 학교에 진학하기 전까지 KOI에 또 응시할 수 없다.)

첫 참가자인 본인 이후로 ISEF 참가자 교육은 카이스트에서 이뤄지고 있는 걸로 본인은 알고 있다. 그리고 혼자만 가는 게 아니라 최하 두 팀이 가는데, 동 대회에 출전하는 ISEF 참가자들끼리는 서로 그렇게 자주 교류한다거나 친한 사이가 되지는 않는다고 들었다. (후배에게서 들은 증언) 차라리 서로 다른 기수의 대회에 참가한 선후배끼리가 친해진다나?

정보 올림피아드와 관련하여 본인이 방문한 적이 있는 대학으로는 성균관대 말고도 KOI 경시부가 당시 치러졌던 서울대, 그리고 공모부 2차 심사가 열렸던 중앙대(1997)와 숭실대(1998)가 있다. 경시부의 경우, 지방에서 온 애들은 대회 전날의 예비 소집에 참석한 후 무려 학교 근처의 여관에서 자기도 했는데...;;;

지금은 그런 행사들이 대학에서 개최되지 않고 백범 기념관이라든가 정보화 진흥원 본관에서 개최되는 걸로 안다. 기관 이름도 처음엔 정보 문화 센터(ICC)이다가 정보 문화 진흥원(KADO)을 거쳐 지금은 정보화 진흥원(NIA)으로 참 자주 바뀌었다.
옛날에는 역대 수상자를 조회하면서 공모부의 경우 작품명까지 볼 수 있었는데 그건 사생활 보호(?) 차원에서 삭제한 모양이다.

어쨌든 결론은!
본인의 인생에서 정올과 관련된 옛 추억에도 철도가 조금이나마 끼여 있다. 그걸 이제 와서 추적하려고 하니까 쉽지 않다.

Posted by 사무엘

벌써 10년 전의 일이군요. ㅎㄷㄷㄷ
완전 책을 만들어서 출품했었습니다. 아래아한글 97 이용.

Posted by 사무엘

2000년, 제 17회 한국 정보 올림피아드 공모 부문 대상

그리고 이건 ISEF 참가자용 명찰..

Posted by 사무엘