퇴근길에 문득 든 아주 기초 수학 생각이다.
아래 그림은 포물선 2개 x^2+2*x (x=-2..0), -x^2+2*x (x=0..2)와, sin(x*PI/2) (x=-2..2)를 한데 포개 놓은 것이다.
원래 sin, cos 부류의 삼각함수는 주기가 2*PI인데, 이를 4로 좁혀 놓았다.
이렇게 보니까 포물선도 싸인파 곡선과 형태가 생각보다 꽤 비슷해질 수 있다는 걸 느꼈다.
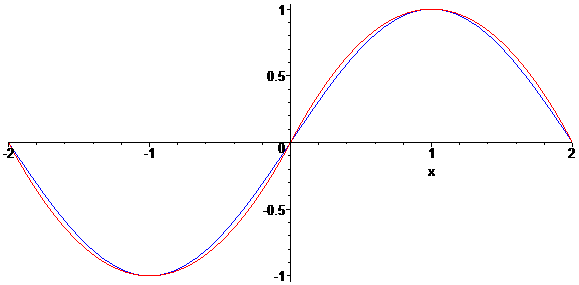
0부터 2까지 구간의 넓이를 정적분으로 구해 보면 이차함수인 포물선의 면적은 4/3인 반면, 진짜 싸인파의 면적은 4/PI이다. 즉, 포물선에 속하는 면적이 약간 더 크다.
그러나 이 두 곡선은 비슷하게 생겨도 그 본질은 굉장히 다르다. 미분을 해 보면 안다. 이들의 도함수를 그래프로 그리면 다음과 같다.
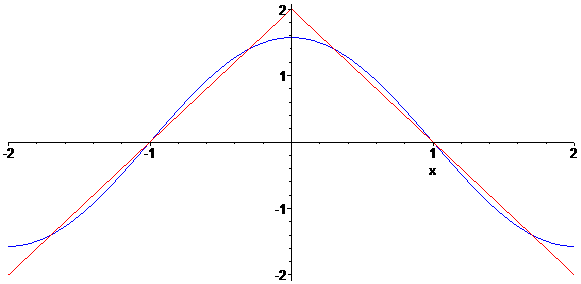
싸인파는 도함수도 기준 위치와 진폭만 다를 뿐, 여전히 전구간이 미분 가능한 매끄러운 싸인파이다.
그러나 두 포물선을 인위적으로 연결한 함수는 도함수가 직선으로 바뀌었고, x=0 지점은 연속이긴 하지만 기울기의 좌극한과 우극한의 값이 서로 달라서 미분이 불가능한 점이 되었다. 마치 절대값이 들어있는 일차함수처럼 된 셈이다.
이걸 또 미분하면 어떻게 될까?
싸인파는 역시 또 싸인파이지만 저 직선은 아예 양수 아니면 음수의 상수함수로 바뀌고, x=0 지점은 이제 연속이지도 않게 된다. 마치 인간이 만든 아무리 매끄럽고 뾰족한 바늘도 확대하고 또 확대해서 보면 울퉁불퉁한 표면이 드러나듯이 말이다.
우리가 자연에서 흔히 볼 수 있는 물체의 운동 양상은 관성에 의한 등속 직선, 아니면 힘을 한 쪽으로 균일하게 받는 포물선 형태가 있다. 하지만 출렁이는 물결이나 음파 같은 진동은 삼각함수에 속하는 싸인파가 자연스러운 움직임이다. 오히려, 포물선 두 개를 갖다붙인 것에 불과해서 미분하면 딱딱한 절대값 직선으로 바뀌어 버리는 곡선이야말로 인위적이고 부자연스러운 형태인 것이다.
왜 싸인파가 자연스러운 움직임일까?
삼각함수는 무한소나 무한대로 발산하지 않고 주기를 갖고 -1에서 1 사이를 한없이 진동만 한다.
그러면서도 전구간이 단절 없이 연속이고 미분 가능하다. 미분을 해도 심지어 도함수조차 형태를 바꾸면서 주기적으로 자기 자신으로 돌아오기를 반복하기 때문이다.
내가 수학적인 통찰력이 부족해서 그 원리를 다 '이해'와 '실감'은 못 하겠지만, 적어도 이런 함수는 돼야 정말 매끄러움의 본질을 수학적으로 표현한 게 아닌가 하는 막연한 추측까지는 한다.
해석학적으로 볼 때 x^n의 x에 관한 미분은 n*x^(n-1)로 떨어진다. 지수함수 exp는 알다시피 (1/ n!)*x^n의 무한합으로 정의되어, x에 대해 미분하더라도 예전항이 바로 다음항의 미분 결과와 같은 꼴이 되는 형태이다.
그런데, 삼각함수인 sin과 cos는 exp를 홀수승 항과 짝수승 항으로 분할함과 동시에 각 항의 부호를 또 +, -로 교대로 오고 가게 바꾼 형태이다. 그래서 함수가 무한대나 무한소로 발산하지 않고 진동하게 된다. 신기하기 그지없다.
미적분학을 공부하면 삼각함수와 더불어 쌍곡선함수라는 물건도 배우게 된다.
얘는 sin과 cos에다가 h를 붙여서 sinh, cosh처럼 쓰는데, 지수함수를 이루는 무한급수에서 각각 홀수승항과 짝수승항만 쪼개서 취한 함수이다. 삼각함수와의 차이는 부호 스위칭이 없다는 점이 전부다.
그래서 쌍곡선함수는 비록 그래프의 모양은 삼각함수와 완전히 다르지만 삼각함수와 굉장히 비슷한 특성을 갖게 된다. sinh와 cosh는 미분하면 부호 스위칭이 없이 서로 상대편으로만 탈바꿈하며, 삼각함수의 덧셈정리와 비슷한 특성도 가진다. 삼각함수가 cos(x)^2 + sin(x)^2 = 1이듯이 cosh(x)^2 - sinh(x)^2 = 1이다. 전자가 원스럽다면 후자는 정말 쌍곡선스러운 형태이지 않은가?
쌍곡선함수는 사실상 수학 해석학적인 의미 때문에나 배우지, 삼각함수에 비해 실생활에서 유용한 구석은 별로 없는 것 같다. 그러나 얘도 자연에서 의외로 중요한 곳에서 자주 볼 수 있다. cosh가 바로 현수선의 방정식을 나타내는 함수이기 때문이다.
현수선이란 밀도가 균일한 줄이 자기 길이보다 짧은 간격으로 양 끝이 어떤 중력장 안에 매달렸을 때, 자신의 무게로 인해 중력의 방향(아래)으로 축 늘어짐으로써 형성되는 선을 말한다.
이것도 포물선과 비슷해 보여서 혼동되기 쉽지만, 포물선하고는 수학적인 성질이 완전히 다르다. 현수선은 증가의 폭이 이차함수가 아니라 지수함수와 같은 스케일이다.
알고 보면 아치도 포물선이 아니라 현수선을 뒤집은 모양이다. 현수선 모양으로 구조물을 건설하는 게 모양이 역학적으로 가장 안정적으로 형성된다고 한다.
왜 현수선이 cosh 함수의 형태로 형성되는지 수학적으로 증명하려면 물리학, 미적분학 등 여러 방면의 이론이 동원돼야 하지 않을까 싶다.
어찌 보면 당연한 말이지만, 현수선은 일부만 잘라 내도 그 모양이 그대로 유지된다. 다시 말해 U자 모양으로 된 현수선의 양 끝의 일부를 잘라내서 u부분만 잡고 있더라도 기존 부위가 받는 힘은 변함없으며, 그 구간의 선 모양이 바뀌지 않는다는 뜻이다.
삼각함수와 쌍곡선함수가 각자 자기 분야에서 포물선과는 다른 매끄러움, 출렁거림 등을 표현하고 있다는 게 경이롭다.
자연 현상으로부터 얻은 물리량이라는 게 태생적으로 연속적인 데이터의 형태이다 보니, 물리학의 발전을 위해서는 수학, 특히 미적분학의 발전이 반드시 선행되어야 했다는 게 느껴진다.
Posted by 사무엘


