김 용묵의 절대공간 - 블로그

'초등함수'에 속하는 '초월함수'들 중에 지수함수인 e^x는 미분을 하던 적분을 하던.. 도함수나 부정적분이 전부 자기 자신과 동일한 굉장히 특이한 기본 함수이다.
지수는 저렇고, 삼각함수/쌍곡선함수는 그냥 답정너 정의에 가깝게 미분-적분 순환고리를 그냥 외운다.
그럼 e^x의 역함수인 ln x는 부정적분이 과연 어찌 될까?

ln x는 도함수가 1/x라는 간단한 형태로 정의되는 덕분에, '부분적분'으로 부정적분을 구하는 아주 교과서적인 예로 다뤄진다.
부분적분은 곱의 미분법으로부터 유도되어 두 함수 F, G의 곱에 대해

F(x)G(x) = ∫ F'(x)G(x) dx + ∫ F(x)G'(x) dx

가 된다는 원리이다. 보통은 저것보다는 순서를 바꿔서

∫ F'(x)G(x) dx = F(x)G(x) - ∫ F(x)G'(x) dx

요런 형태로 더 소개되는 편이다.
ln x의 경우, 위의 부분적분에서 F는 그냥 x로, G는 ln x를 집어넣으면 바로 풀린다. 그러면 F'(x)는 1이라는 상수가 되고 G'(x)는 1/x가 되므로

∫ ln x dx = x*ln x - ∫ x/x dx = x*ln x - x = x(ln x - 1)

이렇게 답이 구해진다. x*(ln x)' 가 x/x로 바뀌어서 1로 상쇄되는 것이 백미이다.;;

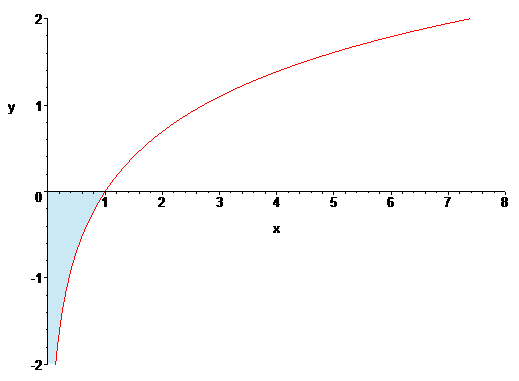
그럼 ln x의 0..1 정적분의 값은 얼마일까? 다시 말해 위의 그래프에서 선이 y축의 0 아래로 뚝 떨어지는 구간의 면적은 얼마일까?
저 역도함수에다가 0과 1을 대입해서 차를 구하면 -1임을 알 수 있다. 그러나 더 직관적으로 아는 방법도 있다.
저 구간은 ln x의 역함수인 exp(x)에서 x의 음수 구간 면적과 동일하기 때문이다.

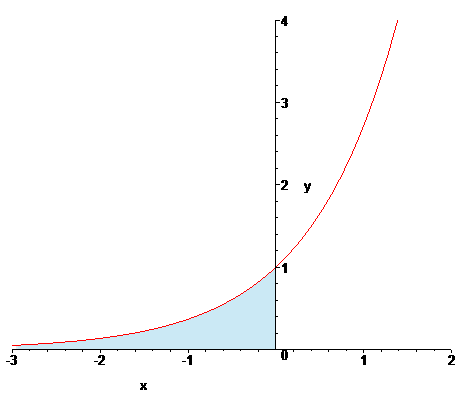
그러니 exp(x)를 0부터 -∞까지 적분해 봐도 동일한 값을 더 쉽게 구할 수 있다. exp는 그냥 자기 함수에다 값을 대입하는 것만으로 적분값을 구할 수 있으니 말이다.

그리고 더 흥미로운 사실이 있다.
ln x의 부정적분인 x(ln x - 1)의 의미는 바로..
저 X축의 x, 그리고 Y축의 ln x라는 직사각형에서.. 맞은편의 역함수 exp(ln x) 구간의 면적을 뺀 나머지 면적이라는 것이다. -x의 의미는 바로 -exp(ln x)라는 것..!!

부분적분에서 곱을 구성하는 두 함수 중의 하나가 그냥 x 자체인 덕분에, 기하학적으로 이런 의미까지 지니게 된 셈이다.
앞서 부분적분 식에서는 x가 x*(1/x)를 적분해서 얻어졌었는데.. 여기서는 exp와 ln이 상쇄되어 얻어졌다는 게 흥미롭다.

이런 부분적분은 삼각함수 등 다른 초월함수들의 '역함수'의 부정적분을 구할 때도 요긴하게 쓰인다.
부분적분의 특성상 원함수의 도함수도 알아야 하는데, 그건 역함수의 미분법을 동원해서 구하면 된다.

다음으로, ln x를 넘어서 (ln x)^2의 정적분을 구하려면?
부분적분 패턴에서 F'(x)와 G(x)를 모두 ln x로 잡으면 된다. 그러면 F(x)는 x*(ln x -1)에 대응하고, 최종적으로는 아래와 같은 복잡한 식이 도출된다.

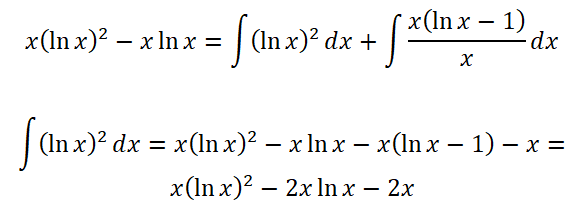
이를 일반화해서 (ln x)^n의 부정적분은

x*(ln x)^n - a*x*(ln x)^(n-1) + b*x*(ln x)^(n-2) ... +- z*x*(ln x) +- z*x + C (적분상수)

이런 꼴이 된다. 모든 항에 x는 기본으로 붙어 있고 그 다음에 (ln x)의 n승에 대한 항이 형성되어 항의 수는 총 n+1개..
부호는 -와 +가 번갈아가며 바뀐다.
맨 앞의 제일 고차항인 (ln x)^n의 계수는 언제나 1이지만, 그 다음 항인 a...z로 갈수록 n과 n-1, n-2... 가 차례로 곱해져서 n=2일 때는 2 2.. n=3일 때는 3 6 6, n=4일 때는 4 12 24 24... 이렇게 계수가 정해진다.

그러므로 0에서 1까지의 정적분 값은 n의 홀짝 여부에 따라 부호가 교대로 바뀌는(홀-음수, 짝-양수) n!이 된다.
원함수에다가 미리 -를 씌운 (-ln x)^n라고 해 주면 0..1 정적분은 간단하게 n!로 떨어진다. n이 홀수승일 때는 (ln x)^3의 값이 음수이던 것이 - 부호를 만나서 양수로 바뀌고, 짝수승일 때는 거듭제곱이 음수를 양수로 바꾸기 때문에 팩토리얼이 언제나 양수로 나오는 것이 보장된다.

로그의 거듭제곱의 적분이 팩토리얼과 관련이 있다니.. 신기한 노릇이다. 이 덕분에 지수뿐만 아니라 팩토리얼조차도 정의역이 단순히 자연수에 국한되지 않고, 지수함수와 적분와 동급인 실수 영역에 연속적인 형태로 정의될 수 있게 됐다.

(-ln x)^n의 0..1 정적분은 치환적분 기법을 동원해서 다음과 같은 형태로 바꿀 수 있다.

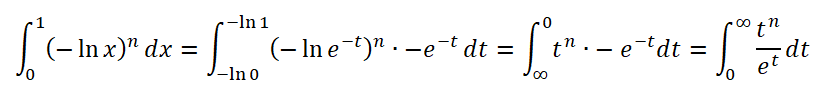
뭐.. 로그를 쓰면 구간이 0~1인데, 지수를 쓰면 구간이 0~무한대로 바뀐다는 차이가 있다. ㄲㄲㄲ
요 함수가 일명 '감마'(Γ) 함수라고 불린다. 단, 감마 함수는 모종의 이유로 인해 팩토리얼과 완전히 같지는 않아서 Γ(n+1)의 값이 n!에 대응한다.

x^x은 0일 때와 1일 때의 함수값이 동일하고, 그 사이엔 함수값이 살짝 작아졌다가 1 이후부터 폭발적으로 커진다.
감마 함수도 양의 실수 구간에서는 이와 비슷한 성질이 있어서 1과 2일 때의 함수값이 동일하다. 그 사이에는 함수값이 약간 작아졌다가 2 이후부터 폭발적으로 커진다.

단, x^x는 미분을 통해 그 최소값을 해석적으로 정확히 구할 수 있는 반면, 감마 함수는 대략 x≒1.46163에서의 최소값 0.88560...을 수치해석으로 구할 뿐이다. 이 수의 정확한 특성은 알려져 있지 않은 것 같다.
그런데.. 감마 함수는 소수점이 .5 인 수.. 다시 말해 자연수에다가 1/2이 첨가된 수에 대해서는 π(원주율)의 제곱근의 배수인 그 무언가를 되돌린다. 이런 것도 여느 지수함수나 그쪽 바리에이션에서는 발견할 수 없는 면모이다.

특히 Γ(1/2)의 값은 딱 정확하게 sqrt(pi)인데, 이것은 정규분포 함수의 원형인 e^(-x^2)의 전구간 적분 면적과 동일한 값이다.
1/2일 때 감마 함수 적분식은 적분변수 x를 sqrt(t)로 치환하면 딱 정확하게 e^(-x^2)의 전구간 적분과 동일한 식이 나오기 때문이다. ㅎㄷㄷㄷ..

물론 e^(-x^2)은 부정적분이 초등함수의 형태로 표현되지 않는 괴상한 물건이며, 가우스 적분이라는 완전히 새로운 방법론을 동원해야 전체 면적만을 구할 수 있다. 이 과정이 뱅그르르 회전과 관계가 있기 때문에 갑자기 원주율이 튀어나오는 것이다. 하지만 이건 이 글의 범위를 한참 넘어서기 때문에 더 자세한 얘기를 생략하겠다.

다시 본론으로 돌아오면.. 로그의 n승을 정적분 했더니 n팩토리얼이 튀어나왔다. 반대로 팩토리얼 값에 로그를 씌운 것도 로그와 관련이 있다. log N!은 수가 증가하는 정도가 N log N과 얼추 비슷하다.
왜 그런가 하면 N!은 1*2*3...*N이니 log N!은 log 1+log 2+log 3+ ...log N과 같기 때문이다. 그리고 이건 log N에 대한 적분에다 근사시킬 수 있으며, 그 부정적분에는 N log N이 포함되어 있다.

컴퓨터 알고리즘 중에서 정렬이라는 건 n개의 원소들을 나열하는 순열 최대 n!개의 가짓수 중에서 오름차순/내림차순 순서를 만족하는 것을 찾아내는 과정이다. 그런데 비교 연산을 한 번 할 때마다 그 가짓수를 이분 검색 하듯이 최대 절반으로 줄일 수 있다.

그러니 가짓수도 팩토리얼로 폭발적이고, 매 단계마다 가짓수를 줄이는 규모도 지수로 폭발적인데.. 결국 비교 연산을 수행하는 정렬 알고리즘의 이론적인 시간 복잡도는 팩토리얼의 로그급인 n log n으로 귀착되는 것이다.

팩토리얼 내지 팩토리얼의 로그를 근사하는 공식을 더 엄밀하게 파고들면 n log n에다가 다른 자잘한 항들도 여럿 붙는다. 이런 건 감마 함수를 변형해서 만들어지는데, '스털링의 근사 공식'이라고 한다.
애초에 x^n * e^(-x)도 e^(n ln x - x)로 바뀌니, n log n이라는 결론이 달라지지는 않는다.

이상이다. 로그에 이렇게 심오한 의미가 많이 담겨 있는 줄 몰랐다.;; 얘기가 꼬리에 꼬리를 물고 이어지는데, 로그의 밑 얘기만 하고 글을 맺도록 하겠다.

이공계에서 쓰이는 로그의 밑은 사실상 딱 세 종류.. 2, e, 아니면 10이라고 보면 되겠다.
2는 컴퓨터과학 전산학에서 특별히 아주 좋아하는 숫자이고, e는 지금까지 봐 왔듯이 천상 수학 미적분 해석학 전용이다. 10은 10진법과 관계가 있다 보니 데시벨이나 pH (산/염기 지수) 같은 로그 기반의 현실 과학 단위에서 쓰인다. 단, 복소해석학으로 가서 로그를 복소수 범위로 확장하면.. 0과 1만 빼고 -1이나 i조차 로그의 밑이 될 수 있으니 참 ㅎㄷㄷ하다.

현실에서 엄청 큰 측정값을 표기할 일이 있으면, 어지간해서는 메가· 기가· 테라· 페타 같은 접두사를 동원해서 자릿수를 줄이는 걸로 퉁칠 것이다. 아예 로그를 동원해서 자릿수를 후려친다는 건 정말 그 분야에서 얻을 수 있는 측정값의 스케일이 0의 개수 자릿수 차원에서 극단적으로 널뛰기 한다는 걸 뜻한다.

원래는 log 다음에 아래첨자로 밑을 일일이 써 주는 게 정석이다. 그러나 쓰이는 밑이 분야별로 저렇게 뻔히 답정너이니.. 그런 번거로운 표기는 잘 쓰이지 않는다. 밑이 e인 로그는 자연로그라고 해서 그냥 ln이라고 쓰는 정도?
밑을 생략한 log 표기는 밑이 무엇이건 중요하지 않고, 수가 증가하는 게 log 스케일이라는 것만이 중요할 때 쓰인다. 앞서 언급했던 시간 복잡도 표기처럼 말이다.

Posted by 사무엘

퇴근길에 문득 든 아주 기초 수학 생각이다.
아래 그림은 포물선 2개 x^2+2*x (x=-2..0), -x^2+2*x (x=0..2)와, sin(x*PI/2) (x=-2..2)를 한데 포개 놓은 것이다.
원래 sin, cos 부류의 삼각함수는 주기가 2*PI인데, 이를 4로 좁혀 놓았다.
이렇게 보니까 포물선도 싸인파 곡선과 형태가 생각보다 꽤 비슷해질 수 있다는 걸 느꼈다.

0부터 2까지 구간의 넓이를 정적분으로 구해 보면 이차함수인 포물선의 면적은 4/3인 반면, 진짜 싸인파의 면적은 4/PI이다. 즉, 포물선에 속하는 면적이 약간 더 크다.

그러나 이 두 곡선은 비슷하게 생겨도 그 본질은 굉장히 다르다. 미분을 해 보면 안다. 이들의 도함수를 그래프로 그리면 다음과 같다.

싸인파는 도함수도 기준 위치와 진폭만 다를 뿐, 여전히 전구간이 미분 가능한 매끄러운 싸인파이다.
그러나 두 포물선을 인위적으로 연결한 함수는 도함수가 직선으로 바뀌었고, x=0 지점은 연속이긴 하지만 기울기의 좌극한과 우극한의 값이 서로 달라서 미분이 불가능한 점이 되었다. 마치 절대값이 들어있는 일차함수처럼 된 셈이다.

이걸 또 미분하면 어떻게 될까?
싸인파는 역시 또 싸인파이지만 저 직선은 아예 양수 아니면 음수의 상수함수로 바뀌고, x=0 지점은 이제 연속이지도 않게 된다. 마치 인간이 만든 아무리 매끄럽고 뾰족한 바늘도 확대하고 또 확대해서 보면 울퉁불퉁한 표면이 드러나듯이 말이다.

우리가 자연에서 흔히 볼 수 있는 물체의 운동 양상은 관성에 의한 등속 직선, 아니면 힘을 한 쪽으로 균일하게 받는 포물선 형태가 있다. 하지만 출렁이는 물결이나 음파 같은 진동은 삼각함수에 속하는 싸인파가 자연스러운 움직임이다. 오히려, 포물선 두 개를 갖다붙인 것에 불과해서 미분하면 딱딱한 절대값 직선으로 바뀌어 버리는 곡선이야말로 인위적이고 부자연스러운 형태인 것이다.

왜 싸인파가 자연스러운 움직임일까?
삼각함수는 무한소나 무한대로 발산하지 않고 주기를 갖고 -1에서 1 사이를 한없이 진동만 한다.
그러면서도 전구간이 단절 없이 연속이고 미분 가능하다. 미분을 해도 심지어 도함수조차 형태를 바꾸면서 주기적으로 자기 자신으로 돌아오기를 반복하기 때문이다.
내가 수학적인 통찰력이 부족해서 그 원리를 다 '이해'와 '실감'은 못 하겠지만, 적어도 이런 함수는 돼야 정말 매끄러움의 본질을 수학적으로 표현한 게 아닌가 하는 막연한 추측까지는 한다.

해석학적으로 볼 때 x^n의 x에 관한 미분은 n*x^(n-1)로 떨어진다. 지수함수 exp는 알다시피 (1/ n!)*x^n의 무한합으로 정의되어, x에 대해 미분하더라도 예전항이 바로 다음항의 미분 결과와 같은 꼴이 되는 형태이다.

그런데, 삼각함수인 sin과 cos는 exp를 홀수승 항과 짝수승 항으로 분할함과 동시에 각 항의 부호를 또 +, -로 교대로 오고 가게 바꾼 형태이다. 그래서 함수가 무한대나 무한소로 발산하지 않고 진동하게 된다. 신기하기 그지없다.

미적분학을 공부하면 삼각함수와 더불어 쌍곡선함수라는 물건도 배우게 된다.
얘는 sin과 cos에다가 h를 붙여서 sinh, cosh처럼 쓰는데, 지수함수를 이루는 무한급수에서 각각 홀수승항과 짝수승항만 쪼개서 취한 함수이다. 삼각함수와의 차이는 부호 스위칭이 없다는 점이 전부다.

그래서 쌍곡선함수는 비록 그래프의 모양은 삼각함수와 완전히 다르지만 삼각함수와 굉장히 비슷한 특성을 갖게 된다. sinh와 cosh는 미분하면 부호 스위칭이 없이 서로 상대편으로만 탈바꿈하며, 삼각함수의 덧셈정리와 비슷한 특성도 가진다. 삼각함수가 cos(x)^2 + sin(x)^2 = 1이듯이 cosh(x)^2 - sinh(x)^2 = 1이다. 전자가 원스럽다면 후자는 정말 쌍곡선스러운 형태이지 않은가?

쌍곡선함수는 사실상 수학 해석학적인 의미 때문에나 배우지, 삼각함수에 비해 실생활에서 유용한 구석은 별로 없는 것 같다. 그러나 얘도 자연에서 의외로 중요한 곳에서 자주 볼 수 있다. cosh가 바로 현수선의 방정식을 나타내는 함수이기 때문이다.

현수선이란 밀도가 균일한 줄이 자기 길이보다 짧은 간격으로 양 끝이 어떤 중력장 안에 매달렸을 때, 자신의 무게로 인해 중력의 방향(아래)으로 축 늘어짐으로써 형성되는 선을 말한다.
이것도 포물선과 비슷해 보여서 혼동되기 쉽지만, 포물선하고는 수학적인 성질이 완전히 다르다. 현수선은 증가의 폭이 이차함수가 아니라 지수함수와 같은 스케일이다.

알고 보면 아치도 포물선이 아니라 현수선을 뒤집은 모양이다. 현수선 모양으로 구조물을 건설하는 게 모양이 역학적으로 가장 안정적으로 형성된다고 한다.
왜 현수선이 cosh 함수의 형태로 형성되는지 수학적으로 증명하려면 물리학, 미적분학 등 여러 방면의 이론이 동원돼야 하지 않을까 싶다.

어찌 보면 당연한 말이지만, 현수선은 일부만 잘라 내도 그 모양이 그대로 유지된다. 다시 말해 U자 모양으로 된 현수선의 양 끝의 일부를 잘라내서 u부분만 잡고 있더라도 기존 부위가 받는 힘은 변함없으며, 그 구간의 선 모양이 바뀌지 않는다는 뜻이다.

삼각함수와 쌍곡선함수가 각자 자기 분야에서 포물선과는 다른 매끄러움, 출렁거림 등을 표현하고 있다는 게 경이롭다.
자연 현상으로부터 얻은 물리량이라는 게 태생적으로 연속적인 데이터의 형태이다 보니, 물리학의 발전을 위해서는 수학, 특히 미적분학의 발전이 반드시 선행되어야 했다는 게 느껴진다.

Posted by 사무엘