이전 글들에서는 현수선 얘기를 하면서 한창 쌍곡선함수 얘기를 늘어놨는데, 이 글에서는 분위기를 바꿔 정통(?) 삼각함수 얘기를 좀 하겠다.
수학에서 다루는 많고 많은 곡선 중에는 “원을 직선 위에서 굴릴 때 그 원에 놓인 정점이 그리는 궤적”이란 게 있다. 이걸 ‘사이클로이드’라고 한다.
반지름 r인 원이 (0, r) 위치에 놓여 있다. 그리고 궤적을 추적하고자 하는 점은 처음에 바닥의 원점 (0, 0)에 있다고 치자.
수학 좌표계는 x의 양의 방향이 오른쪽이고 y의 양의 방향은 위쪽이다. 이 상태로 원이 x의 양의 방향으로 굴러가려면 시계 방향으로 굴러가야 하며, 각도는 처음에 270도에서 시작했다가 줄어들어야 한다. 각도가 늘어나는 방향은 반시계 방향이기 때문이다.

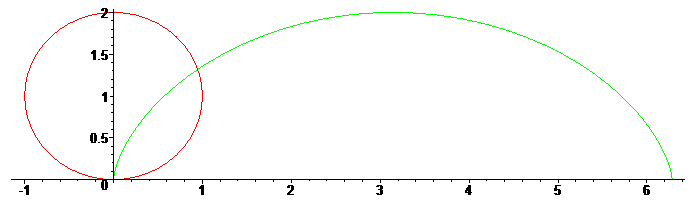
즉, (cos(3π/2 - θ), sin(3π/2 - θ)+1) 정도 될 텐데..
cos(3π/2 - θ)는 sin(-θ) → -sin(θ)로 간소화시킬 수 있다.
sin(3π/2 - θ)도 -cos(θ)로 간소화시킬 수 있다.
이건 원이 제자리에서만 빙글빙글 도는 상황이다.
실제로 굴러간다는 조건을 추가하면 원은 아주 단순하게 x축의 양의 방향으로 r*θ만치만 이동하게 된다. 원의 전체 둘레는 2πr이고 θ는 각도 겸 원호의 둘레와 정확하게 대응하기 때문이다.
그러므로 사이클로이드의 궤적은 ( r*(θ-sinθ), r*(1-cosθ))라고 깔끔하게 나온다. 원이 헛돌지 않고 제대로 굴러가는 이상, 점이 아예 뒤로 후퇴하는 일은 어떤 경우에도 절대 없다는 걸 알 수 있다.
사이클로이드는 원이나 타원의 호와 비슷하게 생겼지만, 실제로는 이와 무관한 별개의 궤적이다. 아래의 그림 비교와 관련 설명을 참고하시라.
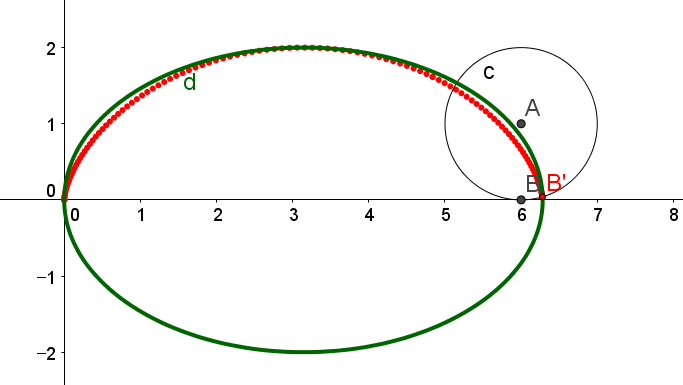 | 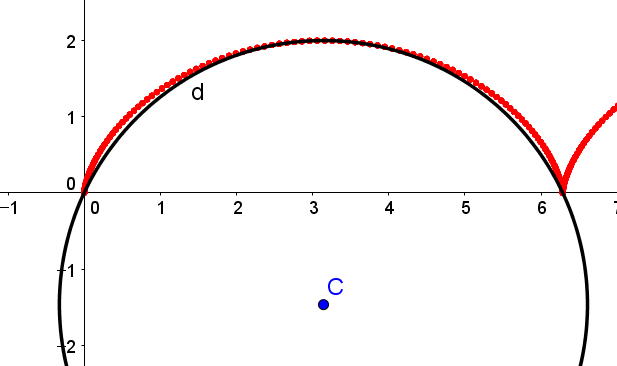 |
그리고 얘는 x와 y의 위치를 매개변수를 통해 제각기 나타낼 때는 식이 저렇게 아주 깔끔하게 구해지는 반면, y=f(x) 꼴의 단순한 양함수로 나타내는 건 굉장히 복잡하고 까다롭다. x축이 그냥 sin(t)가 아니라 t-sin(t)인데.. 이게 역함수를 구하기가 몹시 난감하기 때문이다.
그나마 x=g(y)라는 일종의 음함수에 가까운 형태로 나타내는 게 y=f(x)보다는 더 할 만하다. 원이 굴러간 거리에 대한 함수가 아니라 원의 범위 영역에 대한 함수 말이다.
사이클로이드는 이렇게 까다로운 면모가 있음에도 불구하고 한 사이클 궤적의 길이라든가 그 궤적 아래의 면적은 적분을 통해 깔끔하게 떨어지는 형태로 구할 수 있다. 이쪽으로 더 관심 있으신 분은 위키백과 등의 타 사이트를 참고하시라.
이 글에서 현수선 다음으로 사이클로이드를 소개한 이유는 얘도 현수선과 동급으로 역학적으로 아주 흥미로운 특성이 있는 물건이기 때문이다.
1. 최단 강하
먼저, 얘는 일명 ‘최단(최고속) 강하 곡선’이다. 높은 지점에서 낮은 지점으로 공을 굴리는데 무작정 최단 거리인 직선 경사로가 아니라, 사이클로이드를 상하 반전시킨 형태의 경사로를 만드는 게 좋다. 그러면 공이 중력 버프를 받아서 목적지에 더 빨리 도달하게 된다! (지면 마찰과 공기 저항 따위는 모두 무시)
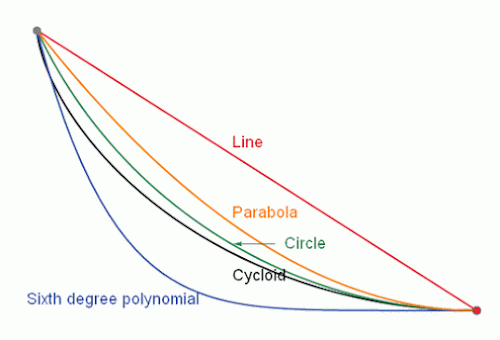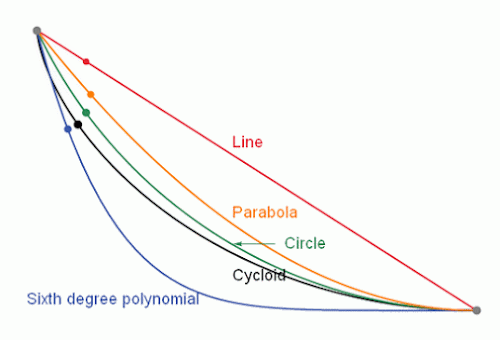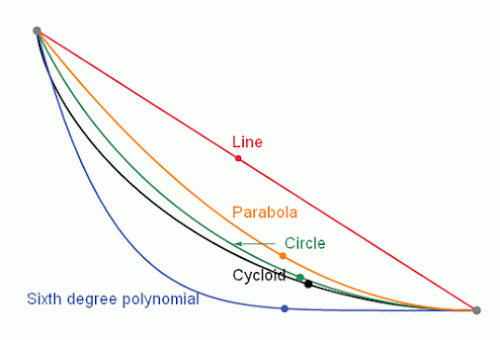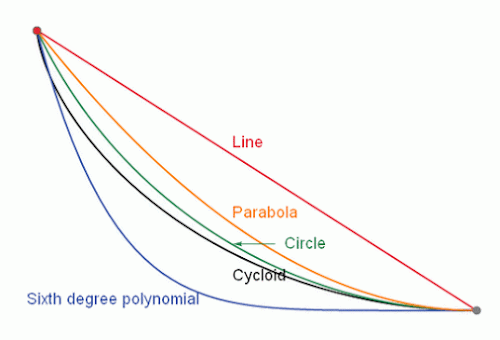
그렇다면 비행기의 비상 탈출용 미끄럼틀도 직선이 아니라 이런 형태로 만드는 게 더 나을 것 같다. 물론 현실적으로는 무리이겠지만, 그래도 어린이용 미끄럼틀 중에는 이런 과학 고증(?)을 반영하여 사이클로이드 곡선을 흉내 낸 모양인 것도 있다.
그런데 의문이 든다. 이것도 까놓고 말해 그냥 포물선이라든가, 사분원이나 2차 베지어 곡선, 혹은 아예 역학적인 안정성이 검증돼 있는 현수선이 최단 강하일 수도 있을 텐데 왜 하필 사이클로이드가 당첨인 걸까? 직선보다 아래로 볼록한 모양이어야 하겠다는 건 수긍이 가지만 왜 하필 저 모양이 최적인지는 직관적으로 납득이 잘 안 된다.
먼저 우리는 구슬이 처음 놓여 있는 좌측 최상단 꼭대기가 원점 (0, 0)이라고 가정하자. 그리고 계산의 편의를 위해, y축은 중력이 향하는 방향(=아래)이 +로 증가하는 방향이라고 간주하도록 하겠다. 즉, 통상적인 수학 좌표가 아니라 컴퓨터 화면의 좌표계를 사용한다는 것이다.
그러면 구슬은 아래로 굴러가면서 x축과 y축 모두 값이 일관되게 증가한다고 생각할 수 있으며, 저 사이클로이드 공식도 y축의 부호를 뒤집을 필요 없이 그대로 사용할 수 있다.
이 문제를 푸는데 매우 중요하게 활용되는 단서는 (1) "역학적 에너지 보존의 법칙"이다. 구슬이 직선 경사로를 쫙 구르건 그 어떤 꼬불꼬불한 곡선을 타고 오르내렸건, y축 중력 가속도가 g인 상태에서 y라는 높이만치 내려가 있다면 그 당시에 물체의 속도는 mgy = mv^2 /2를 근거로 v=sqrt(2*g*y)가 된다. 위치 에너지가 그만치 운동 에너지로 바뀌었음을 뜻한다. 당연한 말이지만 x축과는 전혀 무관하다.
이 속도는 xyz 같은 축을 총체적으로 고려한 단위 시간당 이동량이다. 그 속도를 얻은 상태에서 수평 이동을 한다면 구슬은 공기 저항과 마찰이 없는 한, 영원히 등속 운동을 할 것이다. 상승하면 속도가 점차 느려질 것이고, 하강하면 속도가 붙어서 빨라질 것이다.
여기까지 준비가 완료됐으면 사이클로이드 문제는 크게 두 방법으로 풀 수 있다.
하나는 뉴턴이 터를 닦으시고 오일러-라그랑주가 끝장을 낸 (2) 변분법을 동원하는 것이다. 하드코어한 고전역학의 범주에서 끝을 보는 것이다.
다른 하나는 파동 분야에서 정립된 (3) 스넬의 법칙을 접목하는 것이다. 겉보기로 수식의 압박이 변분법보다는 '약간' 덜할지 모르지만, 그럼 스넬의 법칙은 왜 어째서 성립하는지를 일일이 따지고 든다면 난이도는 비슷하게 안드로메다로 치솟는다.
그럼 변분법 버전부터 먼저 살펴보도록 하겠다.
통상적인 미분이 함수의 극점을 구해서(= 도함수가 0) 특정 구간에서 함수의 최소/최대값을 구하는 데 쓰인다면, 변분법이란 범함수의 최소/최대값을 구하는 방법론을 말한다.
그럼 범함수란 무엇이냐? 프로그래밍에는 평범한 숫자나 객체가 아니라 함수 자체나 람다를 다른 함수의 인자로 넘겨주는 게 있다. 그것처럼 수학에도 함수를 받아들여서 스칼라 형태의 값을 되돌리는 함수가 있는데, 그걸 범함수(functional)라고 한다. 특정 함수가 특정 구간에서 미분 불가능한 지점의 개수.. 그런 것도 범함수의 일종이 될 수 있다.
변분법을 이용하면 두 점을 잇는 가장 짧은 경로가 직선인 이유처럼 공리 수준의 너무 당연해 보이는 것부터 시작해서..
둘레가 동일한 도형 중에 면적이 최대인 놈이 원의 형태가 되는 이유, 물방울· 비누 방울이나 잠수정이 전부 구형으로 만들어지는 이유(단위 면적당 압력 최소화) 같은 것도 다 수학적으로 엄밀하게 유도할 수 있다.
최단 강하 곡선 문제에서 우리가 구해야 하는 것은 길이나 면적 따위가 아니라 "도달 시간"의 최소값이다.
구슬이 위에서 아래로 굴러가는 궤적을 y = f(x)라는 함수로 나타낸다면, a라는 임의의 x축 지점에서 구슬의 진행 속도는 f(a)의 값으로부터 구할 수 있다. 속도는 앞서 공식을 구한 바와 같이 전적으로 y축에 의해서만 결정되고, y축의 값은 x축 대한 함수 f로부터 구할 수 있으니 말이다.
그렇다면 (2-1) 이 함수를 어째 잘 적분해서 f(x)라는 함수에 대해 구슬이 다 내려갈 때까지 걸리는 시간도 구할 수 있을 것이다.
이건 흔히 떠올릴 수 있는 상황은 아니다. 속도 함수를 적분해서 구하는 건 보통은 거리이기 때문이다. 시간에 대해 적분하면 끝이다. (예: 시속 100km로 2시간을 달린 거리는 200km)
그런데 반대로 소요 시간을 구하기 위해서는 반대로 함수 궤적의 거리가 주어져 있어야 한다. (예: 시속 100km로 300km를 달리는 데 걸리는 시간은 3시간) 그래도 이것도 적분이긴 하다.
앞서 sqrt(2*g*y)이라고 값을 구한 속도 v는 거리/시간, 즉 ds/dt라는 개념이다. 그런데 이 ds라는 건 역시 x 변화량 대비 y의 변화량을 거리화한 것이며, y 변화량은 곧 f(x)의 변화량과 같다. 그러므로 이것은 sqrt(1 + f'(x)^2 )로 나타낼 수 있다.
v = ds/dt 에서 sqrt(2*g*f(x)) = sqrt(1 + f'(x)^2 ) / dt 가 되고..
이 관계로부터 dt = sqrt(1 + f'(x)^2 ) / sqrt(2*g*f(x))이 된다.
오.. 그러므로 구슬이 구르는 궤적 함수가 f이고 중력 가속도는 g, 구슬이 다 구른 오른쪽 끝의 x축 지점이 a라 할 때, 구슬이 다 구르는 데 걸리는 시간 T는 다음과 같이 깔끔하게 구해진다.
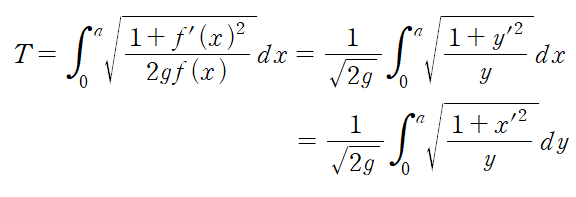
여기까지 도달했으면 문제가 반 정도는 해결됐다고 볼 수 있다. 우리는 a와 g가 고정돼 있을 때 T를 최소화하는 f(x)를 구하면 된다.
1/sqrt(2*g)는 그냥 상수이므로 적분 기호 밖으로 옮겨도 아무 상관 없다. 그리고 범함수에서는 그 정의상 x라는 변수뿐만 아니라 그 x에 대한 함수 f(x)까지 범함수의 parameter가 될 수 있다. 그렇기 때문에 f(x) 대신 그냥 y로 표기하며, 도함수도 f'(x) 대신 dy/dx라고 표기하는 걸 더 일상적으로 보게 된다. 애초에 사이클로이드도 f(x) 대신 x, y축 따로 매개변수 형태로 표기하는 게 더 유리하기도 하고 말이다.
이 문제를 풀기 위해 쓰이는 도구는 바로 (2-2) 오일러-라그랑주 방정식이다.
x, y라는 변수가 있고 F가 y, y', x에 대한 범함수라고 하자. 우리가 푸는 문제에서는 x, y는 구슬의 궤적을 나타내며, F는 그 궤적으로 끝까지 구르는 데 걸리는 소요 시간을 구하는 구간 적분이 된다.
오일러-라그랑주 방정식에 대해 제일 간단하고 엉성하게 요점만 말하자면, F가 극값(최소 또는 최대)이 나올 때 이들은 다음 등식을 만족한다.
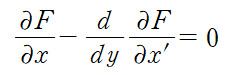
(왜 그런지 궁금하면 이변수함수의 연쇄법칙을 동원해서 저 식을 직접 유도하면 된다. 하지만 이 자리에서는 시간과 지면의 부족으로 증명을 생략하겠다. ㄲㄲ)
저 식에서 F에다가는.. 우리가 구한 처음 식 T에서 상수배 항과 dy 적분을 걷어낸 sqrt((1+x'^2)/y), 즉 순간 변화량을 대입한 뒤, 식을 x'에 대해 풀면 된다.
중요한 것은 우리의 경우, ∂F/∂x가 0이 보장된다는 것이다. 앞서 살펴보았듯이, 물체의 속도는 x축 위치와는 전혀 무관하고 y축 높이에 의해서만 결정되기 때문이다.
그러니 저 식에서 d/dy (∂F/∂x')도 같이 0이어야만 한다. F를 x'에 대해 편미분한 뒤, 양변에 sqrt(y)를 곱한 결과는 아래와 같이 된다. (x가 어떤 함수인지 정확한 정체를 모르기 때문에 x와 x'는 서로 독립변수로 간주됨) 이 식을 x'에 대해서 정리하면..
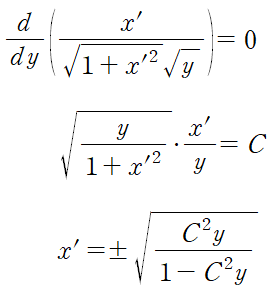
헥헥.. 이제 x'이 구해졌다. 그러면 함수 x는 y에 대해 적분을 해서 구할 수 있긴 하지만.. sqrt(x/(1-x))라는 함수는 부정적분을 호락호락 쉽게 구할 수 있는 놈이 아니다.
쟤를 수월하게 적분하는 방법은 x, y를 다른 변수 형태로 치환하는 것이다. 애초에 사이클로이드는 x, y 궤적을 매개변수 형태로 치환해야 표현하거나 취급하기 용이한 물건이다.
y를 sin(t)^2 / C^2 으로 치환하면 거추장스러운 C가 없어진다. 그리고 근호 안의 식이 sin(t)^2 / cos(t)^2로 바뀌고 근호도 없어져서 식 전체가 tan(t)로 바뀌는 마법이 펼쳐진다.
단, dy도 sin(t)^2의 도함수인 sin(t)*cos(t) dt로 바뀌기 때문에 저 tan(t)에다가 sin(t)와 cos(t)를 곱해 줘야 한다.
tan은 sin/cos이므로 cos는 서로 약분되어 없어지고.. 최종적으로 적분해야 하는 식은 sin(t)^2 dt가 된다.
그리고 sin(x)^2은 삼각함수 덧셈 정리로부터 유도된 반각 공식에 의거하여 (1-cos(2x))/2로 처분 가능하다. 이게 적분하기 훨씬 더 편하다.
사이클로이드를 기술하는데 각도가 t건 2t건 그건 중요하지 않으므로 x축의 궤적은 각도 θ에 대해 C*(θ-sin(θ))가 도출되며, y축은 이미 sin(t)^2의 간소화형인 C*(1-cos(θ))로 답이 나와 있다. 이것으로 유도 끝..
우리는 사이클로이드의 x, y축별 매개변수식에서 아주 중요한 특성을 하나 주목하게 된다. 바로 매개변수 t에 대해서 x축의 궤적 함수는 y축 궤적 함수의 부정적분이라는 것이다! 반대로 y축의 궤적 함수는 x축 궤적 함수의 도함수이다. 애초에 이런 관계였구나..
이것은 사이클로이드를 매개변수가 아닌 양/음함수로만 기술할 때는 간파할 수 없는 특성이다. 그리고 이런 특성이 존재하기 때문에 사이클로이드의 x, y 궤적은 앞서 제시되었던 미분 방정식을 만족하고 해당 범함수에 대해 오일러 방정식을 충족하고, 최단 강하 곡선 역할까지 한다고 볼 수 있다.
이상이다. 현수선하고 뭔가 비슷한 구석이 있는 것 같으면서도 현수선을 분석하는 것보다는 확실히 더 어려운 것 같다..;; 현수선이 역학적으로 자연스럽고 안정된 궤적이라면, 사이클로이드는 좀 더 인위적이고 최적화된 듯한 느낌이 드는 궤적이다. 다만, 둘 다 중력이 있기 때문에 존재한다는 공통점이 있다.
얘는 중력이 작용하는 지표면에서 공을 몇 도로 던졌을 때 제일 멀리 날아가냐 하는 문제와도 비슷한 느낌이 든다. 삼각함수의 반각 공식이 쓰였다는 공통점도 있으니 말이다. 하지만 사이클로이드는 그것보다도 당연히 훨씬 더 복잡하고 난해하다.
글이 이것만으로도 너무 길어졌으니, 최단 강하 증명의 다른 풀이법 등 나머지 얘기는 다음 시간에 계속하도록 하겠다. =_=;;
Posted by 사무엘


