김 용묵의 절대공간 - 블로그

컴퓨터그래픽에서 벡터 그래픽의 반의어로 픽셀과 비트맵을 다루는 체계를 래스터 그래픽이라고 흔히 부른다. 종이가 아니라 해상도가 상대적으로 낮은 모니터 화면이 주 무대이고, 면을 채우는 기본 단위가 scan line(주사선)이라는 관점에서 정립된 용어이다.

그리고 2D 비트맵(더 정확한 명칭은 래스터..?) 그래픽 API를 보면 어떤 플랫폼용 어떤 언어의 라이브러리이든지 점과 직선, 곡선을 그리는 함수가 있고, 사각형과 원을 그리는 함수가 있다. 이게 기본이다.
점이나 사각형이야 그리는 방식이 너무 trivial하니 제끼고, 원이나 곡선을 빠르게 그리는 원리는 기하 알고리즘의 일종으로 다뤄지기도 한다. 그 단순한 직선조차도 굵기가 2픽셀 이상이 되면 중심점을 생각해야 할 것이고, 무거운 부동소수점 연산 없이 anti-aliasing까지 하면서 그린다는 조건이 추가되면 결코 쉽지 않은 일이 된다.

그리기 기능 중에서 특정 픽셀부터 시작하는 flood fill은 무척 독특한 동작이다. 기하 알고리즘이라기보다는 스택 메모리를 동원해서 컴에게 길 찾기 재귀호출 노가다를 시키는 코딩의 영역이다. 빼곡한 미로의 내부에 있는 한 점에서 flood fill을 시켜 보면 이건 본질적으로 길 찾기와 다를 바 없다는 걸 알 수 있을 것이다.

글쎄, flood fill은 그래픽 에디터에서 사용자가 내리는 채우기 명령을 구현하는 형태로나 쓰이지, 직선과 곡선, 사각형과 원처럼 그림을 그리는 구성요소로서 프로그램이 내부적으로 사용할 일은.. 정말 아주 특수한 상황이 아니라면 없을 것이다. 도형 자체를 처음부터 내부가 채워진 형태로 그려야지, 도형의 윤곽만 그린 뒤에 도형 내부의 임의의 점을 따로 주고 채우는 건 몹시 비효율적이기 때문이다.

그래서 그래픽 라이브러리에는 다각형을 그리는 함수가 있다. 다각형의 경계선만 찍찍 그리는 것이야 LineTo만으로 얼마든지 할 수 있으므로, 이런 함수는 내부가 채워진 다각형을 그리는 것이 핵심이다. 그러니 이 함수는 다른 함수와 달리, 반드시 다각형의 꼭지점들이 담긴 배열을 전달받아야 한다.
옛날 도스 시절의 베이식은 타 언어들에 비해 그래픽 모드의 접근성이 좋았지만, 정작 다각형을 그리는 API는 없었다.

그럼 다각형을 채우는 기능은 어떤 방식으로 동작하는 걸까?
이걸 구현하기 위해서는 어떤 점이 다각형의 내부에 속하는지를 판단해야 한다. 더 나아가서 이 점에서 한쪽으로 scan line을 그어 나갈 때 어디까지가 동일하게 다각형의 내부 또는 외부인지를 판단해야 한다.

이걸 판단하는 방법은 의외로 간단하다. 그 점으로부터 아무 방향으로(예: x축 양의 방향) 한없이 직선을 그을 때, 그 선이 다각형을 구성하는 선분과 얼마나 몇 번이나 마주치는지를 판단하면 되며, 이걸 판단하는 방법도 크게 두 갈래로 나뉜다. 바로 (1) 홀짝 아니면 (2) 0여부이다.

홀짝법은 마주친 선분이 짝수 개이면 다각형의 외부이고, 홀수 개이면 내부라고 판단한다. 다시 말하지만 이 가상의 선은 정말 아무 방향으로나 그리면 된다. 다각형이 모든 방향으로 닫혀서 내부에 공간이 존재한다는 사실 자체가 이 판별법의 correctness를 보장해 준다.

0여부는.. 홀짝보다 더 절묘하다. 초기값이 0인 가중치라는 걸 두는데, 마주친 선분이 우리가 그은 가상의 선을 위에서 아래로 교차한다면 가중치에 1을 더한다. 그렇지 않고 아래에서 위로 교차한다면 1을 뺀다.
이렇게 해서 최종적으로 가중치가 양수든 음수든 0이 아닌 값이 나온 점은 다각형의 내부라고 간주하고, 0인 점은 외부라고 간주한다.

0이나 홀짝이나 그 말이 그 말 같은데.. 실제로 자기네 선분끼리 배배 꼬아서 교차하지 않는 일반적인, 평범한 오목/볼록다각형이라면 어느 판별법을 사용하든 결과에는 아무 차이가 없다.
하지만 당장 오각형 별표를 한붓그리기로 그린 궤적을 줘 보면 둘은 서로 차이를 보인다.

Windows API에서는 SetPolyFillMode라는 함수가 있어서 두 방식을 모두 사용해 볼 수 있다. 더 단순한 홀짝법이 ALTERNATE이고 기본값이다. 0여부는 WINDING... Windows 1.x 시절부터 존재해 온 오래된 고전 API여서 그런지, 매크로 상수의 앞에 접두사가 붙어 있지도 않다(PFM_* 같은?? ㅎㅎ).

오각형 별표에서 별의 중앙에 생긴 공간을 보면.. 그 옆으로 다각형 경계를 나타내는 선이 어느 방향이든 두 개가 존재한다(짝수). 그런데 이들은 방향이 둘 다 오르막 아니면 둘 다 내리막이며, 이 때문에 winding value는 nonzero가 된다. 그러니 ALTERNATE일 때는 이 공간이 비워지지만 WINDING일 때는 공간이 채워지는 것이다.

그 위의 더 복잡한 꼬인 사각형도 상황이 비슷하다. 잘 살펴보면 이 궤적도 홀수점이란 게 전혀 존재하지 않으며 한붓그리기가 가능하다.
그런데 WINDING일 때는 궤적이 꼬여서 생긴 내부의 사각형 공간 둘 중에서 좌측 하단 한 곳만 채워져 있다. 그 이유는 역시 저기서만 winding value가 nonzero이기 때문이다.

일반적으로 WINDING(0여부)이 판정하는 다각형 영역은 ALTERNATE(홀짝)의 상위 호환이다. ALTERNATE가 판정하는 영역을 100% 포함하면서 일부 영역을 추가적으로 더 판정한다는 뜻이다. 그렇다고 해서 모든 닫힌 영역을 한 치의 예외 없이 몽땅 내부라고 판정하는 건 아니다.

뭐.. 현실의 벡터 그래픽에서 이 따위 선끼리 교차하는 배배 꼬인 폴리곤을 생성하는 것은 애초부터 권장되지 않는 금지 사항이다. 가령, 속이 빈 오각별을 그리고 싶으면 저렇게 보이는 대로 삼각형 다섯 개로 풀어서 표현하라는 것이다. 윤곽선 폰트 등 벡터 그래픽 편집기들은 그렇게 폴리곤의 모양을 자동으로 수정해 주는 기능도 제공한다.
그러니 이렇게 fill mode의 차이점을 미주알고주알 관찰할 일이 현업에서는 거의 없을 것이고, 이런 건 그냥 학교에서 컴퓨터그래픽스 기초를 공부할 때 이런 방식도 있다는 걸 알기만 하고 넘어가면 될 것 같다.

하지만 그게 전부가 아니다. 다각형 채우기의 기능이 더 확장되면 다음 영역에도 도달하는데, 이때 fill mode의 차이점이 다시 드러나게 된다.

1. 여러 다각형을 한꺼번에 그리기
이건 내부에 구멍이 뚫린 다각형을 그릴 수 있다는 것에 의의가 있다. 구멍은 Polygon 함수를 연달아 호출하는 것으로는 표현할 수 없기 때문이다.

Windows에는 여러 다각형을 한꺼번에 그리는 PolyPolygon이라는 함수가 있다. 그런데 아까처럼 한 다각형에서 변들이 서로 교차하고 꼬였을 때뿐만 아니라, 변은 꼬이지 않았고 여러 다각형들의 영역이 서로 겹칠 때에도 fill mode의 차이는 유의미한 동작의 차이를 만들어 낸다.

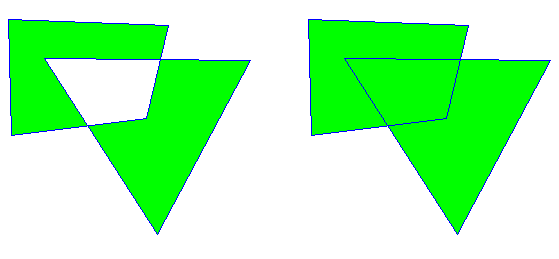
위의 그림은.. 뭐 이론적으로는 한붓그리기가 가능하기 때문에 역시 꼬인 단일 다각형으로 궤적을 나타낼 수 있다. 하지만 앞서 예를 들었던 오각별이나 그 사각형 그림과 달리, 일부 점과 점이 겹치는 건 피할 수 없을 것이다. 무슨 말인가 하면, 저 궤적을 꼭지점 좌표의 배열로 기술했을 때, 4개의 선분과 만나는 점은 두 번 등장하는 부분이 생긴다는 것이다.

꼬인 단일 다각형이 아니라 영역이 일부 겹치는 사각형과 삼각형을 서로 떼어서 PolyPolygon으로 그린 경우.. ALTERNATE(홀짝)에서는 짝수 개의 다각형에 속하는 영역은 비우고, 홀수 개에 속하는 영역만 칠한다. 그러고 보니 동작이 뭔가 XOR스러워 보인다. 각 다각형들의 꼭지점이 기술된 방향은 어느 쪽이건 무관하다 (시계 or 반시계 방향)

그러나 WINDING(0여부)일 때는 그 특성상 방향이 같은 다각형들은 겹치더라도 영역을 모두 칠한다. 겉의 껍데기가 시계 방향이라면.. 그 안의 구멍은 반시계 방향으로.. 다른 방향으로 칠해져야 구멍이 비게 된다! 다시 말하자면, WINDING에서도 위의 그림의 왼쪽처럼 중앙이 비어진 그림을 그리고 싶다면 사각형과 삼각형의 좌표 방향이 서로 반대여야 한다.
꼬인 단일 다각형에서 fill mode의 차이점을 설명하는 프로그래밍 서적들이.. 다중 다각형까지 연계해서 동일 개념을 설명하는 경우는 내가 딱히 못 본 것 같다.

2. 직선뿐만 아니라 베지어 곡선까지 포함된 궤적의 내부를 채우기
위와 같은 구멍 감지에다가 곡선 지원까지 포함되면.. 이건 뭐 윤곽선 글꼴 래스터라이저가 번듯하게 완성된다. 물론 본격적인 폰트 엔진은 거기에다 작은 크기에 대비한 정교한 안티앨리어싱과 힌팅, 글꼴 글립 캐시, 더 나아가 복잡한 유니코드 문자 형태 분석까지 추가되는데 이것들 하나하나가 별개의 전문 영역일 정도이다.

FreeType 라이브러리는 그 중에서 제일 저수준인 그리기, 안티앨리어싱, 힌팅까지만 담당한다. 요즘 소프트웨어들은 글자 하나를 찍는 것도 겨우 8*16, 16*16 비트맵 글꼴 찍던 시절과는 차원이 다르게 더 복잡해져 있는 셈이다.
그건 그렇고.. Windows API에는 직선과 곡선이 포함된 도형을 한꺼번에 그리는 것은 윤곽선만으로 한정이다. PolyDraw라는 함수가 있다.

내부를 채우는 것은 한 함수로 지원되지 않으며, path라는 걸 써야 한다. 얘는 Windows GDI가 제공하는 강력한 벡터 그래픽 라이브러리로, 직선, 베지어 곡선, 원과 원호, 심지어 다른 트루타입 글꼴의 글립까지 몽땅 궤적으로 표현해서 한꺼번에 내부를 채울 수 있다. 구멍 처리도 물론 된다.
BeginPath (그리기) CloseFigure (그리기) EndPath 이런 식으로 말이다. 위의 1과 2를 모두 할 수 있다.

내 경험상 트루타입 폰트는 WINDING 방식으로 래스터라이징을 한다. 글꼴 글립을 그릴 때부터 제일 밖의 path는 시계 방향이고, 그 안의 구멍 윤곽을 기술하는 path는 반시계 방향이고, 구멍 안의 칠하는 영역은 또 시계 방향.. 이런 식으로 디자인을 해야 한다.

허나, 예전에 MS Office 2003 이하 버전에서 제공되던 클래식 WordArt는 이 원칙을 지키지 않고 트루타입 글꼴도 홀짝 ALTERNATE 방식으로.. 짝수 회 overlap 영역은 무조건 비웠던 것 같다.
그래서 composite glyph 형태로 표현되는 비완성형 한글 글꼴에서 글립이 겹칠 수 있는 복잡한 글자를 찍어 보면 저렇게 흰 부위 glitch가 발생하곤 했다. (아래 그림에서 ㅆ, ㅠ, ㅔ 부분 참고)

Office 2007 이상부터 제공되는 WordArt는 이 문제가 해결됐다. 그리고 아래아한글의 글맵시도 0여부 WINDING 방식으로 맞게 색칠을 하기 때문에 glitch가 발생하지 않는다.

그러고 보니.. MS Office는 지난 2007때부터 그래픽 엔진이 크게 바뀌었다. 워드아트의 글자 장식 기능도 리뉴얼 됐고 PowerPoint 같은 데서도 직통으로 사용 가능해졌는데, 정작 본가인 Word에서는 2003 이하의 클래식 워드아트가 제공됐다. 다음 버전인 Office 2010부터 Word에서도 동일하게 리뉴얼된 워드아트가 제공되기 시작했다.

Posted by 사무엘

등산 이야기만 몇 콤보로 계속되는 와중에 오랜만에 또 프로그래밍 얘기를 좀 하겠다.

본인은 예전에 열차나 건물(대표적으로 영화관)에서 좌석 배당 알고리즘이 어떻게 될까 궁금해하면서 이와 관련된 썰을 푼 적이 있다. 그리고 이와 비슷한 맥락에서, 점을 최대한 균등하게 순서대로 뿌리는 ordered 디더링의 가중치, 다시 말해 흑백 음영 단계 테이블은 어떻게 만들어지는 것일까 하는 의문을 제기했다. 그 당시엔 의문 제기만 하고 더 구체적인 해답을 얻지는 못했다.

그래픽 카드가 천연색을 표현할 수 있게 되면서 이제 컴퓨터에서 선택의 여지가 없는 '생존형'(?) 디더링의 필요성은 전무해졌다. 비디오보다는 아주 열악한 네트워크 환경에서 그래픽의 용량을 극도로 줄일 필요가 있을 때에나 특수한 용도로 제한적으로 쓰이는 듯하다. 색상뿐만 아니라 해상도도 왕창 올라가면서 이제는 글꼴의 힌팅조차 존재감이 많이 위태로워졌을 정도이니 세상이 참 많이도 변했다.

하지만 ordered 디더링이라는 건 점을 평면이나 공간에 최대한 골고루 질서정연하게 뿌리는 순서를 구하는 문제이다 보니, 계산 알고리즘의 관점에서는 실용적인 필요성과는 별개로 굉장히 흥미로운 문제인 것 같다.

(이제는 이런 무늬 패턴을 볼 일 자체가 거의 없어졌다..)

흑과 백이 정확하게 반반씩 있는 50% 경우를 생각해 보면, 당연한 말이지만 흑과 백은 대각선으로 엇갈린 형태로 존재한다. 수평선이나 대각선 형태가 아니다. ▤나 ▥가 아니라 ▩에 가까운 것이다.

그러므로 아주 간단한 2*2 크기의 음영이라면
(1 4)
(3 2)

가 된다. 수평선인 (1 2)(3 4)나 수직선인 (1 4)(2 3)이 아니라, (1 4)(3 2)라는 것이다.
그러니 태극기의 괘는 패턴이 (3 5)(4 6)이기 때문에 수직선에 가깝다. 그리고 이거 무슨 승용차에서 운전사가 있을 때와 없을 때, 좌석의 위치별로 상석에서 말석 순서 테이블과 비슷하다는 느낌도 든다.. -_-;;

시작점인 1은 언제나 좌측 상단으로 고정해서 생각해도 일반성을 잃지 않는다. 그럼 다음 2의 위치는 1에서 가장 멀리 떨어진 대각선이므로 역시 자동으로 결정된다.
그럼 (1 4)(3 2) 대신 (1 3)(4 2)는 불가능한 방향이 아니긴 하지만, 관례적으로 2 다음에 위쪽이 아니라 왼쪽에다가 3을 찍는 걸 선호하는 듯하다.

자, 그럼 얘를 조금 더 키워서 4*4 음영은 어떻게 될까?

(1 ? 4 ?) - (1 ? 4 ?) - (1 13 4 16)
(? * ? *) - (? 5 ? 8) - (9 5 12  8)
(3 * 2 ?) - (3 ? 2 ?) - (3 15 2 14)
(? * ? *) - (? 7 ? 6) - (11 7 10 6)

테이블의 크기가 딱 두 배로 커지면 새로운 숫자들은 언제나 기존 테이블의 틈바구니에 삽입된다. 그래야 균형이 유지될 수 있다.
각각의 틈바구니에 대해서 원래 칸의 대각선 아래 (+1, +1), 그리고 바로 아래 (0, +1), 바로 옆 (+1, 0)의 형태로 (5~8), (9~12), (13~16)이 매겨진다. 그랬더니 무슨 짝수 마방진 같은 복잡난감한 퍼즐이 채워졌다.

컴퓨터그래픽에서 실용적으로 가장 많이 쓰이는 음영은 8*8 크기이다. 모노크롬/16색 시절에 단색 패턴 채우기 함수들은 전부 8*8 패턴을 사용했다. 그러므로 얘는 음영을 64단계까지 표현할 수 있다.

8*8 패턴은 역시 4*4 패턴의 틈바구니에 삽입된다. 16 다음에 17이 들어가는 위치는 어디일까? 1과 2 사이에 5가 삽입되었던 것처럼 1과 5의 사이에 17이 삽입된다. 그리고 패턴 크기의 절반인 4픽셀 단위로 n, n+1, n+2, n+3이 (x,y), (x+4,y+4), (x,y+4), (x+4,y)의 순으로 번호가 매겨지는 건 변함없다.

거의 난수표 수준의 복잡한 테이블이 완성됐다. 규칙성이 뭔가 감이 오시는지? 그래픽 라이브러리들은 마치 삼각함수 테이블만큼이나 미리 계산된 디더링 테이블을 내장하고 있다.
그런데 이런 식으로 16*16 256단계 음영 테이블은 어떻게 만들 수 있을까?
각 구간을 순서대로 각개격파하는 게 아니기 때문에 분할 정복이나 재귀호출은 아닌 것 같다.

이런 숫자를 생성하는 코드를 작성하기 위해, 먼저 다음과 같은 변수들을 클래스나 전역변수 형태로 정의하자.

int mtrix[N][N]; int cs, ce;
static const POINT PTR[4] = {
    {0,0}, {1,1}, {0,1}, {1,0}
};

void Draw(int y, int x, int delta)
{
    for(int i=0;i<4;i++)
        mtrix[y+PTR[i].y*delta][x+PTR[i].x*delta]=ce++;
}

Draw는 특정 지점에서 n 간격으로 (0,0), (n,n), (0,n), (n,0)의 순으로 ce부터 ce+3까지 번호를 매겨 주는 역할을 한다.
이를 이용하면 2*2의 경우는 Draw(0, 0, 1)을 통해 간단히 만들 수 있다.

void Case2()
{
    cs=2; ce=1; memset(mtrix, 0, sizeof(mtrix));
    Draw(0, 0, 1);
}

앞서 살펴보았던 4*4는 이런 형태가 되고..

void Case4()
{
    cs=4; ce=1; memset(mtrix, 0, sizeof(mtrix));
    for(int a=0;a<4;a++)
        Draw( PTR[a].y, PTR[a].x, 2 );
}

더 복잡한 8*8은 Draw를 어떤 순서대로 호출해야 할지 따져보면 결국 규칙성이 도출된다.
그렇다. 2중 for문이 만들어지며, 16*16은 3중 for문이 될 뿐이다.

void Case8()
{
    cs=8; ce=1; memset(mtrix, 0, sizeof(mtrix));
    for(int a=0; a<4; a++)
        for(int b=0; b<4; b++)
            Draw(PTR[a].y + PTR[b].y*2, PTR[a].x + PTR[b].x*2, 4);
}

void Case16()
{
    cs=16; ce=1; memset(mtrix, 0, sizeof(mtrix));
    for(int a=0; a<4; a++)
        for(int b=0; b<4; b++)
            for(int c=0; c<4; c++)
                Draw(PTR[a].y + (PTR[b].y<<1) + (PTR[c].y<<2),
                    PTR[a].x + (PTR[b].x<<1) + (PTR[c].x<<2), 8);
}

바로 이것이 우리가 원하는 정답이었다. 식을 도출하고 보니 규칙은 허무할 정도로 너무 간단하다. n중 for문을 재귀호출이나 사용자 스택 형태로 정리하는 건 일도 아닐 테고.
이 정도면 평면이 아니라 3차원 공간을 점으로 촘촘하게 채우는 것도 생각할 수 있다. PTR 테이블은 (0,0,0), (1,1,1)부터 시작해서 정육면체의 꼭지점을 순회하는 순서가 되므로 크기가 8이 될 것이다.

그리고 참고로 8*8 음영 행렬은 아래의 코드를 실행해서 생성할 수도 있다.

int db[8][8];
for (int y = 0; y < 8; y++)
    for (int x = 0; x < 8; x++) {
        int q = x ^ y;
        int p = ((x & 4) >> 2) + ((x & 2) << 1) + ((x & 1) << 4);
        q = ((q & 4) >> 1) + ((q & 2) << 2) + ((q & 1) << 5);
        db[y][x] = p + q + 1;
    }

내가 처음에 for문을 써서 작성한 코드는 함수로 치면 일종의 매개변수 함수이다. (t에 대해서 x(t)는 얼마, y(t)는 얼마)
그런데 저건 그 매개변수 함수를 y=f(t) 형태로 깔끔하게 정리한 것과 같다. 식이 뭘 의미하는지 감이 오시는가?

이런 걸 보면 난 xor이라는 비트 연산에 대해 뭔가 경이로움, 무서움을 느낀다.
덧셈이야 "니가 아무리 비비 꼬아서 행해지더라도 까짓거 덧셈일 뿐이지. 결과는 다 예측 가능해" 같은 생각이 드는 반면, xor에다가 비트 shift 몇 번 하고 나면 도저히 예측 불가능한 난수 생성 알고리즘이 나오고 암호화/해시 알고리즘이 만들어지기 때문이다. 지극히 컴퓨터스러운 연산이기 때문에 속도도 왕창 빠르고 말이다.

2002년에 우리나라에서 열렸던 국제 정보 올림피아드에서도 'xor 압축'이라는 제출형 문제가 나온 적이 있다. 임의의 비트맵 이미지가 주어졌을 때, 이걸 사각형 영역의 xor 연산만으로 생성하는 순서를 구하되, 연산 수행을 최소화하라는 게 목표이다.

한 점에 대해서 가로/세로로 인접한 점 3개를 추가로 조사하여 흑백 개수가 홀수 개로 차이가 나는 점을 일종의 '모서리'로 간주하여 각 모서리들에 대해 plane sweeping하듯이 xor을 시키면 그럭저럭 괜찮은 정답이 나온다. 단, 이것이 이론적인 최적해와 동일하다는 것은 보장되지 않는다. 그렇기 때문에 문제가 제출형으로 출제된 것이다.

재미있는 것은 모서리 판정도 xor로 하면 간단하게 해결된다는 것이다.
(pt[x][y]==1)^(pt[x+1][y]==1)^(pt[x][y+1]==1)^(pt[x+1][y+1]==1) 같은 식. 이유는 조금만 생각해 보면 알 수 있다.

난 Bisqwit이라는 필명을 쓰는 이스라엘의 무슨 괴수 그래픽 프로그래머의 코딩 동영상에서 저 코드가 흘러가는 걸 발견하고 가져왔다. 흐음..;; Creating a raytracer for DOS, in 16 VGA colors 뭐 이런 걸 올려서 시청자들을 경악시키는 분이긴 한데, 물론 레알 16비트 도스용 Turbo C나 QuickBasic 컴파일러로 저런 걸 돌린다는 소리는 아니다. 그건 알파고 AI를 개인용 데스크톱 컴퓨터로 돌리는 것만큼이나 불가능한 일이니 너무 쫄지 않아도 된다. (VGA 16색인 건 맞지만 메모리와 속도는 그 옛날 기계 기준이 결코 아님.)

엑셀에다가 저 16*16 음영 테이블을 입력한 뒤, 수식을 이용해서 숫자 n을 입력하면 그에 해당하는 음영이 생성되게 워크시트를 만들어 보니 재미있다. 이번에도 흥미로운 덕질을 했다.

 

Posted by 사무엘

열차의 승차권을 구입하면 좌석은 어떤 식으로 배당될까?
객차 하나당 좌석은 차량에 따라 60~70개 정도가 있으며, 열차 한 편성은 일반실만 생각하더라도 최하 4량부터 시작하고 KTX의 경우 거의 15량에 가깝다. 수백 개의 좌석들은 어떤 순서와 원칙대로 승객에게 팔려 나갈까?

난 철덕후로서 그 알고리즘이 예전부터 굉장히 궁금했다. 여러분은 그렇지 않은가?

버스 정도면 그냥 아무렇게나 랜덤으로 배당해도 별 무리가 없을 것이다.
우등 고속버스는 가장 쉽다. 승차 정원부터가 30명이 채 안 되는 소규모인 데다, 좌석이 구조적으로 2개짜리와 1개짜리로 나뉘어 있으니 말이다.

단독 승객에게는 진행 방향 기준으로 오른쪽의 단독 좌석부터 먼저 배당해 주고, 그게 매진되거나 2인 승객이 있으면 2인 좌석을 준다. 상석인 맨 앞자리는 약간 나중에 팔리도록 다른 가중치를 부여하고, 반대로 최악의 자리인 맨 뒷자리는 최하위 우선순위로 팔리게 하면 될 것이다.

그러나 열차는 단순하게만 좌석을 배당해서는 대략 곤란하다.
1부터 n호차까지, 그리고 진짜 무식하게 1번부터 m호석까지 앞에서 뒤로 순서대로 꽉꽉 승객을 채워 넣어서 뒤의 객차는 텅 빈 채로 달리게 할 리는 없을 테고..

그렇다고 좌석을(특히 단독 승객) 완전 랜덤으로만 여기저기 들쭉날쭉으로 배당하면 좌석의 단편화(fragmentation)가 너무 심해진다. 그래서 승객이 얼마 타지도 않은 상태인데 이따금씩 타는 2인 이상의 다수 승객은 이어진 좌석을 못 구해서 서로 찢어져서 앉아야 하는 일이 벌어질 수 있다.

결국 본인이 추측하기로는 열차의 좌석 배당은 저 양 극단의 중간을 절충하는 방식으로 이뤄질 것 같다.
두세 개의 객차를 묶음으로 나눠서 한 묶음 안에서 좌석을 무작위로 배당한 뒤, 그 묶음의 좌석이 다 매진되면 다음 묶음으로 간다. 각 묶음은 1~3호차, 4~6호차, 7~9호차 같은 규칙으로 만들 수도 있고, 반대로 1, 4, 7호차와 2, 5, 8호차, 3, 6, 9호차 같은 규칙으로 만들 수도 있다.

그리고 각 객차 안에서는 전체의 50~60% 정도는 단독 승객이 무작위로 띄엄띄엄 앉을 수 있게 배려한다. 즉, 2개짜리 좌석이라도 한 자리에 단독 승객이 있으면 거기는 일단 건너뛰고 다른 빈 자리를 찾는다는 뜻이다. 그러나 나머지 자리는 가능한 한 2인 승객이 한꺼번에 찜할 수 있게 비워 두며, 한 객차의 좌석의 10~20% 정도는 마치 KTX 동반석처럼 4인 가족이 연속해서 앉을 수 있게, 가능한 한 1~2인 승객에게 금세 팔리지 않도록 비워 둔다.

단독 승객의 경우 창측 좌석이 내측 좌석보다 먼저 팔리게 하는 건 기본이다. 또한 열차에서는 출입문과 가까운 맨 앞이나 맨 뒤 좌석이 '안 좋은 자리'이므로 이것 역시 다른 좌석이 모두 팔린 뒤에 나중에 팔리게 해야 할 것이다.
단독 승객용 좌석과 2인 이상 승객용 좌석 영역을 정하는 것 역시 '엿장수 마음대로' 무작위로 하면 되며, 그 비율 역시 평소에 승차권이 팔리는 단위 통계를 근거로 합리적으로 정하면 될 것이다.

저런 균형적인 요소에 덧붙여 환승 동선도 고려 대상이 된다.
국내의 예를 들면 KTX 천안아산 역과 장항선 아산 역은 남쪽 끝에서 만난다. 그리고 KTX는 한 편성이 무려 400m가 약간 안 되는 매우 긴 열차이다. 그렇기 때문에 경부선 KTX를 타다가 천안아산 역에서 장항선으로 환승하는 승객은 부산 방면(하행) 열차의 경우 최대한 앞쪽 객차로 좌석이 배당되고, 서울 방면 열차는 뒤쪽 객차로 좌석이 배당된다. 지하철에서 환승을 빨리 할 수 있는 객차의 위치와 정확히 같은 개념이며, 한국 철도도 그 정도 센스는 이미 갖추고 있다.

이 정도면 내가 보기에 열차 좌석 배당 전략을 짜는 건, 마치 열차 시각표를 짜는 것에 필적하는 철도 영업 기술의 결정체가 될 수도 있을 것 같다.
현실성 있는 열차 운행 시각표를 짜기 위해서는 그 나라의 철도 인프라와 지형 특성, 차량 제원, 승객 패턴 등의 알토란 같은 영업 기밀이 총동원되어야 한다. 이런 걸 계획하는 건 인원을 더 투입한다고 신속하게 되는 게 아니며, 핵심 똘똘이 인력 한두 명이 다 도맡아 한다.

좌석 배당도 마찬가지일 거라는 말이다. 철덕이라면 반드시 정복해야 하는 분야 중 하나 되시겠다.
비행기는 무게 배분이(한쪽에만 승객 무게가 지나치게 쏠리지 않게) 좌석 배당에 감안되는 요인이라고 하는데, 철도는 무게 배분 걱정은 할 필요가 없는 대신 길다는 특성상 다른 변수가 존재하는 셈이다.

자, 여기까지만 글을 쓰려고 했는데, 빈 좌석에다 승객을 일정 규칙대로 채워 넣는 과정을 생각하자니 컴퓨터그래픽에서 중요하게 다뤄지는 알고리즘 분야가 문득 떠오르더라.
바로 디더링이다.

디더링은 적은 수의 색깔을 섞어서 더 화려한 색깔을 아쉬운 대로 표현하는 기법이다. 색을 물리적으로 섞을 수는 없으니 결국 서로 다른 색깔을 번갈아가며 늘어놔야 하는데, 한 색깔이 뭉치는 게 아니라 서로 다른 색깔들끼리 최대한 고르게 퍼지도록 픽셀을 배열해야 한다.

본인은 과거에 Windows 3.x 시절에 그림판에서 임의의 RGB 값을 주면 그 색을 16컬러만으로 디더링하여 표현하는 걸 보고 무척 신기해했었다. 가령, 흑에서 백으로 단계를 증가시킬 때, 검은색에서 흰색 점이 차츰 늘어나는 순서가 어떻게 정해지는지가 무척 궁금했다.

그 규칙을 디더링에서 threshold matrix라고 부른다. 일반적인 그래픽 프로그램에서는 8*8짜리를 사용한다. (출처는 위키백과) 저기서 1부터 16까지의 점을 순서대로 채우면 25% 음영이 그려지고, 32까지 채우면 흑백이 딱 반반씩 번갈아가며 등장하는 50% 음영이 되는 식이다.

처음에는 4픽셀 간격으로 띄엄띄엄 점을 그리고, 나중에는 그 사이의 4픽셀 간격을 채우는 식으로, 점들이 뭉치지 않고 어떤 경우에도 최대한 흩어져서 퍼져 있게 한다. 임의의 격자 크기가 주어졌을 때 threshold matrix를 생성하는 프로그램을 만들 수도 있을 법해 보이는데 그리 만만한 일은 아닌 것 같다. 마방진도 아니고 말이다.

더 나아가 임의의 색을 16컬러 디더링 패턴으로 표현해 내는 프로그램을 직접 짜 보면 어떨까? 주어진 색을 가장 가깝게 표현할 수 있는 2색 또는 3색 조합을 구한 뒤, 그 비율만큼 threshold matrix를 각각의 색으로 채우면 될 것이다. 색조합을 구하는 것은 미지수의 개수가 식의 개수보다 더 많아서 답이 하나로 딱 떨어지지 않는 부등식이 될 터이니, LP(선형 계획법) 같은 계산 기법이 동원돼야 하지 않을까 싶다.

그렇게 threshold matrix만을 정석대로 적용하면 ordered dithering이 된다. 그러나 그것만으로는 그림이 칙칙하고 보기가 안 좋기 때문에, 디더링된 색깔의 픽셀이 인접 픽셀에 시각적으로 끼치는 영향을 감안하여(error diffusion) 더 정교하게 디더링을 수행하는 알고리즘이 실생활에서 쓰인다. 더 깊게 들어가는 건 이 글의 범위를 벗어나므로 자세한 설명을 생략하겠다.

뜬금없이 디더링 얘기를 꺼낸 이유는.. 저렇게 디더링 점을 찍어 나가는 게 마치 열차 좌석을 배당하는 것과 비슷한 심상이 느껴져서이다. 열차 좌석의 점유 여부를 흑백 픽셀로 표현하고 시간이 흐름에 따라 픽셀들의 상태를 표시하는 시뮬레이션을 돌려 보면 재미있을 것 같다. 한쪽은 검은 색이 듬성듬성 있고, 한쪽은 검은 색이나 흰 색이 좀 연속해서 있겠지 아마?

철도의 좌석 배당 알고리즘과 래스터 그래픽의 디더링 알고리즘은 서로 따로 생각하고 있었던 주제인데 이렇게 한 글로 연결이 됐다. 마치 예전에 내가 열차의 급행 등급과 셸 정렬을 한데 묶어서 글을 썼듯이 말이다. 참 신기한 일이 아닐 수 없다. ㅋㅋㅋㅋ

Posted by 사무엘

요 그림이 고등학교 수학 II에서 배우는 진정한 묘미 중 하나입니다.

(0, 0), (x, 0), (0, y)의 직각삼각형을 원점을 축으로 θ만큼 돌리니까 원점은 그대로고 밑변은 (x cosθ, x sinθ)가 됩니다.
그런데 밑변보다 y만치 위로 떠 있던 점은, 회전 과정에서 가로로는 높이 y의 sin값만치 “감소”(왼쪽으로)하고, 세로로는 cos값만치 증가합니다.

그러니 (x cosθ - y sinθ, x sinθ + y cosθ)의 형태가 되는데, 이는 원래 점인 x, y에 대한 일차변환으로 일반화할 수 있습니다. 결국

(cosθ, -sinθ)
(sinθ,  cosθ)

가 됩니다. “꼬마신 신꼬”라고 외우는 그 유명한 회전변환 행렬입니다.
이걸 모르면 특히 컴퓨터그래픽에서 현란한 벡터 조작이나 3차원 그래픽 같은 건 상상도 할 수 없습니다.

이 행렬식의 값은 1 (임의의 각도의 cos 제곱과 sin 제곱의 합은?), 따라서 이렇게 도형을 일차변환 시키더라도 원래 도형의 넓이를 바꾸지 않는다는 걸 알 수 있습니다. 역행렬은 sin 쪽 부호만 맞바꾸면 됩니다. 기하학적으로, 상식적으로, 역행렬 공식에 맞춰 생각해도 전부 명확합니다.

공통수학에서는 삼각함수란 게 있다는 것, 그리고 한 삼각형의 세 변과 세 각이 주어졌을 때 삼각함수가 이런 특성을 갖는다는 것을 배웁니다. 기하학인지 대수학인지 감을 못 잡는 이 괴상한 함수는 흥미보다는 학생들에게 어마어마한 암기를 강요하면서 악몽 같은 기억으로 남아 있을 것 같습니다.

그러다가 수학 II로 오면서 단순히 삼각형과 관련된 것이 아닌 삼각함수 자체의 특성을 더 깊게 공부하게 됩니다. 이 회전행렬은 삼각함수의 덧셈 정리를 유도시킵니다.
특히, 저 행렬에다가 회전 행렬과 같은 각인 (cosθ, sinθ) 열벡터를 뒤에 곱해 주면 cosθ와 sinθ 값으로부터 cos 2θ, sin 2θ의 값을 얻을 수 있게 되고, 그 값으로는 아예 cos²θ, sin²θ의 값도 구할 수 있게 됩니다.

  cos 2θ = cos²θ - sin²θ,  cos²θ = (cos 2θ + 1)/2
  sin 2θ = 2 cosθ sinθ

공을 공중을 향해 몇 도로 던져야 가장 멀리 날아가는지를 삼각함수를 계수로 하는 이차방정식으로 풀어 보면, 결국 cosθ sinθ 값(곱)을 최대로 하는 θ 값을 구하는 문제로 귀착됩니다. 이는 sin 2θ의 값을 최대화하는 것과 같으므로 θ는 45도임이 명확해집니다.

sin과는 달리 cos은 양 함수의 제곱의 합으로 바뀐다는 점도 흥미롭습니다. 2θ보다 더 일반적인 α와 β의 경우를 생각해 보면 더욱 흥미로운 결과가 나오는데요, 덧셈 대신 두 각의 차이를 나타내는 뺄셈만을 예로 들어 보겠습니다.

  cos(α-β) = cosα cosβ + sinα sinβ
  sin(α-β) = sinα cosβ - cosα sinβ

cos을 보면 이는 정확하게 벡터 내적과 관련이 있음을 알 수 있습니다. x, y 성분인 벡터를 거리와 각도로 바꿔서 표현해 보면, Ax·Bx + Ay·By가 왜 |A||B| cosθ인지가 명확해집니다. 공통수학 때 배운 코사인 제 2법칙과도 이미 관련이 있고요.
cos은 90도일 때 0이 되기 때문에 두 벡터가 기하학적으로 직각인지 판단할 때 유용히 쓰일 수 있습니다. 부호가 갈리는 기점이 직각이죠. 시계에서 3시를 향하고 있는 벡터가 있다면, 5시나 1시를 향하는 벡터와는 양수이고, 7시나 11시 벡터와는 음수가 되는 셈입니다.

그럼 sin은 무슨 관련이 있는 걸까요? sin은 90도가 아닌 0도를 기점으로 부호가 바뀝니다. 3시를 향하는 벡터 기준으로 5시나 7시를 향하는 벡터의 부호가 서로 같고, 1시, 11시 벡터와는 서로 다릅니다.
정보 올림피아드 대비하여 기하 알고리즘 공부할 때, 특히 convex hull 같은 거 구할 때 단골로 등장하는 게 세 점이 시계 방향인지 반시계 방향인지 판단하는 공식인데요, 그게 바로 sin과 관련이 있습니다. Bx·Ay - By·Ax입니다. 이 식은 두 벡터가 일직선상에 있을 때 값이 0이 됩니다.

그러나 cos 계열인 벡터의 내적은 sin과는 달리 3차원 이상에서도 일관되게 구하는 공식이 있고 임의의 차원에서도 의미를 갖는다는 점에서 더욱 의미 깊다고 할 수 있습니다. 시계 방향 여부는 2차원 평면에서만 의미를 가지며, sin과 관련이 있는 벡터의 외적 역시 3차원 공간에서만 정의됩니다.

이렇게 한바탕 수학 II 초· 중반에서 홍역을 치른 삼각함수는 나중에 아예 sin(x)/x의 0 극한을 구하고 삼각함수를 미· 적분함으로써 더욱 해석학적으로 접근하게 됩니다. 고등학교 수학 교육 테크트리에서 맨 마지막으로 지어지는 최고급 건물 내지 유닛은 단연 미적분이라 할 수 있습니다.

Posted by 사무엘

컴퓨터는 배열로 표현된 직사각형 형태의 데이터를 처리하는 걸 좋아하며, 이는 그래픽에서도 예외가 아니다.
그러나 사람이 생각하는 개념을 그래픽 개체의 형태로 표현하다 보면 직사각형이 아닌 임의의 모양의 그래픽을 찍어야 할 일이 생긴다.
게임에서는 스프라이트가 좋은 예이고, 굳이 게임이 아니더라도 GUI 환경에서는 아이콘이라든가 심지어 customized 마우스 포인터도 그런 부류에 속하는 그래픽이다.

이런 그래픽은 결국 큰 직사각형 안에서 투명색을 제외한 나머지 색상을 찍는 방법으로 처리하는데, 그 구체적인 테크닉은 역사적으로 아래와 같은 세 양상을 거치며 바뀌어 왔다.

1. 모노크롬이나 그에 준하는 저색상: 비트 연산

그림을 두 장 준비한다. 그리고 그 두 장을 화면에다 그냥 copy만 하는 게 아니라, 화면에 이미 있는 픽셀과 비트 연산을 하여 그 결과를 찍는다. 이것을 raster operation이라고 하는데, 비트 연산은 CPU-friendly한 작업이기 때문에 컴퓨터가 나름 빠르게 수행할 수 있다.

준비해야 하는 그림은,
찍어야 할 내용이 그려져 있고 배경은 '검은색'(0)으로 처리되어 있는 '원래 비트맵'과,
원래 비트맵하고는 정반대로 배경은 무조건 '흰색'(1)이고 내가 차지하는 스프라이트 영역은 '검은색'(0)으로 처리되어 있는 '마스크 비트맵' 이렇게 둘이다. 마스크 비트맵은 1 아니면 0만 있는 모노크롬이다.
(따라서 '원래 비트맵'만으로는 검은색이 배경인지 아니면 스프라이트가 실제로 차지하는 검은색인지 알 수 없다.)

화면에다가는 먼저 마스크 비트맵을 AND 연산으로 그린다. 원래 화면에 있던 픽셀이 X라면, 마스크에서 배경으로 처리된 픽셀은 X AND 1이므로 X가 그대로 남고, 0이면 0이 되어 검은색이 된다.
즉, 마스크 비트맵에 대한 AND 연산은, 스프라이트가 칠해져야 할 영역만 시꺼멓게 만드는 효과를 낸다.

그리고 다음으로 이 자리에다가 원래 비트맵을 XOR 연산으로 그린다.
0 XOR X = X이므로, 이 연산을 수행해 주면 화면이 0으로(특히 마스크 비트맵 AND 연산으로 인해 0이 된) 시꺼먼 곳은 원래 비트맵이 그대로 그려지고, 원래 비트맵이 0인 배경은 아무 변화가 생기지 않는다.

그림의 출처는 위키백과.
이로써 스프라이트가 멋있게 그려졌다.
도스용 게임 중에 <위험한 데이브>는 이런 초보적인 XOR 방식으로 스프라이트를 찍었기 때문에, 검은 배경이 아니라 두 스프라이트가 겹치면 화면에 잔상이 남곤 했다.

옛날 윈도우 9x 시절에.. 컴퓨터 메모리가 많이 부족해서 하드디스크 스와핑/thrashing이 일어나고 프로그램의 각종 아이콘들이 그려지는 게 눈에 보일 때는... 아이콘이 차지하는 영역이 먼저 시꺼매지거나 반대로 잠깐 하얗게 번쩍이는 걸 볼 수 있었다. 흠, 프로토스 건물도 소환이 끝났을 때 실루엣이 허옇게 번쩍이다가 원래 형태가 드러나는데...;; raster 연산을 더블버퍼링 없이 화면에다 바로 그리다 보니, 컴퓨터 속도가 느려졌을 때 그 중간 과정이 눈에 띄는 것이다.

검정에다가 원래 비트맵의 색을 합성할 때는 이론적으로 OR을 써도 되는데 XOR이 의도적으로 쓰이고 있다.
이는 XOR이 유용하기 때문이다. XOR 1은 비트를 반전시켜 준다는 특성상, XOR 연산으로 그린 그림은 거기에다 XOR을 한번 더 해 주면, 다른 곳에 영향을 주지 않고 자기가 차지하고 있던 영역에서만 완전히 지워진다.

XOR 연산은 컴퓨터의 입장에서는 매우 부담이 가볍기 때문에, 마우스 선택 영역을 나타내는 점선 사각형이라든가 창 크기를 조절하는 작대기처럼 수시로 업데이트를 해 줘야 하는 비주얼 효과를 나타낼 때 즐겨 쓰인다.
아니, 텍스트 블록이라든가 깜빡이는 커서(캐럿)조차도 반전 사각형이니까 XOR이다.

마우스 포인터도 XOR 연산이다. 텍스트 입력란을 뜻하는 I자(beam) 모양의 마우스 포인터는 검은색이 아니라 배경색에 대한 반전색이다. 마스크 비트맵 값을 0이 아닌 1로 둬서 배경을 지우지 않은 상태에서 XOR 비트맵도 1로 해 주면 배경색이 반전되는 효과가 난다. ^^;;

XOR 연산은 디지털 컴퓨터가 존재하는 한 그래픽에서 언제까지나 없어지지 않고 쓰일 방식이긴 하지만... 오늘날은 다소 촌스러운(?) 것으로 간주되고 있기도 한다. GPU님이 계시니 화면 비주얼을 굳이 CPU 친화적인 방법만 고집할 필요는 없는 듯. 그래서 요즘은 뭔가 선택 영역을 나타낼 때 알파 블렌딩을 동원하여 다 옅은 파란 배경 + 더블버퍼링으로 대체되는 추세이다. 화면 전체의 DC를 얻어와서 XOR 연산을 시키는 건 Aero 환경에서는 오히려 성능을 더욱 떨어뜨리는 짓이기도 하니 말이다.

2. 모노크롬 이상 16~256색 사이: 컬러 키(color key)

그 후 컴퓨터의 그래픽 카드의 성능이 향상되면서, 256색 시대가 열렸다. 256색은 팔레트 조작이라는 과도기적인 괴악한 개념을 도입한 걸로도 유명하다.
색깔이 적당히 많아졌기 때문에, 비트맵에서 256색 중 하나만 투명색으로 예약하여 쓰지 않고 나머지 색은 그대로 찍게 하는 방식이 유리하다. 마스크 비트맵 따위를 번거롭게 구비할 필요가 없다. 또한 256색은 RGB 값이 아니라 인덱스 기반 컬러를 쓰기 때문에, xor 반전 연산이 어차피 그렇게 큰 의미를 지니지도 않는다. (실제 색깔값이 반전되는 게 아니라 팔레트 인덱스 번호가 반전되기 때문)

256색 전용으로 유명한 gif 그래픽 파일이 이런 컬러 키를 지정하여 투명색을 지정할 수 있다.
윈도우 API에도 비트맵이나 아이콘의 (0, 0) 위치 픽셀을 투명색으로 간주하고 그려 주는 함수가 있으며, SetLayeredWindowAttributes 함수는 컬러 키를 지정하여 해당색을 투명하게 처리함으로써 non-rectangular 윈도우를 만드는 효과를 내어 준다. region을 만들지 않고도 동일한 일을 할 수 있다는 뜻이다.

3. 트루컬러: 알파 채널

투명색 처리의 최종 완전체는 바로 알파 채널이다. 이건 과거의 픽셀 raster operation과는 차원이 다르며, 컴퓨터가 빨라진 정도를 넘어 그래픽 가속을 위한 별도의 GPU까지 등장하면서 가능해진 궁극의 기술이다.
매 픽셀에다가 이분법적인 투명 여부가 아니라, 이 픽셀이 배경과 얼마나 짙게 오버랩될지 반투명 등급 자체가 추가로 들어간다. RGB에 이어 A까지, 가히 색깔의 4차원화인데, 기계 입장에서는 한 픽셀당 딱 정확히 32비트이니 처리하기에는 다행히 좋다.

256색을 초월한 천연색 그래픽에는 워낙 많은 개수의 색상이 쓰이기 때문에.. 그 중 딱 한 색깔에다가만 컬러 키를 부여하는 게 무의미하다. 그리고 마치 글꼴에도 안티앨리어싱을 하듯, 스프라이트도 경계가 배경색과 부드럽게 융합해야 트루컬러의 진정한 의미가 살아난다. 그래서 알파 채널이 필요한 것이다.

윈도우 98에서 알파 채널을 적용한 비트맵 찍기라든가 그러데이션을 한번에 처리하는 API가 처음으로 추가됐다. 프로그램의 제목 표시줄에 그러데이션 효과가 윈도우 98에서 처음 추가되었는데, 바로 이 API를 쓴 것이다.
그리고 윈도우 XP에서는 알파 채널이 적용된 확장 아이콘이 처음으로 도입되었고, GDI+는 그리기 기능에 전반적으로 알파 채널을 염두에 두고 설계되었다. 하지만 GDI의 기본적인 벡터 드로잉 함수는 그런 새로운 기술로부터 소외되어 있으니 안타까울 뿐.

윈도우 비스타는 48*48도 모자라서 아예 256*256 크기의 아이콘을 지원한다. XP 때부터 이제 아이콘 하나가 2~3만 바이트에 달하는 시대가 됐는데(윈도우 3.1 시절에는 1~2천 바이트.. -_-), 전통적인 ico는 bmp와 같은 '무압축 포맷'인지라 256*256 크기의 32비트 픽셀을 저장했다간 크기를 감당할 수가 없기 때문에, ico 포맷은 내부적으로 png 파일도 포함할 수 있게 구조가 확장되었다.
gif를 대체하는 새로운 이미지 포맷인 png는 알파 채널을 지원한다. 그 자그마한 아이콘 하나도 전문 그래픽 디자이너가 포토샵으로 만들어야 하는 시대가 도래한 지 오래이다.

윈도우 내부적으로는 아이콘과 마우스 포인터 파일은 거의 동일한 포맷으로 간주된다. 아이콘은 이미지 이미지 비트맵과 마스크 비트맵 이렇게 둘 들어있는 형태이며, 마우스 커서는 거기에다 센터 위치가 추가되고.. 애니메이션 포인터는 gif스럽게 프레임이 더 추가되겠구나.
알파 채널이 등장하면서 마스크 비트맵은 존재 가치가 상당수 퇴색하긴 했으나, 오늘날에도 고전 테마(XP의 Luna, 비스타의 Aero 따위가 없는)에서 아이콘을 찍을 때라든가 disabled 상태 같은 변형 상태를 찍을 때 참고 정보로 쓰이기 때문에, 완전히 필요가 없어진 것은 아니다.

요컨대 오늘날은 기술 발전의 정도에 따라 최소한 세 가지 형태의 투명색 표현 기법이 쓰이고 있는 셈이다. 흥미로운 사실이다.

Posted by 사무엘