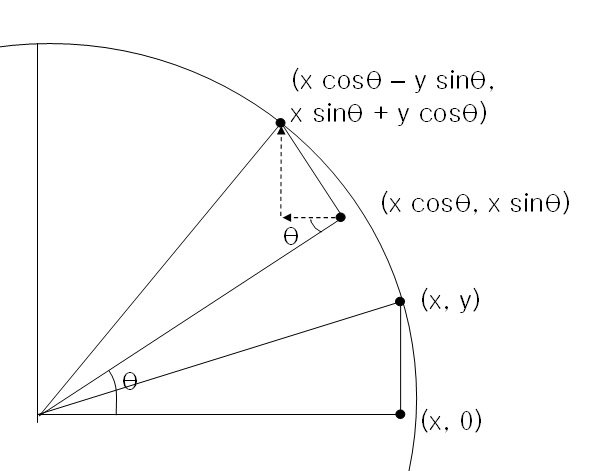
(0, 0), (x, 0), (0, y)의 직각삼각형을 원점을 축으로 θ만큼 돌리니까 원점은 그대로고 밑변은 (x cosθ, x sinθ)가 됩니다.
그런데 밑변보다 y만치 위로 떠 있던 점은, 회전 과정에서 가로로는 높이 y의 sin값만치 “감소”(왼쪽으로)하고, 세로로는 cos값만치 증가합니다.
그러니 (x cosθ - y sinθ, x sinθ + y cosθ)의 형태가 되는데, 이는 원래 점인 x, y에 대한 일차변환으로 일반화할 수 있습니다. 결국
(cosθ, -sinθ)
(sinθ, cosθ)
가 됩니다. “꼬마신 신꼬”라고 외우는 그 유명한 회전변환 행렬입니다.
이걸 모르면 특히 컴퓨터그래픽에서 현란한 벡터 조작이나 3차원 그래픽 같은 건 상상도 할 수 없습니다.
이 행렬식의 값은 1 (임의의 각도의 cos 제곱과 sin 제곱의 합은?), 따라서 이렇게 도형을 일차변환 시키더라도 원래 도형의 넓이를 바꾸지 않는다는 걸 알 수 있습니다. 역행렬은 sin 쪽 부호만 맞바꾸면 됩니다. 기하학적으로, 상식적으로, 역행렬 공식에 맞춰 생각해도 전부 명확합니다.
공통수학에서는 삼각함수란 게 있다는 것, 그리고 한 삼각형의 세 변과 세 각이 주어졌을 때 삼각함수가 이런 특성을 갖는다는 것을 배웁니다. 기하학인지 대수학인지 감을 못 잡는 이 괴상한 함수는 흥미보다는 학생들에게 어마어마한 암기를 강요하면서 악몽 같은 기억으로 남아 있을 것 같습니다.
그러다가 수학 II로 오면서 단순히 삼각형과 관련된 것이 아닌 삼각함수 자체의 특성을 더 깊게 공부하게 됩니다. 이 회전행렬은 삼각함수의 덧셈 정리를 유도시킵니다.
특히, 저 행렬에다가 회전 행렬과 같은 각인 (cosθ, sinθ) 열벡터를 뒤에 곱해 주면 cosθ와 sinθ 값으로부터 cos 2θ, sin 2θ의 값을 얻을 수 있게 되고, 그 값으로는 아예 cos²θ, sin²θ의 값도 구할 수 있게 됩니다.
cos 2θ = cos²θ - sin²θ, cos²θ = (cos 2θ + 1)/2
sin 2θ = 2 cosθ sinθ
공을 공중을 향해 몇 도로 던져야 가장 멀리 날아가는지를 삼각함수를 계수로 하는 이차방정식으로 풀어 보면, 결국 cosθ sinθ 값(곱)을 최대로 하는 θ 값을 구하는 문제로 귀착됩니다. 이는 sin 2θ의 값을 최대화하는 것과 같으므로 θ는 45도임이 명확해집니다.
sin과는 달리 cos은 양 함수의 제곱의 합으로 바뀐다는 점도 흥미롭습니다. 2θ보다 더 일반적인 α와 β의 경우를 생각해 보면 더욱 흥미로운 결과가 나오는데요, 덧셈 대신 두 각의 차이를 나타내는 뺄셈만을 예로 들어 보겠습니다.
cos(α-β) = cosα cosβ + sinα sinβ
sin(α-β) = sinα cosβ - cosα sinβ
cos을 보면 이는 정확하게 벡터 내적과 관련이 있음을 알 수 있습니다. x, y 성분인 벡터를 거리와 각도로 바꿔서 표현해 보면, Ax·Bx + Ay·By가 왜 |A||B| cosθ인지가 명확해집니다. 공통수학 때 배운 코사인 제 2법칙과도 이미 관련이 있고요.
cos은 90도일 때 0이 되기 때문에 두 벡터가 기하학적으로 직각인지 판단할 때 유용히 쓰일 수 있습니다. 부호가 갈리는 기점이 직각이죠. 시계에서 3시를 향하고 있는 벡터가 있다면, 5시나 1시를 향하는 벡터와는 양수이고, 7시나 11시 벡터와는 음수가 되는 셈입니다.
그럼 sin은 무슨 관련이 있는 걸까요? sin은 90도가 아닌 0도를 기점으로 부호가 바뀝니다. 3시를 향하는 벡터 기준으로 5시나 7시를 향하는 벡터의 부호가 서로 같고, 1시, 11시 벡터와는 서로 다릅니다.
정보 올림피아드 대비하여 기하 알고리즘 공부할 때, 특히 convex hull 같은 거 구할 때 단골로 등장하는 게 세 점이 시계 방향인지 반시계 방향인지 판단하는 공식인데요, 그게 바로 sin과 관련이 있습니다. Bx·Ay - By·Ax입니다. 이 식은 두 벡터가 일직선상에 있을 때 값이 0이 됩니다.
그러나 cos 계열인 벡터의 내적은 sin과는 달리 3차원 이상에서도 일관되게 구하는 공식이 있고 임의의 차원에서도 의미를 갖는다는 점에서 더욱 의미 깊다고 할 수 있습니다. 시계 방향 여부는 2차원 평면에서만 의미를 가지며, sin과 관련이 있는 벡터의 외적 역시 3차원 공간에서만 정의됩니다.
이렇게 한바탕 수학 II 초· 중반에서 홍역을 치른 삼각함수는 나중에 아예 sin(x)/x의 0 극한을 구하고 삼각함수를 미· 적분함으로써 더욱 해석학적으로 접근하게 됩니다. 고등학교 수학 교육 테크트리에서 맨 마지막으로 지어지는 최고급 건물 내지 유닛은 단연 미적분이라 할 수 있습니다.
Posted by 사무엘


