등산 이야기만 몇 콤보로 계속되는 와중에 오랜만에 또 프로그래밍 얘기를 좀 하겠다.
본인은 예전에 열차나 건물(대표적으로 영화관)에서 좌석 배당 알고리즘이 어떻게 될까 궁금해하면서 이와 관련된 썰을 푼 적이 있다. 그리고 이와 비슷한 맥락에서, 점을 최대한 균등하게 순서대로 뿌리는 ordered 디더링의 가중치, 다시 말해 흑백 음영 단계 테이블은 어떻게 만들어지는 것일까 하는 의문을 제기했다. 그 당시엔 의문 제기만 하고 더 구체적인 해답을 얻지는 못했다.
그래픽 카드가 천연색을 표현할 수 있게 되면서 이제 컴퓨터에서 선택의 여지가 없는 '생존형'(?) 디더링의 필요성은 전무해졌다. 비디오보다는 아주 열악한 네트워크 환경에서 그래픽의 용량을 극도로 줄일 필요가 있을 때에나 특수한 용도로 제한적으로 쓰이는 듯하다. 색상뿐만 아니라 해상도도 왕창 올라가면서 이제는 글꼴의 힌팅조차 존재감이 많이 위태로워졌을 정도이니 세상이 참 많이도 변했다.
하지만 ordered 디더링이라는 건 점을 평면이나 공간에 최대한 골고루 질서정연하게 뿌리는 순서를 구하는 문제이다 보니, 계산 알고리즘의 관점에서는 실용적인 필요성과는 별개로 굉장히 흥미로운 문제인 것 같다.
흑과 백이 정확하게 반반씩 있는 50% 경우를 생각해 보면, 당연한 말이지만 흑과 백은 대각선으로 엇갈린 형태로 존재한다. 수평선이나 대각선 형태가 아니다. ▤나 ▥가 아니라 ▩에 가까운 것이다.
그러므로 아주 간단한 2*2 크기의 음영이라면
(1 4)
(3 2)
가 된다. 수평선인 (1 2)(3 4)나 수직선인 (1 4)(2 3)이 아니라, (1 4)(3 2)라는 것이다.
그러니 태극기의 괘는 패턴이 (3 5)(4 6)이기 때문에 수직선에 가깝다. 그리고 이거 무슨 승용차에서 운전사가 있을 때와 없을 때, 좌석의 위치별로 상석에서 말석 순서 테이블과 비슷하다는 느낌도 든다.. -_-;;
시작점인 1은 언제나 좌측 상단으로 고정해서 생각해도 일반성을 잃지 않는다. 그럼 다음 2의 위치는 1에서 가장 멀리 떨어진 대각선이므로 역시 자동으로 결정된다.
그럼 (1 4)(3 2) 대신 (1 3)(4 2)는 불가능한 방향이 아니긴 하지만, 관례적으로 2 다음에 위쪽이 아니라 왼쪽에다가 3을 찍는 걸 선호하는 듯하다.
자, 그럼 얘를 조금 더 키워서 4*4 음영은 어떻게 될까?
(1 ? 4 ?) - (1 ? 4 ?) - (1 13 4 16)
(? * ? *) - (? 5 ? 8) - (9 5 12 8)
(3 * 2 ?) - (3 ? 2 ?) - (3 15 2 14)
(? * ? *) - (? 7 ? 6) - (11 7 10 6)
테이블의 크기가 딱 두 배로 커지면 새로운 숫자들은 언제나 기존 테이블의 틈바구니에 삽입된다. 그래야 균형이 유지될 수 있다.
각각의 틈바구니에 대해서 원래 칸의 대각선 아래 (+1, +1), 그리고 바로 아래 (0, +1), 바로 옆 (+1, 0)의 형태로 (5~8), (9~12), (13~16)이 매겨진다. 그랬더니 무슨 짝수 마방진 같은 복잡난감한 퍼즐이 채워졌다.
컴퓨터그래픽에서 실용적으로 가장 많이 쓰이는 음영은 8*8 크기이다. 모노크롬/16색 시절에 단색 패턴 채우기 함수들은 전부 8*8 패턴을 사용했다. 그러므로 얘는 음영을 64단계까지 표현할 수 있다.
8*8 패턴은 역시 4*4 패턴의 틈바구니에 삽입된다. 16 다음에 17이 들어가는 위치는 어디일까? 1과 2 사이에 5가 삽입되었던 것처럼 1과 5의 사이에 17이 삽입된다. 그리고 패턴 크기의 절반인 4픽셀 단위로 n, n+1, n+2, n+3이 (x,y), (x+4,y+4), (x,y+4), (x+4,y)의 순으로 번호가 매겨지는 건 변함없다.
거의 난수표 수준의 복잡한 테이블이 완성됐다. 규칙성이 뭔가 감이 오시는지? 그래픽 라이브러리들은 마치 삼각함수 테이블만큼이나 미리 계산된 디더링 테이블을 내장하고 있다.
그런데 이런 식으로 16*16 256단계 음영 테이블은 어떻게 만들 수 있을까?
각 구간을 순서대로 각개격파하는 게 아니기 때문에 분할 정복이나 재귀호출은 아닌 것 같다.
이런 숫자를 생성하는 코드를 작성하기 위해, 먼저 다음과 같은 변수들을 클래스나 전역변수 형태로 정의하자.
int mtrix[N][N]; int cs, ce;
static const POINT PTR[4] = {
{0,0}, {1,1}, {0,1}, {1,0}
};
void Draw(int y, int x, int delta)
{
for(int i=0;i<4;i++)
mtrix[y+PTR[i].y*delta][x+PTR[i].x*delta]=ce++;
}
Draw는 특정 지점에서 n 간격으로 (0,0), (n,n), (0,n), (n,0)의 순으로 ce부터 ce+3까지 번호를 매겨 주는 역할을 한다.
이를 이용하면 2*2의 경우는 Draw(0, 0, 1)을 통해 간단히 만들 수 있다.
void Case2()
{
cs=2; ce=1; memset(mtrix, 0, sizeof(mtrix));
Draw(0, 0, 1);
}
앞서 살펴보았던 4*4는 이런 형태가 되고..
void Case4()
{
cs=4; ce=1; memset(mtrix, 0, sizeof(mtrix));
for(int a=0;a<4;a++)
Draw( PTR[a].y, PTR[a].x, 2 );
}
더 복잡한 8*8은 Draw를 어떤 순서대로 호출해야 할지 따져보면 결국 규칙성이 도출된다.
그렇다. 2중 for문이 만들어지며, 16*16은 3중 for문이 될 뿐이다.
void Case8()
{
cs=8; ce=1; memset(mtrix, 0, sizeof(mtrix));
for(int a=0; a<4; a++)
for(int b=0; b<4; b++)
Draw(PTR[a].y + PTR[b].y*2, PTR[a].x + PTR[b].x*2, 4);
}
void Case16()
{
cs=16; ce=1; memset(mtrix, 0, sizeof(mtrix));
for(int a=0; a<4; a++)
for(int b=0; b<4; b++)
for(int c=0; c<4; c++)
Draw(PTR[a].y + (PTR[b].y<<1) + (PTR[c].y<<2),
PTR[a].x + (PTR[b].x<<1) + (PTR[c].x<<2), 8);
}
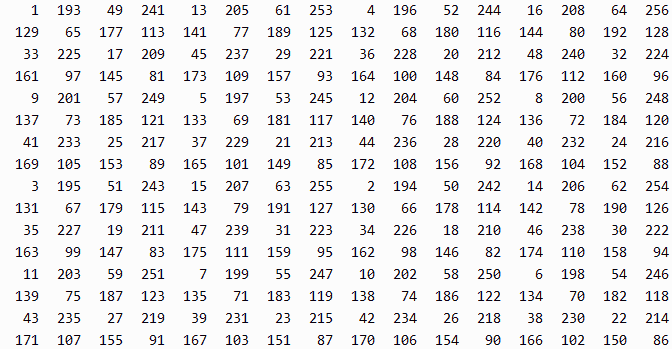
바로 이것이 우리가 원하는 정답이었다. 식을 도출하고 보니 규칙은 허무할 정도로 너무 간단하다. n중 for문을 재귀호출이나 사용자 스택 형태로 정리하는 건 일도 아닐 테고.
이 정도면 평면이 아니라 3차원 공간을 점으로 촘촘하게 채우는 것도 생각할 수 있다. PTR 테이블은 (0,0,0), (1,1,1)부터 시작해서 정육면체의 꼭지점을 순회하는 순서가 되므로 크기가 8이 될 것이다.
그리고 참고로 8*8 음영 행렬은 아래의 코드를 실행해서 생성할 수도 있다.
int db[8][8];
for (int y = 0; y < 8; y++)
for (int x = 0; x < 8; x++) {
int q = x ^ y;
int p = ((x & 4) >> 2) + ((x & 2) << 1) + ((x & 1) << 4);
q = ((q & 4) >> 1) + ((q & 2) << 2) + ((q & 1) << 5);
db[y][x] = p + q + 1;
}
내가 처음에 for문을 써서 작성한 코드는 함수로 치면 일종의 매개변수 함수이다. (t에 대해서 x(t)는 얼마, y(t)는 얼마)
그런데 저건 그 매개변수 함수를 y=f(t) 형태로 깔끔하게 정리한 것과 같다. 식이 뭘 의미하는지 감이 오시는가?
이런 걸 보면 난 xor이라는 비트 연산에 대해 뭔가 경이로움, 무서움을 느낀다.
덧셈이야 "니가 아무리 비비 꼬아서 행해지더라도 까짓거 덧셈일 뿐이지. 결과는 다 예측 가능해" 같은 생각이 드는 반면, xor에다가 비트 shift 몇 번 하고 나면 도저히 예측 불가능한 난수 생성 알고리즘이 나오고 암호화/해시 알고리즘이 만들어지기 때문이다. 지극히 컴퓨터스러운 연산이기 때문에 속도도 왕창 빠르고 말이다.
2002년에 우리나라에서 열렸던 국제 정보 올림피아드에서도 'xor 압축'이라는 제출형 문제가 나온 적이 있다. 임의의 비트맵 이미지가 주어졌을 때, 이걸 사각형 영역의 xor 연산만으로 생성하는 순서를 구하되, 연산 수행을 최소화하라는 게 목표이다.
한 점에 대해서 가로/세로로 인접한 점 3개를 추가로 조사하여 흑백 개수가 홀수 개로 차이가 나는 점을 일종의 '모서리'로 간주하여 각 모서리들에 대해 plane sweeping하듯이 xor을 시키면 그럭저럭 괜찮은 정답이 나온다. 단, 이것이 이론적인 최적해와 동일하다는 것은 보장되지 않는다. 그렇기 때문에 문제가 제출형으로 출제된 것이다.
재미있는 것은 모서리 판정도 xor로 하면 간단하게 해결된다는 것이다.
(pt[x][y]==1)^(pt[x+1][y]==1)^(pt[x][y+1]==1)^(pt[x+1][y+1]==1) 같은 식. 이유는 조금만 생각해 보면 알 수 있다.
난 Bisqwit이라는 필명을 쓰는 이스라엘의 무슨 괴수 그래픽 프로그래머의 코딩 동영상에서 저 코드가 흘러가는 걸 발견하고 가져왔다. 흐음..;; Creating a raytracer for DOS, in 16 VGA colors 뭐 이런 걸 올려서 시청자들을 경악시키는 분이긴 한데, 물론 레알 16비트 도스용 Turbo C나 QuickBasic 컴파일러로 저런 걸 돌린다는 소리는 아니다. 그건 알파고 AI를 개인용 데스크톱 컴퓨터로 돌리는 것만큼이나 불가능한 일이니 너무 쫄지 않아도 된다. (VGA 16색인 건 맞지만 메모리와 속도는 그 옛날 기계 기준이 결코 아님.)
엑셀에다가 저 16*16 음영 테이블을 입력한 뒤, 수식을 이용해서 숫자 n을 입력하면 그에 해당하는 음영이 생성되게 워크시트를 만들어 보니 재미있다. 이번에도 흥미로운 덕질을 했다.
Posted by 사무엘


